标签:clu 注意 一起 题目 有趣 ges detail 火柴棍 转移
如果对于一个平面图,将边看成火柴棍,将点看成用橡皮筋将木棍的头绑在一起(请自行脑补)。如果这个平面图不能够改变形状,称这个平面图为刚体图。
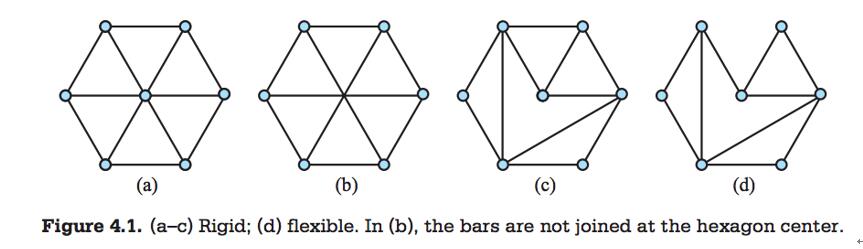
如下图中只有 D 不是刚体图。
给定一个 n*m 的方格图,你可以在某些方格的对角线上加支撑木棍以保持它的形状不变。
问让一个 n*m 的方格图变为刚体图,添加支撑木棍的方案数是多少?
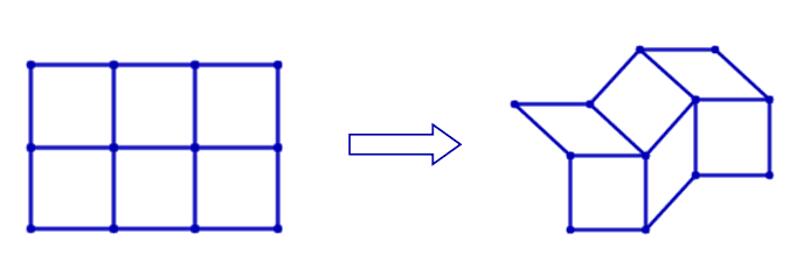
下图展现了一个 2*3 的方格图以及它不是刚体图的原因。
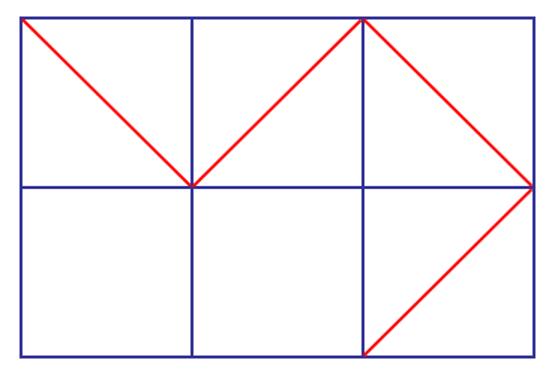
下图展现了一个让 2*3 的方格图变为刚体图的方案:
input
多组数据。每组数据只包含一行两个整数 n, m 描述方格图的大小
output
对于每组数据,输出方案数 mod 10^9 + 7。
sample input
1 2
3 2
7 9
10 10
sample output
4
448
357533852
935300639
自我脑补一下,可以发现一个正方形将它拖过来拖过去,也只能变成平行四边形。
即:无论怎么变化,它的对边始终平行。
相当于每一行的竖边的相对位置关系、每一列的横边的相对位置关系是确定的(即平行)。
考虑在一个正方形内加支撑,则它的横边与竖边就变为垂直的了。
又因为平行具有传递性,会将垂直关系传递。所以这个正方形所在的行的每一条竖边与所在的列的每一条横边垂直。
相当于一个正方形内加支撑,它所在的行与列就有了相对的位置关系。
不难发现方格图是刚体图与它所有的行与列互相之间都有相对的位置关系是等价的。
于是我们考虑以行、列建二分图,则相当于询问该二分图连通的方案数。
求连通方案很显然是容斥,即用总方案数减去不连通的数量。同时因为是二分图,所以可以不使用状压 dp 来做。
定义 dp[i][j] 表示左边 i 个点与右边 j 个点连通的方案数。
因为边有两类(对角线有两种),总方案数为 3^(i*j)。
再考虑不连通时与左边的点 1 连通的连通块,可得状态转移(注意左边的点 1 必须要选):
\[dp[i][j] = 3^{i*j}-\sum_{p\le i,q\le j}3^{(i-p)*(j-q)}*dp[p][q]*C_{i-1}^{p-1}*C_{j}^{q}\]
然后 O(n^4) 做个 dp 即可
#include<cstdio>
const int MOD = int(1E9) + 7;
const int MAXN = 10;
int dp[MAXN + 5][MAXN + 5], comb[MAXN + 5][MAXN + 5], pw[MAXN*MAXN + 5];
void init() {
for(int i=0;i<=MAXN;i++) {
comb[i][0] = 1;
for(int j=1;j<=i;j++)
comb[i][j] = (comb[i-1][j] + comb[i-1][j-1])%MOD;
}
pw[0] = 1;
for(int i=1;i<=MAXN*MAXN;i++)
pw[i] = 3LL*pw[i-1]%MOD;
for(int i=0;i<=MAXN;i++)
for(int j=0;j<=MAXN;j++)
dp[i][j] = pw[i*j];
for(int i=0;i<=MAXN;i++)
for(int j=0;j<=MAXN;j++)
for(int l=0;l<=i-1;l++)
for(int k=0;k<=j;k++) {
if( l == i-1 && k == j ) continue;
dp[i][j] = (dp[i][j] + MOD - 1LL*pw[(i-l-1)*(j-k)]*dp[l+1][k]%MOD*comb[i-1][l]%MOD*comb[j][k]%MOD)%MOD;
}
}
int main() {
int n, m; init();
while( scanf("%d%d", &n, &m) == 2 )
printf("%d\n", dp[n][m]);
}刚体。。。说实话我还真不知道是啥。。。
所以题意的理解卡了很久。。。
然后看到 n, m 这么小想可不可以写一个插头 dp 啥的,写着写着把自己 hack 掉了。。。
你告诉 n, m <= 10 然后跑一个 O(n^4) 的算法?这个数据范围。。。是用来误导人的嘛。。。
不过这个题的建模还是挺有趣。
标签:clu 注意 一起 题目 有趣 ges detail 火柴棍 转移
原文地址:https://www.cnblogs.com/Tiw-Air-OAO/p/11122815.html