标签:img col 路径 str span 二叉树 直接 流程 auto
直接进入正题:
一、如何从数组生成一个二叉树
假设数组为:{ 30, 13, 7, 43, 23, 12, 9, 33, 42, 21, 18, 6, 3, 50 },我们不对数组排序,直接生成二叉树。
创建流程:
1.将第一数作为根节点:
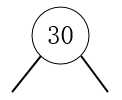
2.插入13,13小于30,放在30的左边子节点。
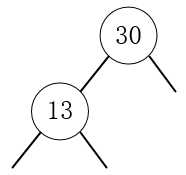
3.插入7,7小于30,7小于13,放在13的左边子节点。
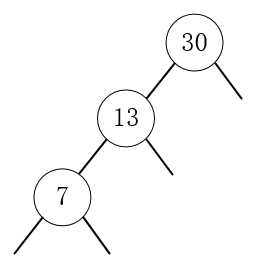
4.插入43,43大于30,放在30的右边子节点。
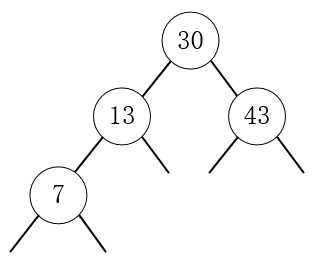
5.放入23,23小于30,23大于13,放入13的右边子节点。
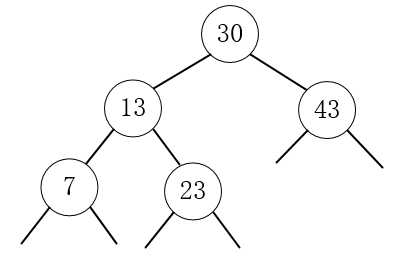
6.放入12,12小于30,12小于13,12大于7,放入7的右边子节点。
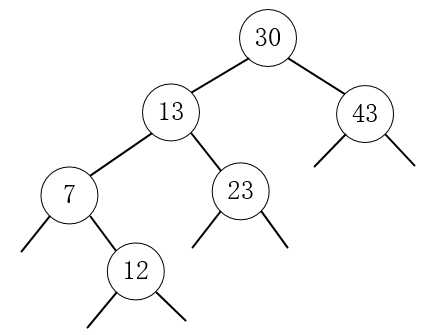
7.放入9,9小于30,9小于13,9大于7,9小于12,放入12的左边子节点。
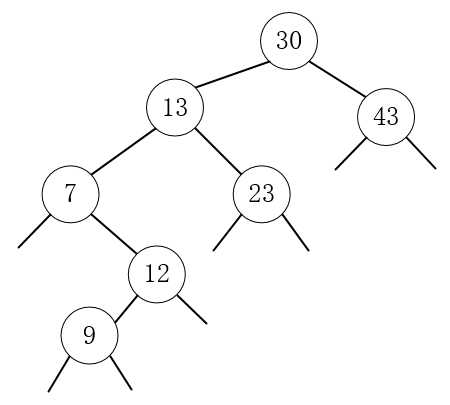
8.中间省略,最后生成的二叉树为如下:
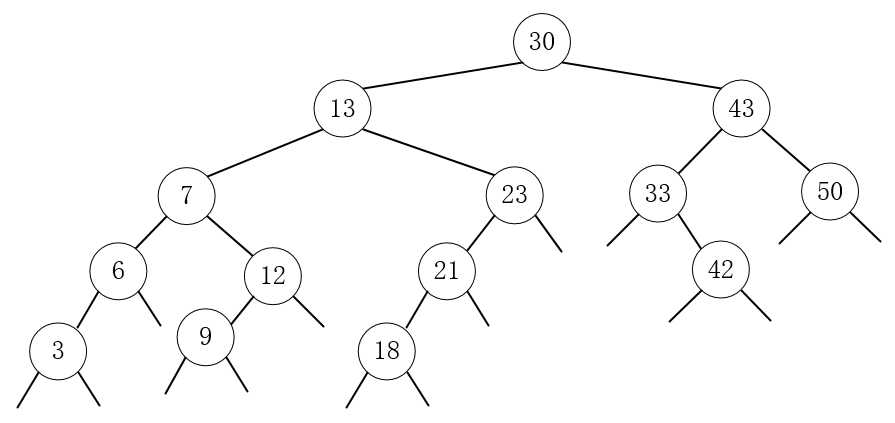
9.由上图可以看出,普通二叉树是不平衡的,最坏的情况可能会形成以下情况:
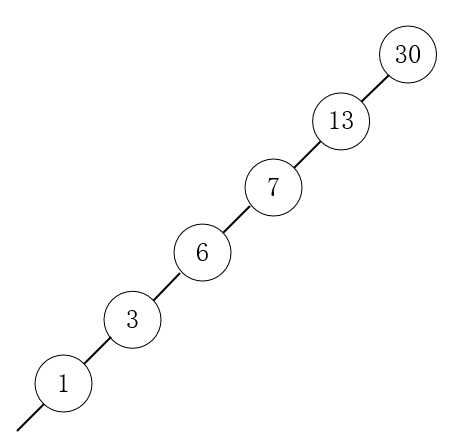
在这种情况下,当我们需要查找1的时候,时间复杂度就是O(n)。
普通二叉树的查找时间复杂度为[O(log2n),O(n)]之间。如果让其始终保持为O(log2n)的时间复杂度呢,我们就要创建平衡二叉树。
2-3树和红黑树都是平衡二叉树,我们先看2-3树,然后再由2-3树引出红黑树的原理。
二、平衡二叉树 2-3树
2-3树的意思就是,某个节点有两种可能:
一是正常的2-节点,包含一个值(或键),包含左右两个子节点。二是3-节点,包含两个值,包含左中右三个子节点。
如图所示:
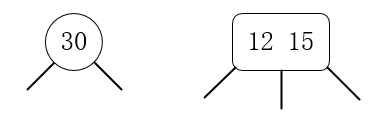
左边为2-节点,右边为3-节点。
向一个2-3树的节点中插入一个新的元素有以下几种基础操作:
1.插入一个比2-节点值小的元素,例如对值为30的2-节点插入20:
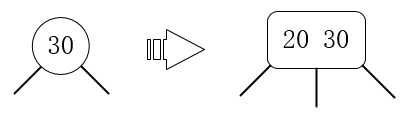
2.插入一个比2-节点值大的元素,例如对值为30的2-节点插入40:
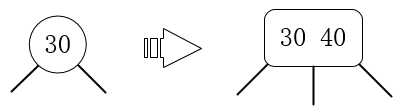
3.插入一个比3-节点左边值更小的值,例如对值为20 30的3-节点插入15:
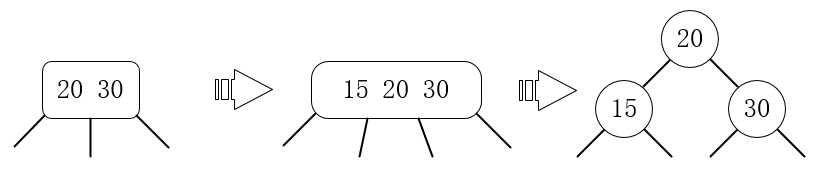
注意,这里对3-节点插入数据后,形成了一个4-节点,可以分解为最右边的二叉子树。
4.插入一个比3-节点左边值更大、比右边值更小的值,例如对值为20 30的3-节点插入25:
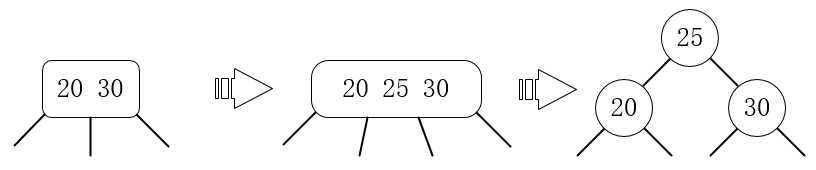
5.插入一个比3-节点右边值更大的值,例如对值为20 30的3-节点插入40:
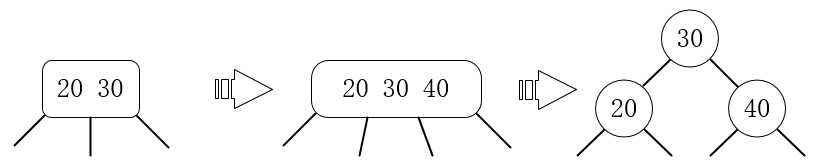
6.当下面一层的元素形成了4-节点,将4-节点的中间数往上层升级(分左右方向):
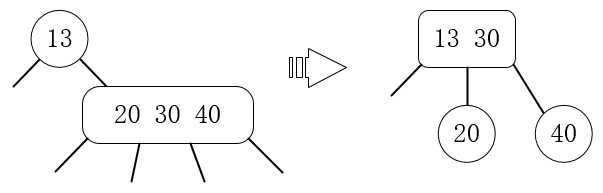
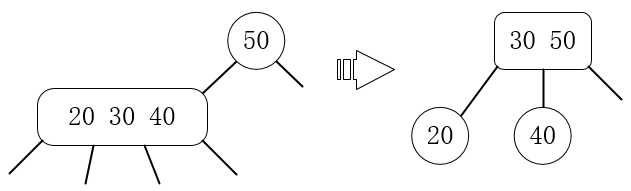
有了上述6个基本操作,我们开始使用前面的数组来创建2-3树:
数组为{ 30, 13, 7, 43, 23, 12, 9, 33, 42, 21, 18, 6, 3, 50 }。
创建流程:
1.将30作为根节点。
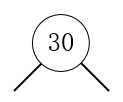
2.插入13,13比30小,形成一个值为13 30的3-节点。
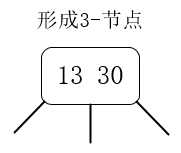
3.插入7,7比13小,形成一个值为7 13 30的4-节点,然后分解。
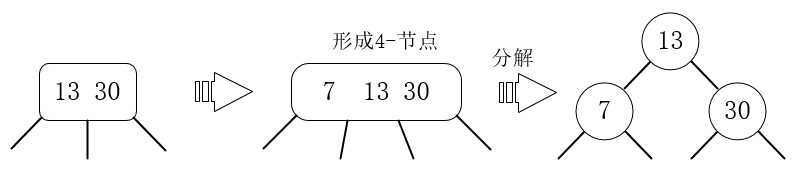
4.插入43,43大于13,43大于30,与30一起形成3-节点。
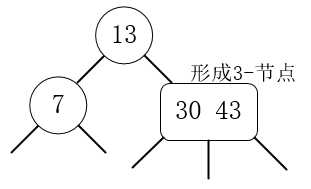
5.插入23,23大于13,23小于30,与30 43形成4-节点,然后分解。

6.插入12,12小于13,12大于7,与7组成3-节点
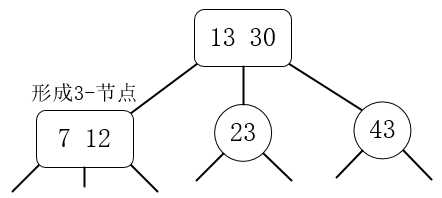
7.插入9,9小于13,9大于7,9小于12,与7 12组成4-节点,然后分解。分解后9升级到上一层,与13 30形成4-节点,再次分解。
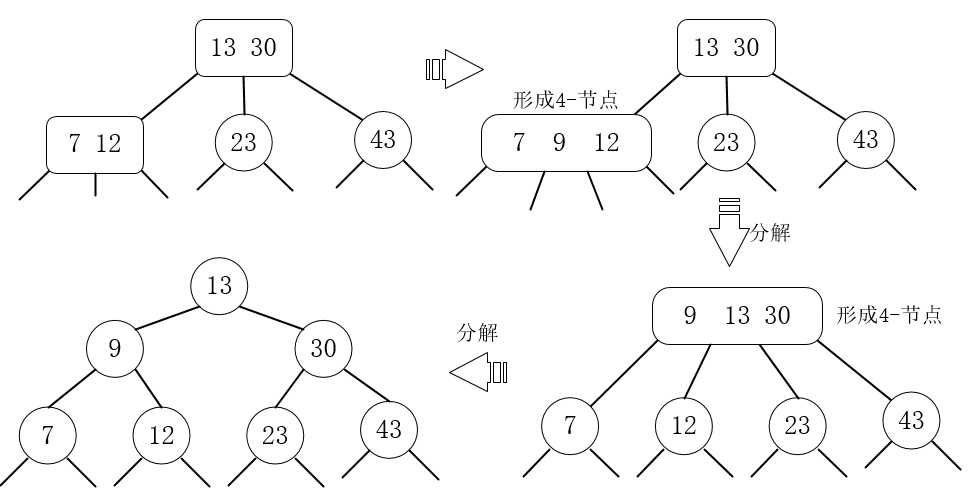
8.插入33,33大于13,33大于30,33小于43,与43组成3-节点。
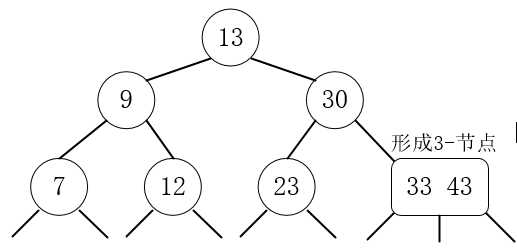
9.插入42,42大于13,42大于30,42大于33,42小于43,与33 43形成4-节点,然后分解。
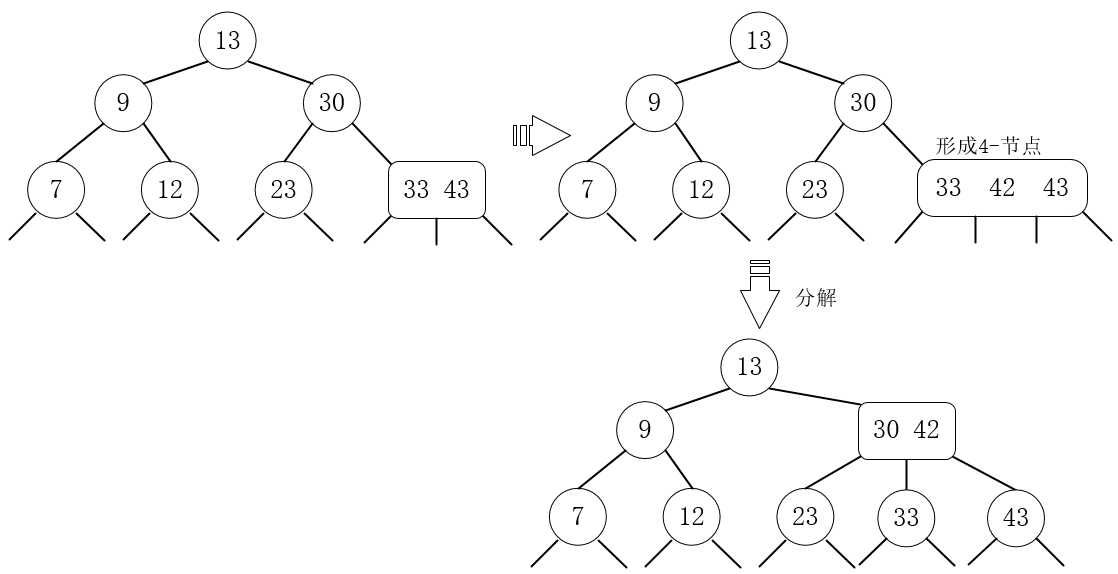
10.省略后面过程,最终生成结果为:
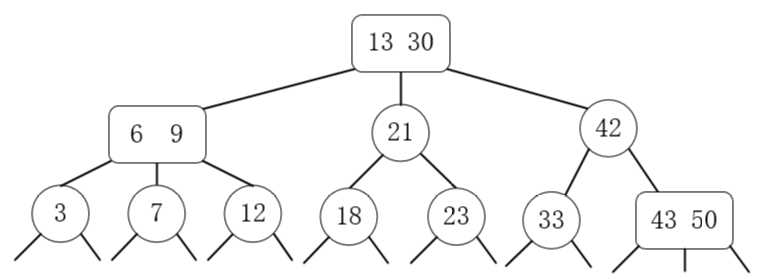
至此,我们创建了一颗2-3树,可以看出2-3树的平衡性还是很好的。
得到2-3树以后,我们可以将其进行结构上的一些变化:
1.将其中的所有3-节点,变换为以下形状,以左边子树为例:
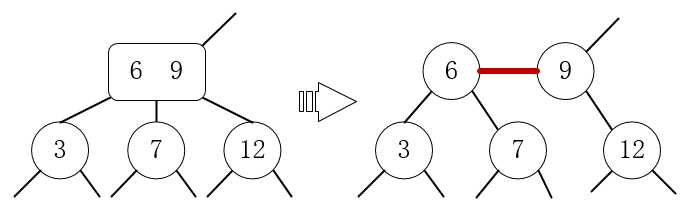
2.将所有的3-节点进行变换:
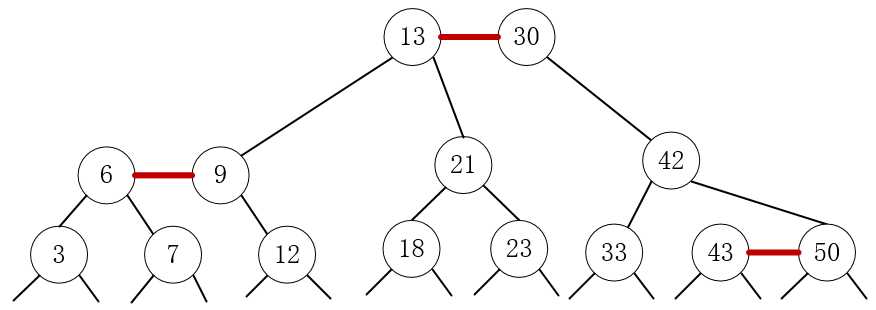
3.得到的就是一颗红黑树,所以2-3树和红黑树是可以一一对应的,但是需满足三个条件:
从图中可以看出,我们的红连接都是左链接,满足条件一。没有节点同时链接两条红线,满足条件二。每个叶子节点下得空链接到根节点30的路径中黑连接数量都是2,所以满足条件三。
三、红黑树
标签:img col 路径 str span 二叉树 直接 流程 auto
原文地址:https://www.cnblogs.com/leokale-zz/p/11123482.html