标签:span nbsp void cout space str fine 长度 col
下图表示城市之间的交通路网,线段上的数字表示费用,单向通行由A->E。试用动态规划的最优化原理求出A->E的最省费用。
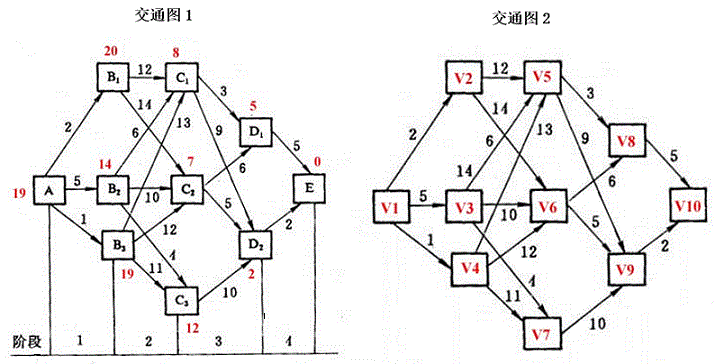
如图:求v1到v10的最短路径长度及最短路径。
第一行为城市的数量N;
后面是N*N的表示两个城市间费用组成的矩阵。
A->E的最省费用。
10 0 2 5 1 0 0 0 0 0 0 0 0 0 0 12 14 0 0 0 0 0 0 0 0 6 10 4 0 0 0 0 0 0 0 13 12 11 0 0 0 0 0 0 0 0 0 0 3 9 0 0 0 0 0 0 0 0 6 5 0 0 0 0 0 0 0 0 0 10 0 0 0 0 0 0 0 0 0 0 5 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0
minlong=19 1 3 5 8 10
#include<iostream> #include<stdio.h> using namespace std; #define N 1000+1 int a[N][N],n,dp[N][3]; int k[N],tot; void find(int k) { if(k!=1)find(dp[k][2]); cout<<k<<‘ ‘; } int main() { cin>>n; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) cin>>a[i][j]; for(int i=2;i<=n;i++)dp[i][1]=N; // for(int i=1;i<=n;i++)dp[i][2]=-1; k[1]=1;tot=1; for(int i=2;i<=n;i++) { for(int j=1;j<n;j++) { if(a[j][i]!=0) { if(dp[i][1]>a[j][i]+dp[j][1]) { dp[i][1]=a[j][i]+dp[j][1]; dp[i][2]=j; } } } } printf("minlong=%d\n",dp[n][1]); find(dp[n][2]); cout<<n<<endl; }
标签:span nbsp void cout space str fine 长度 col
原文地址:https://www.cnblogs.com/jzxnl/p/11142139.html