标签:信息 不能 list sample tps region base display ret
Samcompu拥有大量的"水"资源!!
Samcompu需要制定一个水计划。这个计划的主要目的就是为了避开老师监视的时间来水。
老师在中途会离开机房T次,第i次将会离开tim_i秒。Samcompu划水的时候可不是随便乱水的。他可是拥有"水"资源的。在他的库存中有N个可以水的网站。Samcompu拥有一种黑科技,他可以几乎不耗任何时间在网站与网站之间跳转并且把跳转的网页的信息秒存。也就是说,Samcompu并不需要在每一次跳转的时候花费时间去浏览网页。当然,这只局限于N个网站之间的N-1个跳转方式(保证每一个网站都可以跳转到另外的所有网站)。对于第i种跳转方式,第u_i个网站到第v_i个网站的跳转存在一个危险程度w_i,这个危险值可能会造成电脑卡死,如果Samcompu不能及时处理,那么就会完美地被老师发现。
值得一提的是,在被查水表很多次后,Samcompu总结出了一个规律:
老师走得越久,能够保证在被老师发现之前处理好电脑卡死的危险程度的上限就越高。简单来说,两者就是成正比的关系,比例系数为1。
可惜的是,Samcompu的黑科技并不稳定,在老师第i次离开的时候,第K_i个跳转方式就不可用了。
当然,每一次水都可以从任意一个网站开始,也可以从任意一个网站结束。
现在Samcompu想知道,对于第i次老师离开机房时,他能够有多少种不同的安全的水的方案。两种水的方案不同当且仅当这两种水的方案的第一个网站或者最后一个网站不同。
(补充说明: 一个安全的水的方案当且仅当当前是老师第j次离开教室时跳转的路径中不存在一个跳转方式i使得timj??wi?,每一次水完后不可用的跳转方式就会恢复。)
第一行两个正整数T, N
接下来N−1行,每一行三个正整数u_i, v_i?, w_i
接下来T行,每一行两个正整数m_i, K_i
T行,每行一个正整数表示有多少中安全的水的方案。
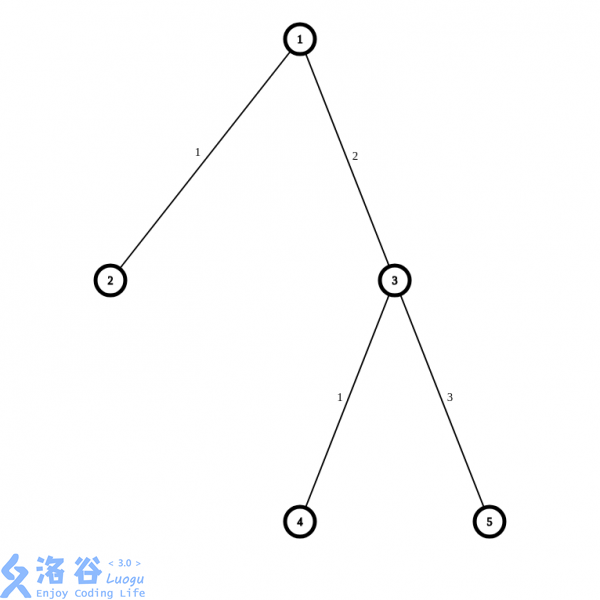
第一次连接1和2的边不可用,当前能经过的边的危险程度需要<1,并没有合法的方案。
第二次连接1和3的边不可用,当前能经过的边的危险程度需要<2,合法的方案有 (1,2) (2,1) (3,4) (4,3) 共四种。
第三次连接3和4的边不可用,当前能经过的边的危险程度需要<3,合法的方案有 (1,2) (1,3) (2,1) (2,3) (3,1) (3,2) 共六种。
提醒:本题计算答案按照点对的方式计算.也就是说,如果起点和终点一样,则只看做同一种方案.特别的,(x,y)(x,y)和(y,x)(y,x) (x≠y)算作两种不同的方案.
数据范围:
Subtask 1(30 pts):
1?Ki??N?10^3 1?timi?,wi??103
Subtask 2(50 pts):
1?T?5∗10^3 1?Ki??N?10^4 1?timi?,wi??10^3
Subtask 3(20 pts):
1?T?10^4 1?Ki??N?10^4 1?timi?,wi??10^3
数据保证不同的K_iKi?最多只有10^3个。
温馨提醒:由于出题人数据比较毒瘤,所以请尽量卡常。
分析:
我只想说出题人真的考虑了我的语文水平了吗。。。
事实上本题就是按并查集的方式加边,然后再在合并的时候进行计算。
至于失效直接保存即可。
CODE:
1 #include <cstdio> 2 #include <cstring> 3 #include <cmath> 4 #include <iostream> 5 #include <algorithm> 6 using namespace std; 7 const int M=100005; 8 int t,n,tot,ans[M],fa[M],now[M],sl[M],last; 9 int fr(){ 10 char c=getchar();int ans=0; 11 while (c<‘0‘||c>‘9‘) c=getchar(); 12 while (c>=‘0‘&&c<=‘9‘) ans=(ans<<1)+(ans<<3)+(c^48),c=getchar(); 13 return ans; 14 } 15 int found(int x){ 16 if (fa[x]==x) return x; 17 return fa[x]=found(fa[x]); 18 } 19 struct node{ 20 int tim,K,num; 21 }ask[M]; 22 struct node2{ 23 int from,to,adj,num; 24 }e[M]; 25 bool cmp(node x,node y){ 26 if (x.K==y.K) return x.tim<y.tim; 27 return x.K<y.K; 28 } 29 bool cmp2(node2 x,node2 y){ 30 return x.adj<y.adj; 31 } 32 void add(int u,int v,int w,int id){ 33 e[++tot].from=u;e[tot].to=v; 34 e[tot].adj=w;e[tot].num=id; 35 return; 36 } 37 int count(int x){ 38 return x*(x-1); 39 } 40 int main(){ 41 t=fr(),n=fr(); 42 for (int i=1;i<n;i++){ 43 int u=fr(),v=fr(),w=fr(); 44 add(u,v,w,i); 45 } 46 for (int i=1;i<=t;i++) ask[i].tim=fr(),ask[i].K=fr(),ask[i].num=i; 47 sort(ask+1,ask+1+t,cmp); 48 sort(e+1,e+n,cmp2); 49 for (int i=1;i<n;i++) now[e[i].num]=i; 50 for (int i=1;i<=t;i++){ 51 if (i==1||ask[i].K!=ask[i-1].K){ 52 for (register int j=1;j<=n;j++) fa[j]=j,sl[j]=1; 53 last=1;ans[ask[i].num]=0; 54 } 55 else ans[ask[i].num]=ans[ask[i-1].num]; 56 while (last<n&&e[last].adj<ask[i].tim){ 57 if (last!=now[ask[i].K]&&found(e[last].from)!=found(e[last].to)){ 58 int now1=found(e[last].from),now2=found(e[last].to); 59 ans[ask[i].num]+=count(sl[now1]+sl[now2])-count(sl[now1])-count(sl[now2]); 60 sl[now2]+=sl[now1];sl[now1]=0; 61 fa[now1]=now2; 62 } 63 last++; 64 } 65 } 66 for (int i=1;i<=t;i++) printf("%d\n",ans[i]); 67 return 0; 68 }
标签:信息 不能 list sample tps region base display ret
原文地址:https://www.cnblogs.com/kanchuang/p/11150457.html