标签:表示 层次遍历 放松 其它 分类 关联 指针 rds ima
首先了解三个概念
数据:所有能输入到计算机中并能够被计算机程序处理的符号的总称.它是计算机程序加工的原料
数据元素:数据的基本单位,在计算机程序中通常作为一个整体来进行考虑和处理.如数组中一个存储单元里面的数或者链表中一个结点
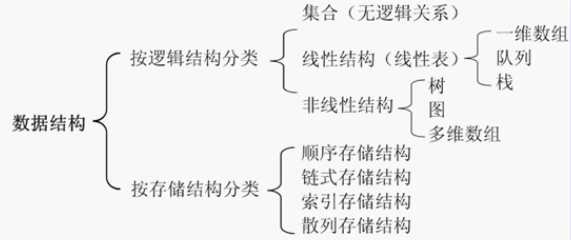
数据结构:是数据元素相互之间存在的一种或多种特定关系的集合.主要研究数据逻辑结构和存储结构及其运算的实现
数据的逻辑结构:结构定义中的“关系” 描述的是数据元素之间的逻辑关系,又称为逻辑结构,比如平常教学中所画的内存图,数组等为数据的逻辑结构.
数据的物理结构:数据结构在计算机中的实际表示形式称为数据的物理结构,又称为物理存储。
集合:结构中的数据元素之间除了“同属于一个集合”的关系外,别无其它关系。
线性结构:结构中的数据元素之间存在一个对一个的关系

树形结构:结构中的数据元素之间存在一个对多个的关系
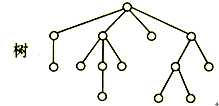
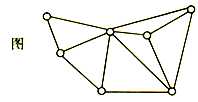
图:状结构或网状结构 结构中的数据元素之间存在多对多的关系

线性结构中又分为顺序表和链表(按物理存储结构划分),顺序表按顺序存储结构,链表按链式存储结构。
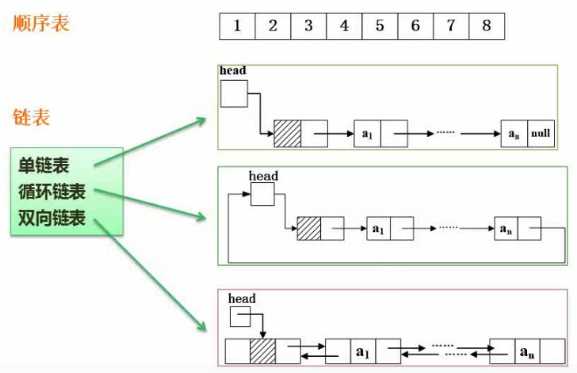
按顺序存储结构存储,内存中分配连续一段地址。
按链式存储结构。
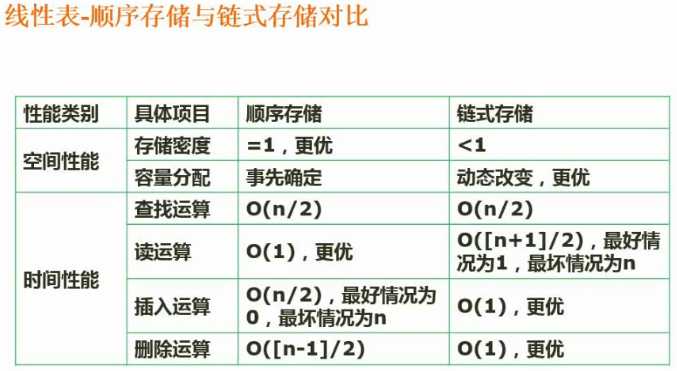

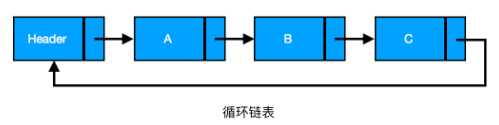

一维数组、队列、栈都是线性结构(逻辑)。
队列(FIFO)和栈(FILO)的物理存储结构实现方式既可以是顺序表也可以是链表。
一维数组的物理存储结构是顺序表。下标从0开始。
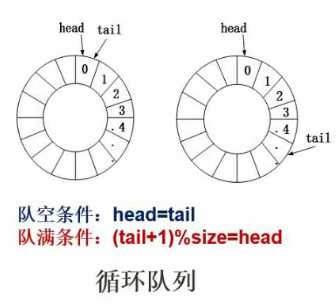
先进先出原则
头指针等于尾指针处于队空状态或队满状态。指针实际位置为指向队列下一个即将存储的区域。
先进后出原则
广义表(Lists,又称列表)是一种非线性的数据结构,是线性表的一种推广。即广义表中放松对表元素的原子限制,容许它们具有其自身结构。

结点的度:与下一层的几个节点相关联(下面有几个分支),结点的度就为几。
树的度:所有结点中度数最大的结点即为树的度(最大分支的结点)。
叶子结点:度为0的结点(下面没有分支)。
分支结点:除了叶子结点,其他都是分支结点,包括根结点(有分支的结点)。
内部结点:除了叶子结点和根结点,剩下的就是内部结点(除去根结点的分支结点)。
父结点、子结点、兄弟结点:相对的概念
层次:树从上到下的从1开始计算层次。
前序遍历:根在前面,然后子结点从左到右排序
中序遍历:根结点在中间
后序遍历:根在后面,然后子结点从左到右排序
层次遍历:从上到下(根结点开始),每层从左到右开始遍历
根据完全二叉树的特性,可以计算出任意节点n的双亲节点及左右孩子节点的序号,因此完全二叉树的节点可以按照从上到下从左到右的顺序依次存储到一维数组中。非完全二叉树存储时应先将其改造为完全二叉树,以空替代不存在的节点,比较浪费存储空间。
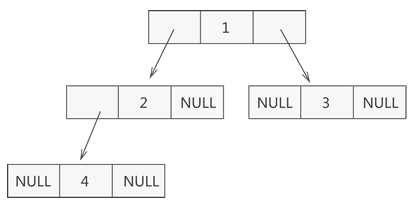
树结构链式存储类似线性结构链式存储,先定义包含数据域和引用域的节点(Node),然后通过引用域存储节点之间的关系。根据二叉树的结构来看,节点Node至少包含数据域(Data),引用域(左孩子LChild、右孩子RChild),为了方便通过孩子节点查找父节点,引用域中可以考虑添加父节点引用(Parent)。
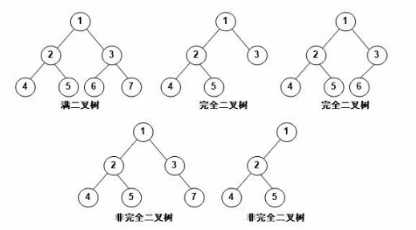
满二叉树:除了叶子结点,每个结点都有两个子结点
完全二叉树:只能缺叶子结点的右结点(从上到下从左到右的序号不能断)

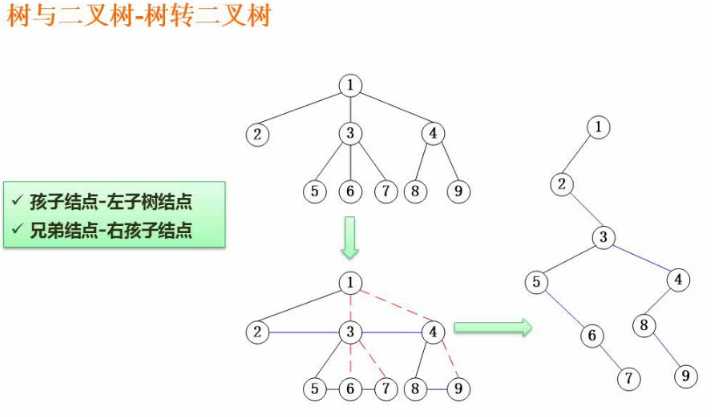
左孩子结点<根<右孩子节点
线性表中查找某个元素:从下标为0的元素开始遍历,如果使用排序二叉树,遍历的结点会少很多。

用于哈夫曼编码,节省存储空间和传输带宽,是无损压缩的方式。
树的路径长度:从根结点到某结点的边数 权: 存于叶子结点中代表某个字符出现的频度 带权路径长度:叶子结点的路径长度(从根结点到目的结点的路径长度)* 权值 树的带权路径长度(树的代价,尽量小):所有结点带权路径长度的总和
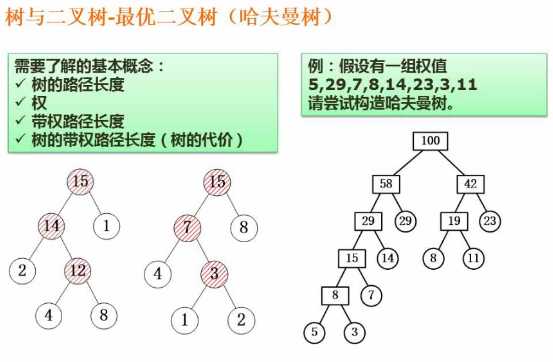
中间结点都是构造出来的,原始数据都是叶子结点。
右图中
树的路径为14
权是3,5,7,14,8,11,29,23这些叶子结点
7的带权路径为7*4=28,3的带权路径为3*5=15
树的带权路径为所有叶子结点的带权路径总和:3*5+5*5+7*4+14*3+。。。
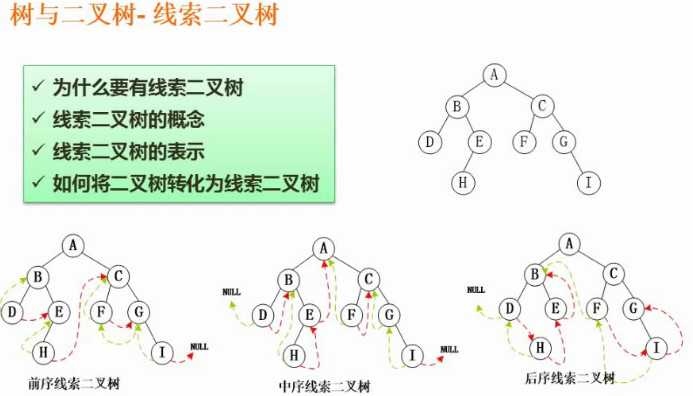
先把二叉树根据前序、中序、后序排序,然后根据序列就可以找到结点的前结点和后结点指向
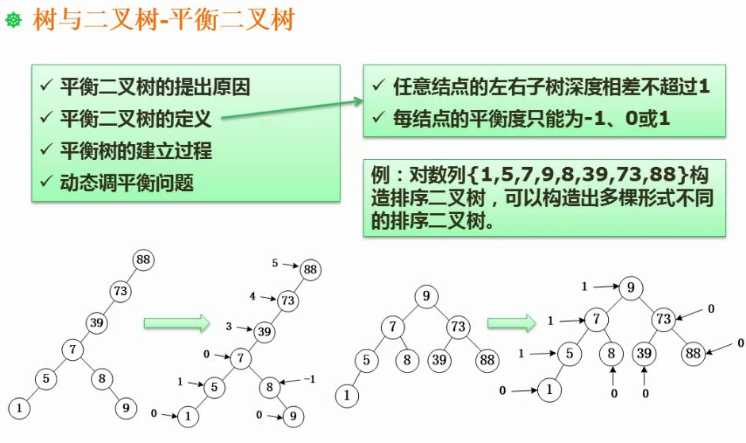
一棵平衡二叉树越平衡,查找效率越高。
定义
任意结点的左右子树深度相差不超过1 每个结点的平衡度只能为-1、0、1(结点平衡度 = 左子树深度-右子树深度)
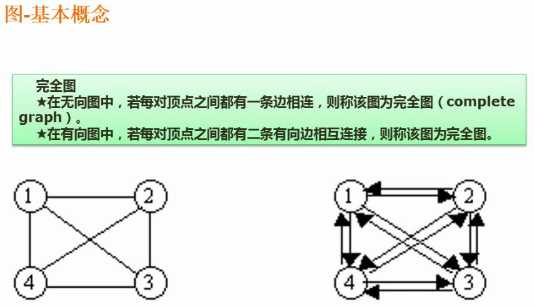
两个结点之间的连线不带箭头
两个结点之间的连线带箭头
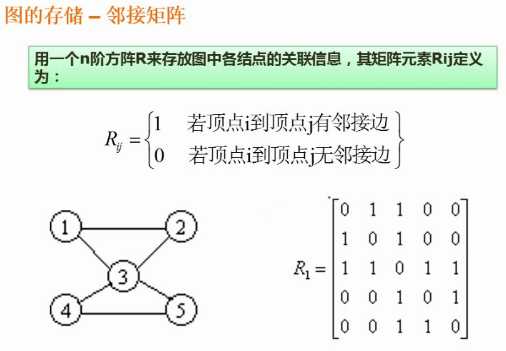
邻接矩阵为了节省存储空间可以只存上三角或者下三角(稀疏矩阵)
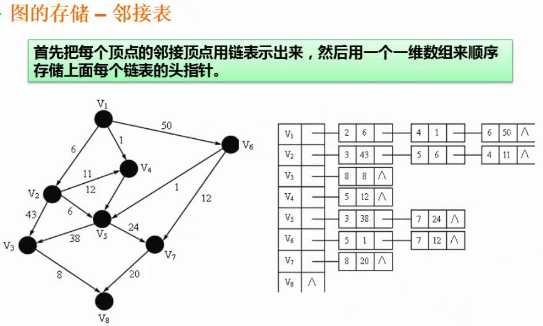
基于一维数组+链表
数组中存储所有的结点,数组存储的这个结点能到哪个相邻的结点用链表的方式连接起来。
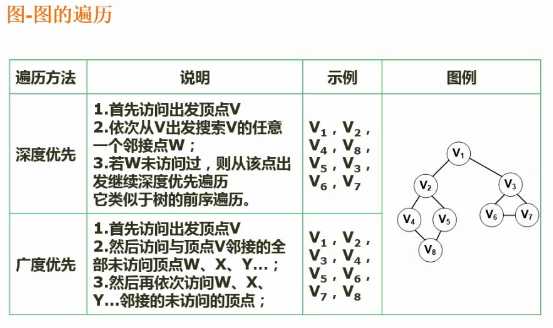
英文全称depthFirstSearch
V0 - V4 -》(V4链表)V6-》(V6链表)V7 -》(V7链表,V6已访问) 没有其他节点这条结束,回溯
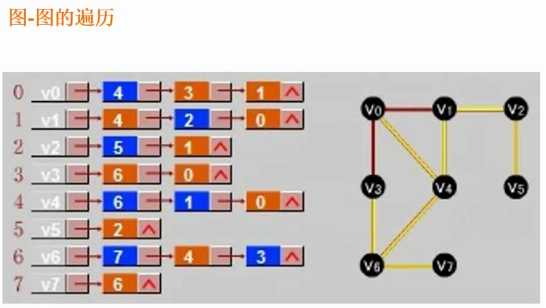
英文全称broadFirstSearch
V0 - V4 - V3 - V1 -》(V4链表,V1-V0已经访问过不再访问)V6-》(V3链表,V6-V0都已经访问过)-》(V1链表,V4-V0都已经访问) V2

完成某些任务需要先完成某些任务。用一个有向图表示
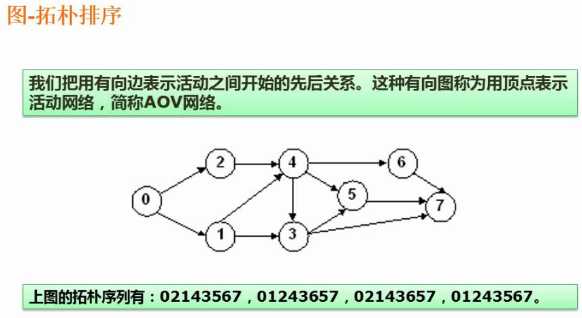
最小生成树,留下图中权值比较小的边。
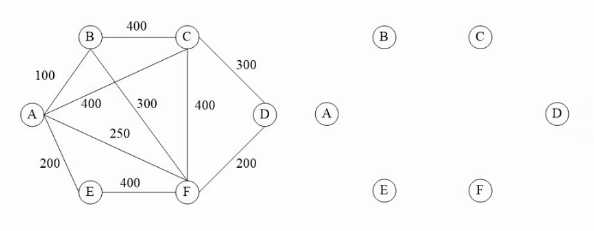
起点的所有边 - 》取最短的那条边连起来 -》两个点的所有边中最短边 -》连起来
直接找最短的边然后连起来。(边数 <= 结点数 - 1)
树是没有环路的(没有封闭区域)
树的结点为n,则边的最大值为n-1(即树:边数<=节点数-1)
二维数组的的变种稀疏矩阵,为了节省空间提出的概念,有上三角下三角之分。(邻接矩阵可以用这种方式存储)
标签:表示 层次遍历 放松 其它 分类 关联 指针 rds ima
原文地址:https://www.cnblogs.com/aeolian/p/10710817.html