HashMap的扩容机制

时间：2019-07-08 23:45:49 阅读：132 评论：0 收藏：0 [点我收藏+]

复习散列数据结构之余重新研究了一下Java中的HashMap；本文主要针对：1、HashMap的初始化；2、HashMap的插入；3：HashMap的扩容这三个方面进行总结

1、HashMap的初始化

首先我们来看看代码：

 1 public HashMap(int initialCapacity, float loadFactor) {
 2     if (initialCapacity < 0)
 3         throw new IllegalArgumentException("Illegal initial capacity: " +
 4                                            initialCapacity);
 5     if (initialCapacity > MAXIMUM_CAPACITY)
 6         initialCapacity = MAXIMUM_CAPACITY;
 7     if (loadFactor <= 0 || Float.isNaN(loadFactor))
 8         throw new IllegalArgumentException("Illegal load factor: " +
 9                                            loadFactor);
10     this.loadFactor = loadFactor;
11     this.threshold = tableSizeFor(initialCapacity);
12 }
13 
14 /**
15  * 返回一个等于指定容量的2的N次方的容量
16  * Returns a power of two size for the given target capacity.
17  */
18 static final int tableSizeFor(int cap) {
19     int n = cap - 1;
20     n |= n >>> 1;
21     n |= n >>> 2;
22     n |= n >>> 4;
23     n |= n >>> 8;
24     n |= n >>> 16;
25     return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
26 }

由此我们可知hashmap的容量总是2的N次方，而且这个值大于且最接近指定值大小的2次幂，比如就算我们指定new hashmap(1000),实际上构造出来的也是：hashmap(1024);

那问题来了：为什么JDK要这样做呢？

要解决这个问题我们需要看看hashmap的是如何找到元素的存放位置的：

方法一：
static final int hash(Object key) {   //jdk1.8 & jdk1.7
    int h;
    // h = key.hashCode() 为第一步 取hashCode值
    // h ^ (h >>> 16)  为第二步 高位参与运算
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
方法二：
static int indexFor(int h, int length) {  
//jdk1.7的源码，jdk1.8没有这个方法，取而代之的是在1.8中的putVal()方法中的第3行中：
//if ((p = tab[i = (n - 1) & hash]) == null))  
//原理都是一样的，作用也是一样的，都是定位元素位置
    return h & (length-1);  //第三步 取模运算
}，
看到这里我们自然会问：为什么hash()函数中要用对象的hashcode与自身的高16位进行异或运算（hashcode ^ (hashcode >>> 16)）？
这是一个很精妙的设计：
a:其实我们大可以直接用对象的hashcode直接作为下标来存储对象，这个值对于不同的对象必须保证唯一（JAVA规范），这也是大家常说的，重写equals必须重写hashcode的重要原因。但是对象的hashcode返回的是一个32位的int,那这个数组就有40亿左右，大部分情况下我们不需要这么长的数组，我们只需要低位就行，比如只根据低16位创建数组，那数组长度大概就只需要6万多，但是直接创建6万多长度的数组肯定也不合理，而且只取低16位的随机性肯定没有取32位的随机性大，冲突概率也更高，那JDK如何解决的呢？
b:JDK的处理非常巧妙，hashcode ^ (hashcode >>> 16) 该运算是用对象的hashcode与自己的高十六位进行异或运算，这样计算出来的hash值同时具有高位和低位的特性，这样算出来的hash值可以说就是一个增大了低十六位随机性的hashcoede。这样我们试想一下：只要对象的32位hashcode有一位发生了变化，那返回的hash值就会发生变化，更厉害的是不管这发生变化的那一位是高16位还是低16位，最后低十六位都会被影响到，这样也使得后面取模运算下标时所截取的低位的随机性增加，所计算出来的下标更加随机和均匀；
为什么JDK中要用h & (length-1)来计算元素存储位置下标？
计算元素的存放位置，我们首先想到的是根据对象的hash值对数组长度取模，这样元素的分布也还算均匀，但是取模运算效率不算高，所以JDK采用了h & (table.length -1)来得到该对象的保存位，数组长度是2的整次幂时，（数组长度-1）正好相当于一个“低位掩码”，“与”操作的结果就是散列值的高位全部归零，只保留低位值，用来做数组下标访问。以初始长度16为例，16-1=15。2进制表示是00000000 00000000 00001111。“与”操作的结果就是截取了最低的四位值。也就相当于取模操作，而且经过前面的hash()函数的的处理，低位的随机性增加了，所以可知最后运算得到的存储下标也会更加随机更加均匀。
综上：当length = 2^n时，不同的hash值发生碰撞的概率比较小，这样就会使得数据在table数组中分布较均匀，查询速度也较快。
2、HashMap的插入：
 public V put(K key, V value) {
       return putVal(hash(key), key, value, false, true);
   }

   final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
                  boolean evict) {
       Node<K, V>[] tab;
       Node<K, V> p;
       int n, i;
       // 如果表为空则创建，这也体现了hashmap是懒加载的，构造完hashmap之后，如果没有put操作，table是不会初始化的
       if ((tab = table) == null || (n = tab.length) == 0)
           n = (tab = resize()).length;
       // 这一步是根据hash值对数组长度取模，找到元素应该存放的位置，
       //JDk1.7中把该步骤写成另一个方法，1.8中直接写在此处
       //如果为空则创建一个节点
       if ((p = tab[i = (n - 1) & hash]) == null)
           tab[i] = newNode(hash, key, value, null);
       //不为空的情况
       else {
           Node<K, V> e;
           K k;
           // 节点已经存在，并且key一样，直接覆盖
           if (p.hash == hash &&
                   ((k = p.key) == key || (key != null && key.equals(k))))
               e = p;
           //判断是否是红黑树
           else if (p instanceof TreeNode)
               e = ((TreeNode<K, V>) p).putTreeVal(this, tab, hash, key, value);
           //执行到这里说明该位置存放的是链表
           else {
               for (int binCount = 0; ; ++binCount) {
                   if ((e = p.next) == null) {
                       p.next = newNode(hash, key, value, null);
                       //链表长度大于8转换为红黑树进行处理 TREEIFY_THRESHOLD = 8
                       if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                           treeifyBin(tab, hash);
                       break;
                   }
                   // key已经存在直接覆盖value
                   if (e.hash == hash &&
                           ((k = e.key) == key || (key != null && key.equals(k))))
                       break;
                   p = e;
               }
           }
           if (e != null) { // existing mapping for key
               V oldValue = e.value;
               if (!onlyIfAbsent || oldValue == null)
                   e.value = value;
               afterNodeAccess(e);
               return oldValue;
           }
       }
       ++modCount;
       // 超过最大容量threshold 就扩容
       if (++size > threshold)
           resize();
       afterNodeInsertion(evict);
       return null;
   }
3、HashMap的扩容：有了前面的铺垫，下面理解HashMap的扩容应该不会有太大的困难了：
我们先来看看JDK对扩容函数的注释：

/**
* Initializes or doubles table size.  If null, allocates in
* accord with initial capacity target held in field threshold.
* Otherwise, because we are using power-of-two expansion, the
* elements from each bin must either stay at same index, or move
* with a power of two offset in the new table.
*
* @return the table
*/
final Node<K,V>[] resize() {...}
这段话后面描述到：因为我们使用2的N次幂的扩容机制，所以元素在扩容后的数组中要么是留在原来的下标处，要么是在原位置基础上再移动2的N次幂
这有点费解，我们看一下下面的寻址过程：
 上图的（a）(b)分别对应扩容前和扩容后的hash&(n-1)也就是寻找元素存放位置的过程，可以看到扩容后的n-1相比扩容前的n-1多了一高位1，则再进行&运算时，key1和key2也多了一高位参与运算：
所以，原hash值新增参与运算的的那一bit如果是0，则在新数组中的下标不变，如果原hash值新增参与运算的那一bit是1，则在新数组中的下标为：原索引+原数组容量。
因此现在JDK只需要判断每个元素的hash值新增参与运算的那一bit是1还是0就可以给每个元素确定新数组中的位置，这样做可以巧妙的把原来处于同一个下标索引处的多个元素在新的数组中分散开来，如上面的（a）(b)过程，（a）过程中key1和key2虽然hash值不同，但是运算出了同一个索引值，所以存在同一个位置，但是在（b）过程中由于扩容的影响多了1bit参与运算，所以key1和key2就被分配到了不同的索引处！
下面看看JDK如何实现扩容，真是太巧妙了！

final Node<K,V>[] resize() {
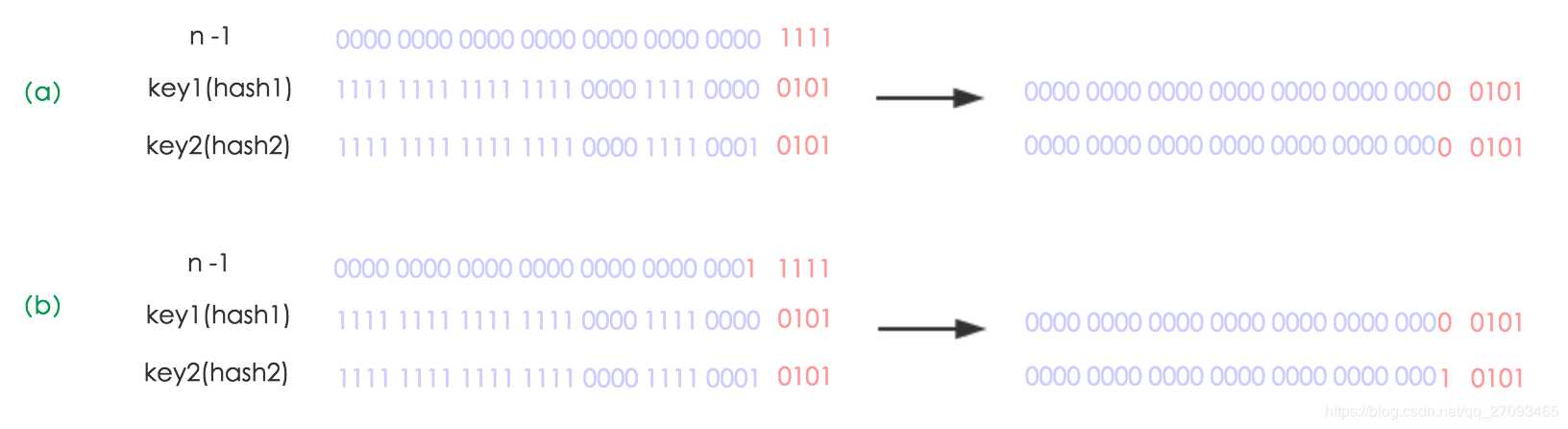
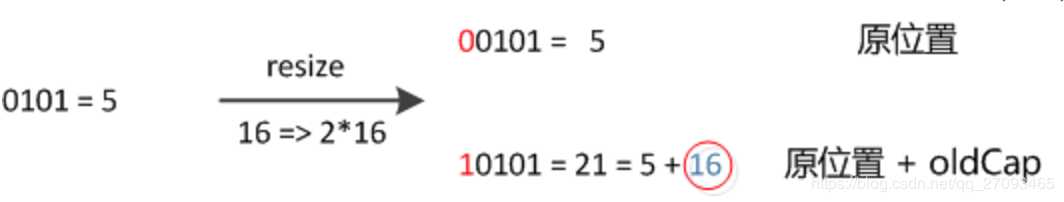
   Node<K,V>[] oldTab = table;
   int oldCap = (oldTab == null) ? 0 : oldTab.length;
   int oldThr = threshold;
   int newCap, newThr = 0;
   if (oldCap > 0) {
       if (oldCap >= MAXIMUM_CAPACITY) {
           threshold = Integer.MAX_VALUE;
           return oldTab;
       }
       else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
                oldCap >= DEFAULT_INITIAL_CAPACITY)
           newThr = oldThr << 1; // double threshold
   }
   else if (oldThr > 0) // initial capacity was placed in threshold
       newCap = oldThr;
   else {               // zero initial threshold signifies using defaults
       newCap = DEFAULT_INITIAL_CAPACITY;
       newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
   }
   if (newThr == 0) {
       float ft = (float)newCap * loadFactor;
       newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
                 (int)ft : Integer.MAX_VALUE);
   }
   threshold = newThr;
   @SuppressWarnings({"rawtypes","unchecked"})
       Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
   table = newTab;
   //移动数据
   if (oldTab != null) {
       for (int j = 0; j < oldCap; ++j) {
           Node<K,V> e;
           if ((e = oldTab[j]) != null) {
               oldTab[j] = null;
               if (e.next == null)
                   newTab[e.hash & (newCap - 1)] = e;
               else if (e instanceof TreeNode)
                   ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
               else { // preserve order
                   Node<K,V> loHead = null, loTail = null;
                   Node<K,V> hiHead = null, hiTail = null;
                   Node<K,V> next;
                   do {
                       next = e.next;
                       //把元素的hash值与旧的容量做&运算，便可得出元素的hash值
                       //新增的参与运算的那一bit是1还是0
                       //hash&(n-1) 与 hash & n  的区别：
                       //加入n为16，则n-1为：1111 ，n为：10000
                       //n比n-1高了一bit，且因为n为2的n次幂，
                       //所以，hash&n 可以得出扩容后元素hash值多参与运算的那一bit是0还是1
                       //新增参与运算的bit是0，则位置不变
                       if ((e.hash & oldCap) == 0) {
                           if (loTail == null)
                               loHead = e;
                           else
                               loTail.next = e;
                           loTail = e;
                       }
                       //新增参与运算的bit是1，位置变为： 原索引+原数组容量
                       else {
                           if (hiTail == null)
                               hiHead = e;
                           else
                               hiTail.next = e;
                           hiTail = e;
                       }
                   } while ((e = next) != null);
                   if (loTail != null) {
                       loTail.next = null;
                       //位置不变
                       newTab[j] = loHead;
                   }
                   if (hiTail != null) {
                       hiTail.next = null;
                       //位置变为： 原索引+原数组容量
                       newTab[j + oldCap] = hiHead;
                   }
               }
           }
       }
   }
   return newTab;
}
 第一次写博客，有很多表述可能不是很清楚，望谅解。

HashMap的扩容机制

标签：pes http 的区别 ESS sam 运算移动 because 随机

原文地址：https://www.cnblogs.com/mochenghui/p/11154547.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行