标签:今天 正整数 运行时间 作者 枚举 成绩 trie 字母 后缀数组
估分:100+30+30
实际:100+27+63
Rank 11
今天的题是一整套欺诈题
全都可以暴力跑过
xzb选拔赛
wyl8899今天也很刻苦的在做老师布置下来的题目!
这一天老师布置的题目是这样的:
给出两个仅含小写字母的字符串A和B,输出最大的k,使得A[1..k]是B的子串。
A和B的长度都不会超过50000。
很显然他并不知道正确的做法,但是他居然卡着时间过掉了老师给的数据!
你找到了他提交给老师的程序,经过测试你惊讶的发现,他的程序运行时间恰好是最终答案,单位是毫秒。
你现在找到了老师给的数据中的一笔,你决定至多修改A串中的一个字母,使得他的程序尽可能的慢。
现在,你能告诉我修改数据之后他的程序在这个测试点的运行时间么?(单位当然还是毫秒)
保证A和B的长度都不超过50000。
首先二分答案,只保留A串的前面mid个,然后分别从前往后,从后往前做一遍KMP,求出B串中每个点往左往右最长匹配多少A串的字符,记为ma1[i]与ma2[i]
然后枚举换哪B串哪一个字符,设x是ma1[i-1]跳若干次next1数组得到的值,y是ma2[i+2]跳若干次next2数组得到的值,若x+2=ma2[i+1]或ma1[i-1]+2=y就可行
虽然这样做很假,但是跟暴力拍了10分钟都没有错,我猜它应该是对的吧
方法一:先枚举更改位置,然后二分
方法二:把B和A接在一起跑后缀数组
都不会
树上的最长不下降子序列
n<=100000,每个数的权值都是1到n的正整数。
暴力27分
在序列上求最长不下降子序列的一种做法是建一颗权值线段树,维护f的最大值,每次就是询问权值在 1-wi 中 f
值的最大值。
既然是在树上,那每次求一个节点的答案时就把它的儿子的权值线段树合并一下就好了
时间复杂度O(\(n logn\))
在序列上求最长不下降子序列的另一种做法是维护一个单调队列。对于节点 i,单调队列中可能的点,只会是其所有儿子对应的单调队列中的元素再加上自己。所以我们要做的,只是将这个点的儿子们的单调队列们进行合并,再加入自己。
利用启发式合并可以做到O(\(nlog^2n\))
这种方法又好打又快
若一个点x可以转到y,需要满足的条件是:
这是一个二维偏序问题嘛,按v排序后把每个x的f插入权值线段树中dfn的位置,查询时区间查询就可以了
甚至你可以打CDQ分治,不过很慢,多一个log就是了
时间复杂度O(\(nlogn\))
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
struct qy
{
int v,dfn,size,x,f;
};
int n,i,j,x,y,ll,rr,mid,ma,tott;
int fa[100005];
int son[100005],next[100005],last[100005],tot;
int ans[100005],g[100005];
qy a[100005];
int tree[400005];
void insert(int x,int y)
{
tot++;
son[tot]=y;
next[tot]=last[x];
last[x]=tot;
}
void dg(int x)
{
a[x].dfn=++tott;
a[x].size=1;
for (int i=last[x];i>=1;i=next[i])
{
dg(son[i]);
a[x].size+=a[son[i]].size;
}
}
int comp(qy a,qy b)
{
return ((a.v>b.v)||((a.v==b.v)&&(a.dfn<b.dfn)));
}
int compp(qy a,qy b)
{
return a.x<b.x;
}
int query(int k,int l,int r,int x,int y)
{
if ((l<=y)&&(r>=x))
{
if ((l>=x)&&(r<=y))
{
return tree[k];
}
int mid=(l+r)/2;
return max(query(k*2,l,mid,x,y),query(k*2+1,mid+1,r,x,y));
}
else
return 0;
}
void modify(int k,int l,int r,int x,int y)
{
if (l==r)
{
tree[k]=y;
}
else
{
int mid=(l+r)/2;
if (x<=mid) modify(k*2,l,mid,x,y);
else modify(k*2+1,mid+1,r,x,y);
tree[k]=max(tree[k*2],tree[k*2+1]);
}
}
int main()
{
freopen("read.in","r",stdin);
scanf("%d",&n);
for (i=1;i<=n;i++)
{
scanf("%d",&x);
fa[i]=x;
if (x!=-1)
insert(x,i);
}
for (i=1;i<=n;i++)
scanf("%d",&a[i].v),a[i].x=i;
dg(1);
sort(a+1,a+1+n,comp);
for (i=n;i>=1;i--)
{
a[i].f=query(1,1,n,a[i].dfn,a[i].dfn+a[i].size-1)+1;
modify(1,1,n,a[i].dfn,a[i].f);
}
sort(a+1,a+1+n,compp);
for (i=1;i<=n;i++)
{
printf("%d ",a[i].f);
}
}是道吼题啊
法法塔和wyl8899都喜欢玩游戏。但是每次玩游戏法法塔都被wyl8899虐。
为了安慰可怜的法法塔,wyl8899决定大发慈悲,修改了一下游戏规则。
是这样的,这儿有一堆石子排成一列,每次wyl8899让hza选择一个区间进行游戏。游戏嘛,就是采用最普通的规则:两人轮流操作,每次选择一堆石子,取掉不为0的石子数,没法操作者失败。法法塔要做的是这样的:
我们现在定义一个区间的弱菜值:表示如果法法塔先取石子,而且法法塔第一步取的石子规定是最右边的那堆的话,为了必胜,第一步需要取的石子数。如果没法获胜的话,那么弱菜值就是-1。
法法塔要选择一个区间[l,r],使得r为wyl8899给定的某个数,l属于[a,b],a,b也是wyl8899给定的,要求这个区间的弱菜值是满足前面的条件中最大。请给出这个最大的弱菜值。
如果最大弱菜值不为-1,法法塔就会马上取走该区间最右端的石子堆最大弱菜值数量的石子。
n<=100000,m<=10000,每堆的石子数<=1000。
一看数据范围我就知道这题放暴力过——lyl
暴力。
加几个小优化再吸一口臭氧就切了
我们将数列分成 √n 块。每个块内维护个 trie。这样查询操作只需要访问每个块,若查询的区间包含了整个块,那么就直接在 trie 内查询,否则暴力扫描整个块(这样的块不会超过两个)。修改操作,暴力扫描要修改的块。若整个块都要被修改,那么直接打上个修改标记 delta,表示将该区间内的所有数异或上 delta,由于异或满足很多很多性质,所以只需要将询问的数异或上 delta 就行了。否则暴力修改区间内的所有数,然后重新建立 trie(这样的块也不会超过两个)。于是我们得到了 O(n√nlogS) 的算法,其中 S 为数的大小,这儿不会超过10。经实际检验,比暴力稍稍快一点。这就是正解了。当然啦,我相信经过优化的暴力一定也能过的 。
应该没什么人会想打正解吧…
同学们上濠头中学的愿望破灭了
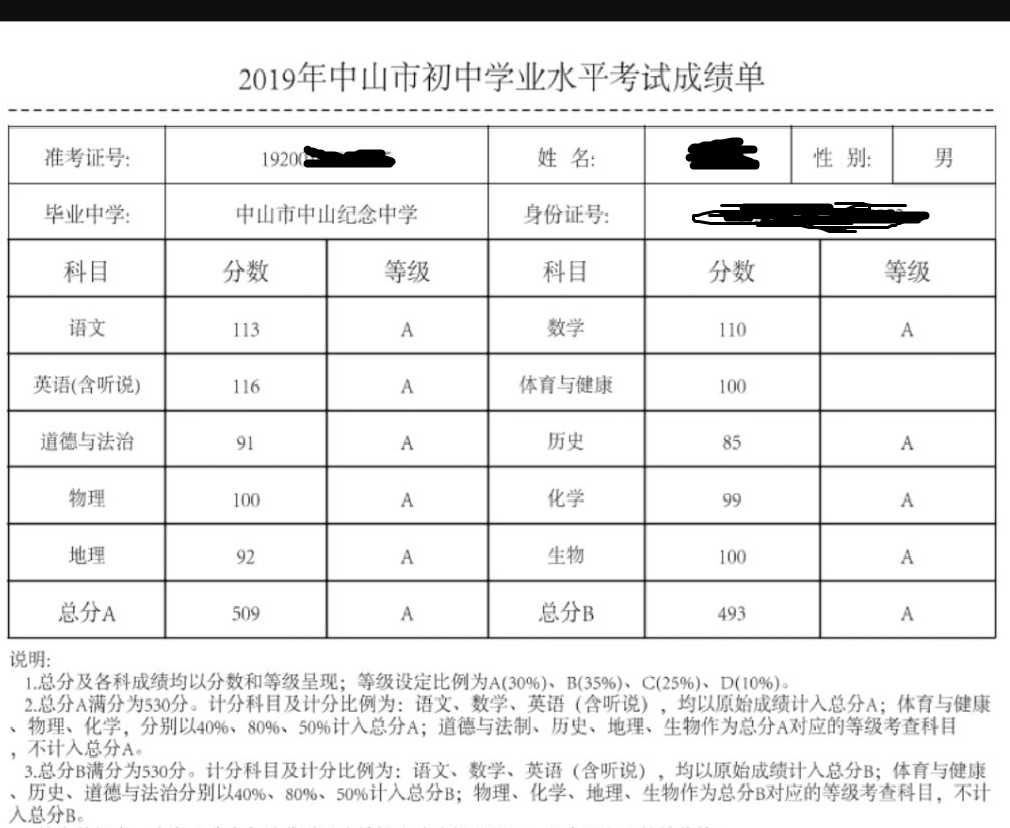
我觉得海星
差一分屏蔽海星
Dramatic…
cgh也是509分,差体育的一分
当年有一个你们的学长啊,中考体育39分,就差这一分屏蔽啦,所以你们一定要重视体育啊,中考前不要打篮球呀!
这个故事体育老师们应该可以说十年
恭喜dyp,zys,597三位大爷屏蔽
标签:今天 正整数 运行时间 作者 枚举 成绩 trie 字母 后缀数组
原文地址:https://www.cnblogs.com/leason-lyx/p/11159344.html