标签：交互 相对 min cell padding 假设 out str 功能实现
将内层位移换算到外层
在3维场景功能实现中，需要制作有类似于UG中使用坐标系来转动和平移节点的功能，在实现过程发现，
如果将平移层置于旋转功能层内，则：旋转时，如果事先经过了平移操作，将导致节点在场景中甩动，而不在移动中心转动；
如果将平移动层置于旋转功能层外，则：平移时，如果事先经过了旋转，将导致节点在场景中非坐标轴方向平移，而不是按原传感器方向平移。
思考之后，方案如下：在旋转层内外各旋转一个平移层，在每次内层平移（保证按坐标轴平移）完成之后，将内层的平移数据，换算到外层，再将内层数据复位到平移开始时的状态，以保证内层节点位置相对世界坐标系不变，且不影响旋转（不至产生甩动现象）和下次平移。
具体做法分两种，其一，在场景内部以脚本方式转换，不需要组件参与；其二，在场景中将传感器取得的值路由给组件，然后利用引擎内置算法处理，再将值设置到场景中，涉及到较多交互。
若采用做法一，则以下是相关算法。
一、旋转算法
这个问题比较简单，网上已经有较多总结：
设旋转前坐标为
，旋转后坐标为
。
公式表示：
x′=cosγ⋅x−sinγ⋅y
y′=sinγ⋅x+coγ⋅y
z′=z
最后是代码表示
|
|
公式表示：
x′=cosβ⋅x+sinβ⋅z
y′=y
z′=−sinβ⋅x+cosβ⋅
最后是代码表示
|
|
公式表示：
x′=x
y′=cosα⋅y−sinα⋅z
z′=sinα⋅y+sinα⋅z
最后是代码表示
|
|
首先，需要定义"任意轴"的单位向量，例如X轴可以用向量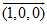
来表示。
那么假设旋转轴的单位向量为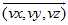
，旋转前坐标为
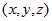，旋转后坐标为
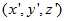，旋转角为
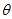，于是有：
x′=(vx⋅vx⋅(1−cosθ)+cosθ)⋅x+(vx⋅vy⋅(1−cosθ)−vz⋅sinθ)⋅y+(vx⋅vz⋅(1−cosθ)+vy⋅sinθ)⋅z
y′=(vx⋅vy⋅(1−cosθ)+vz⋅sinθ)⋅x+(vy⋅vy⋅(1−cosθ)+cosθ)⋅y+(vy⋅vz⋅(1−cosθ)−vx⋅sinθ)⋅z
z′=(vx⋅vz⋅(1−cosθ)−vy⋅sinθ)⋅x+(vy⋅vz⋅(1−cosθ)+vx⋅sinθ)⋅y+(vz⋅vz⋅(1−cosθ)+cosθ)⋅z
计算时照着公式代入即可。
最后给出代码实现：
|
|
标签：交互 相对 min cell padding 假设 out str 功能实现
原文地址：https://www.cnblogs.com/ice-arrow/p/11164691.html
