标签:vol 相对 ati href poi 缓存 依赖 nal tran
(翻译,图片也来自原文)
绝大部分计算机的显示器是二维的(a 2D surface)。在OpenGL中一个3D场景需要被投影到屏幕上成为一个2D图像(image)。这称为投影变换(参见这或这),需要用到投影矩阵(projection matrix)。
首先,投影矩阵会把所有顶点坐标从eye coordinates(观察空间,eye space或view space)变换到裁剪坐标(clip coordinated,属于裁剪空间,clip space)。然后,这些裁剪坐标被变换到标准化设备坐标(normalized device coordinates, NDC,即坐标范围在-1到1之间),这一步是通过用用裁剪坐标的\(w_c\)分量除裁剪坐标实现的。
因此,我们要记住投影矩阵干了两件事: 裁剪clipping(即frustum culling,视景体剔除)和生成NDC。下文会讲述如何根据6个参数(left, right, bottom, top, near和far边界值)来构建投影矩阵。
注意视景体剔出(也即clipping)是在裁剪坐标下完成的,是早于用\(w_c\)(即上面提到的\(w\)分量,c表示clipping)除裁剪坐标的(它会生成NDC)。裁剪坐标\(x_c, y_c, z_c\)会与\(w_c\)进行比较。如果裁剪坐标比\(-w_c\)小或者比\(w_c\)大,则丢弃这个顶点(vertex)。即经裁剪后剩余的顶点的裁剪坐标满足:\(-w_c < x_c, y_c, z_c < w_c\)。OpenGL会成发生裁剪的地方生成新的边,如下图1,一个三角形经裁后,成了一个梯形,两条红色的边就是裁剪后新生成的。
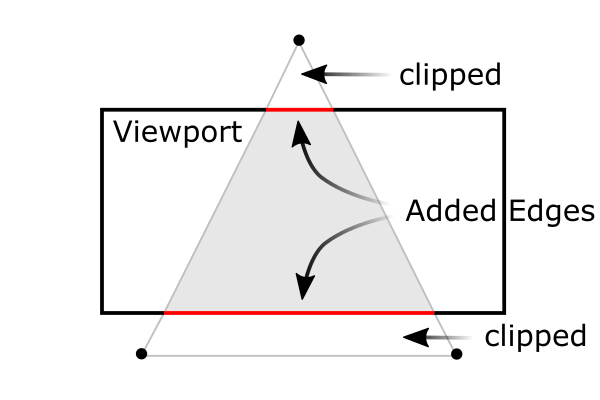
(图1. 一个被视体裁剪的三角形)
一般常用的有透视投影和正交投影,相应地也就有两种投影矩阵。
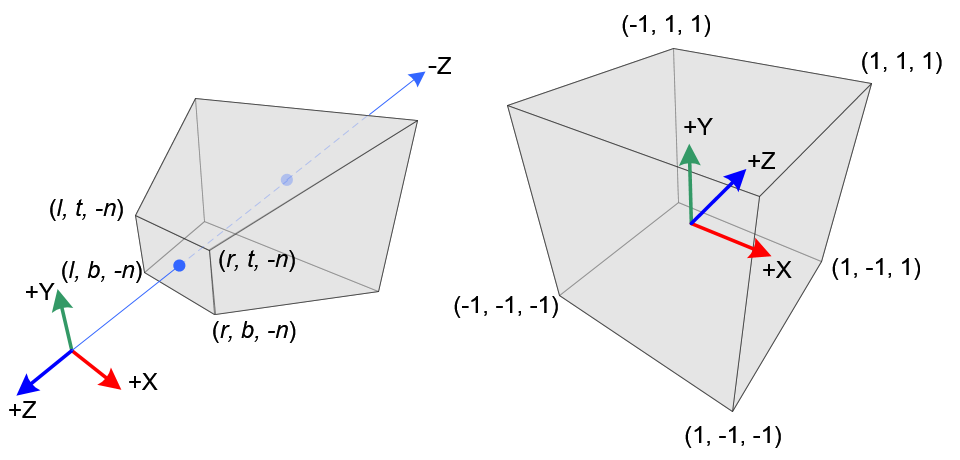
(图2. 透视投影中的视景体和标准化设备坐标NDC)
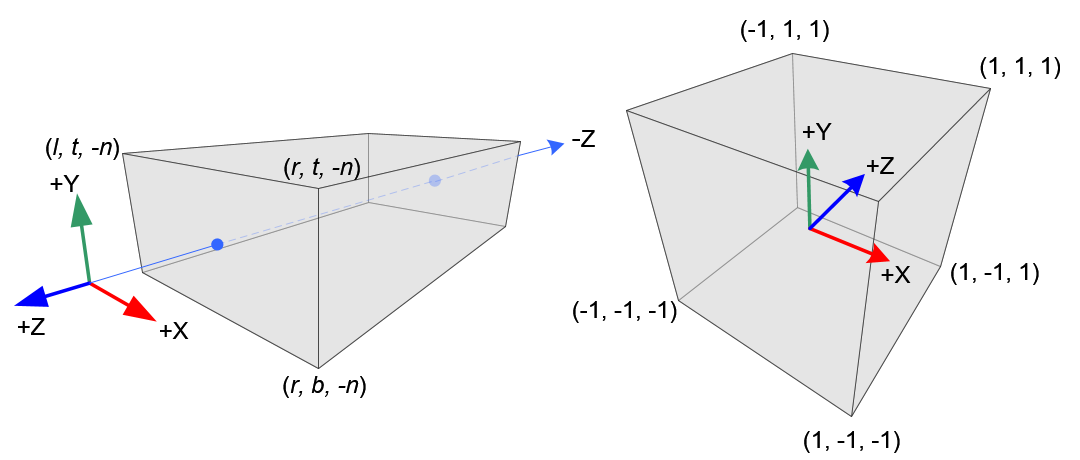
在透视投影中,一个3D point是在一个截头锥体中(truncated pyramid frustum,上面图2左图,即一个棱台),会被映射到一个立方体(NDC坐标空间)中,x坐标范围从[1, r]变成了[-1, 1],y坐标范围从[b, t]变成了[-1, 1],z坐标从[-n, -f]变成了[-1, 1]。
注意在view space中(即eye coordinate),OpenGL使用的是右手坐标系(上面图2左图),但是在NDC中使用的是左手坐标系(上面图2右图)。这样的话,在view space中camera位于坐标原点看向-z轴,而在NDC中camera是看向+z轴的。上面图2中的n表示近裁剪面(near plane),是正值。因为glFrustum()接受的near、far的值是正的,所以在在构造投影矩阵时,要为它们取负(negate them)。
在OpenGL中,view space(又称为eye space)中的一个3D point被投影到近裁剪面(此处用近裁剪面作投影平面,projection plane)上。下图3和图4显示了eye space中的一个点\((x_e, y_e, z_e)\)是怎样被投影成近裁剪面上的一个点\((x_p, y_p, z_p)\)。
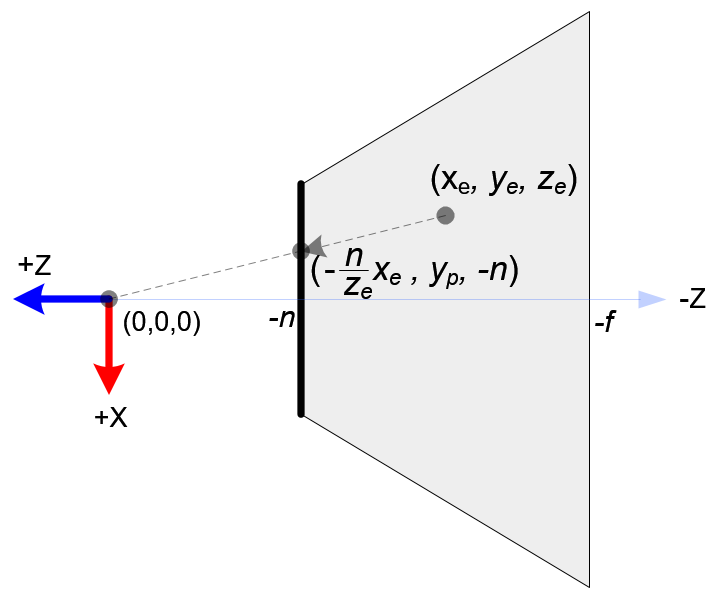
(图3. 视景体的俯视图)
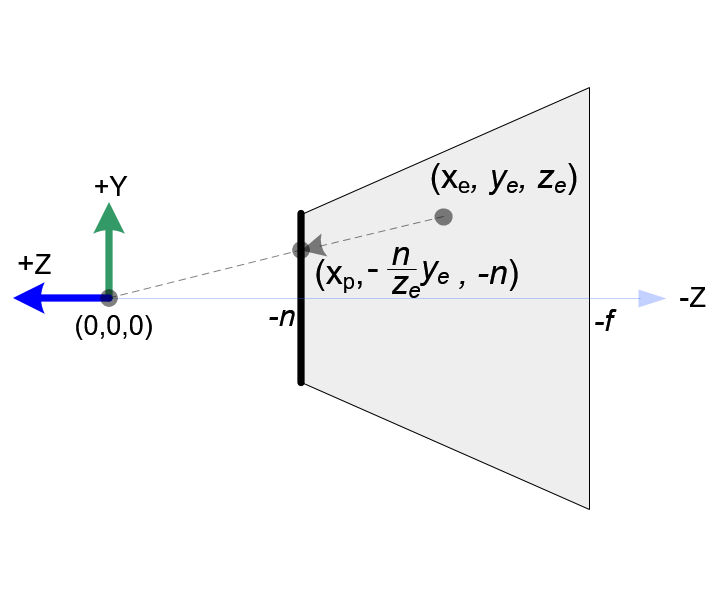
(图4.视景体的侧视图)
从视景体的俯视图(图3)看,x轴坐标\(x_e\)被映射成为\(x_p\),而\(x_p\)可以根据三角形相似形计算出来:
\[ \frac{x_p}{x_e}=\frac{-n}{z_e} \Longrightarrow x_p = \frac{-n\cdot x_e}{z_e}=\frac{n\cdot x_e}{-z_e} \]
从视景体的侧视图(图4)看,可以用相似的方法计算出\(y_p\):
\[ \frac{y_p}{y_e}=\frac{-n}{z_e} \Longrightarrow y_p = \frac{-n\cdot y_e}{z_e}=\frac{n\cdot y_e}{-z_e} \]
注意\(x_p\)和\(y_p\)都依赖\(z_e\)并与\(-z_e\)成反比。这是构建投影矩阵的第一个线索。在eye coordinates被投影矩阵乘后,得到的裁剪坐标仍然是齐次坐标(homogeneous coordinates)。最终它需要除以裁剪坐标的w分量,才能变成标准化设备坐标(NDC)。
\[ \left( \begin{matrix} x_{clip}\y_{clip}\z_{clip}\w_{clip} \end{matrix} \right) = M_{projection}\cdot \left( \begin{matrix} x_{eye}\y_{eye}\z_{eye}\w_{eye} \end{matrix} \right), \left( \begin{matrix} x_{ndc}\y_{ndc}\z_{ndc} \end{matrix} \right)=\left( \begin{matrix} \frac{x_{clip}}{w_{clip}}\\frac{y_{clip}}{w_{clip}}\\frac{z_{clip}}{w_{clip}} \end{matrix} \right) \]
因此,我们可以把裁剪坐标的w分量设置为\(-z_e\),则投影矩阵第4行变为(0, 0, -1, 0)。
\[ \left( \begin{matrix} x_c\y_c\z_c\w_c \end{matrix} \right)=\left( \begin{matrix} \cdot & \cdot &\cdot &\cdot\\cdot & \cdot &\cdot &\cdot\\cdot & \cdot &\cdot &\cdot\0 & 0 & -1 & 0 \end{matrix} \right) \left( \begin{matrix} x_e\y_e\z_e\w_e \end{matrix} \right), \therefore w_c=-z_e \]
接下来,我们把刚计算得到的\(x_p, y_p\)线性地(with linear relationship)映射到NDC中的\(x_n, y_n\)(这里的n表示NDC):\([l, r] \Rightarrow [-1, 1]\),\([b, t] \Rightarrow [-1, 1]\)。
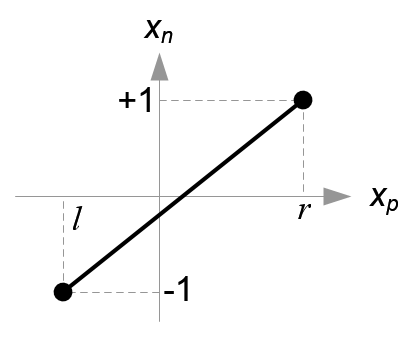
(图5. 把\(x_p\)映射到\(x_n\))
因为\(x_p\)和\(x_n\)之间是线性映射关系,如图5,所以可设两者之间的映射函数为:
\[
x_n = \frac{1-(-1)}{r-l}\cdot + \beta
\]
把\((x_p, x_n) = (r, l)\)代入上面方程得:
\[
1 = \frac{2r}{r-l}+\beta
\]
所以
\[
\begin{equation}
\begin{aligned}
\beta&=1 - \frac{2r}{r-l}=\frac{r-l}{r-l} - \frac{2r}{r-l}\&=\frac{r-l-2r}{r-l}=\frac{-r-l}{r-l}=-\frac{r+l}{r-l}
\end{aligned}
\end{equation}
\\therefore x_n=\frac{2x_p}{r-l}-\frac{r+l}{r-l}
\]
同理,可以求出\(y_p\)和\(y_n\)之间的关系表达式,如图6及以下公式:
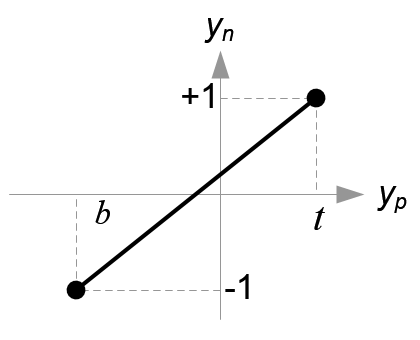
(图6.把\(y_p\)映射到\(y_n\))
\[
y_n = \frac{1-(-1)}{t-b}\cdot y_p + \beta
\]
用$ (y_p, y_n)=(t,1)$代入上式得
$$
1 = \frac{2t}{t-b}+\beta\
\begin{equation}
\begin{aligned}
\beta &= 1 - \frac{2t}{t-b} = \frac{t-b}{t-b} - \frac{2t}{t-b}\
&=\frac{t-b-2t}{t-b}=\frac{-t-b}{t-b}=-\frac{t+b}{t-b}
\end{aligned}
\end{equation}
\
\therefore y_n=\frac{2y_p}{t-b}-\frac{t+b}{t-b}
$$
接下来,把上上面求得的\(x_p=\frac{nx_e}{-z_e}\)和\(y_p=\frac{ny_e}{-z_e}\)代入刚刚求到的线性关系式得:
\[ \begin{equation} \begin{aligned} x_n &= \frac{2x_p}{r-l}-\frac{r+l}{r-l}\&= \frac{2\cdot \frac{n\cdot x_e}{-z_e}}{r-l}-\frac{r+l}{r-l}\&= \frac{2n\cdot x_e}{(r-l)(-z_e)} - \frac{r+l}{r-l}\&= \frac{\frac{2n}{r-l}\cdot x_e}{-z_e} - \frac{r+l}{r-l}\&= \frac{\frac{2n}{r-l}\cdot x_e}{-z_e} + \frac{\frac{r+l}{r-l}\cdot z_e}{-z_e}\&= \left. \left(\underbrace{\frac{2n}{r-l}\cdot x_e + \frac{r+l}{r-l}\cdot z_e}_{x_c}\right) \middle/ (-z_e) \right. \end{aligned} \end{equation} \]
\[ \begin{equation} \begin{aligned} y_n &= \frac{2y_p}{t-b} - \frac{t+b}{t-b}\&= \frac{2\cdot \frac{n\cdot y_e}{-z_e}}{t-b} - \frac{t+b}{t-b}\&= \frac{2n\cdot y_e}{(t-b)(-z_e)} - \frac{t+b}{t-b}\&= \frac{\frac{2n}{t-b}\cdot y_e}{-z_e} - \frac{t+b}{t-b}\&= \frac{\frac{2n}{t-b}\cdot y_e}{-z_e} + \frac{\frac{t+b}{t-b}\cdot z_e}{-z_e}\&= \left. \left(\underbrace{\frac{2n}{t-b}\cdot y_e + \frac{t+b}{t-b}\cdot z_e}_{y_c}\right) \middle/ (-z_e) \right. \end{aligned} \end{equation} \]
注意上面刚刚求得的\(x_n, y_n\)是NDC坐标,而NDC应该是由裁剪坐标除以\(w_c\)得到,也即透视除法(perspective division), \((x_c/w_c, y_c/w_c)\)。又因为,之前我们把\(w_c\)的值设置为\(-z_e\),所以上面\(x_n, y_n\)表达式中括号里的部分表示裁剪空间的坐标\(x_c, y_c\)。
加上上面的两个方程,我们可以找到投影矩阵的第1行和第2行:
\[ \begin{equation} \left( \begin{matrix} x_c\y_c\z_c\w_c \end{matrix} \right) =\left( \begin{matrix} \frac{2n}{r-l} & 0 & \frac{r+l}{r-l} & 0\0 & \frac{2n}{t-b} & \frac{t+b}{t-b} & 0\\cdot & \cdot & \cdot & \cdot\0 & 0 & -1 & 0 \end{matrix} \right) \left( \begin{matrix} x_e\y_e\z_e\w_e \end{matrix} \right) \end{equation} \]
现在矩阵只剩下第三行是待求解的。在eye space中\(z_e\)总是被投影到近裁剪面(near plane)上,即值总是为-n。但是我们为了完成裁剪(clipping)和深度测试(depth test),每一个顶点应该具有不同的z值。此外,投影变换应该是可逆的。既然我们知道z不依赖于x和y的值,那么我们就借用w分量来找到\(z_n\)和\(z_e\)之间的关系。因此,我们可以指定第三行长这样:
\[ \begin{equation} \left( \begin{matrix} x_c\y_c\z_c\w_c \end{matrix} \right) =\left( \begin{matrix} \frac{2n}{r-l} & 0 & \frac{r+l}{r-l} & 0\0 & \frac{2n}{t-b} & \frac{t+b}{t-b} & 0\0 & 0 & A & B\0 & 0 & -1 & 0 \end{matrix} \right) \left( \begin{matrix} x_e\y_e\z_e\w_e \end{matrix} \right) \end{equation}, z_n=z_c/w_c=\frac{Az_e + Bw_e}{-z_e} \]
因为在eye space中,\(w_e\)总是等于1,因此:
\[
z_n = \frac{Az_e + B}{-z_e}
\]
(注意,\(w_c = -z_e, w_e=1\)别搞混淆了)
为了找到系数A和B,我们把\((z_e, z_n)\)之间的关系: (-n, -1)和(-f, 1),代入上面这个等式中,得到:
\[ \begin{equation} \left\{ \begin{array}{lr} \frac{-An+B}{n} = -1 & \\frac{-Af+B}{f} = 1 & \end{array} \right. \end{equation} \\Downarrow \]
\[ \begin{equation} \left\{ \begin{array}{lr} -An + B = -n & (1)\-Af + B = f & (2) \end{array} \right. \end{equation} \]
由方程(1)可得:
\[
\begin{equation}
\begin{array}{lr}
B=An-n & (1')
\end{array}
\end{equation}
\]
把方程(1‘)代入到方程(2),可解出A:
\[
\begin{equation}
\begin{array}{lr}
-Af + (An-n) = f & (2')\-(f-n)A=f+n &\A=-\frac{f+n}{f-n}&
\end{array}
\end{equation}
\]
把A的值代入方程(1‘)可求得B:
\[
\begin{equation}
\begin{aligned}
B &=-n - \left(\frac{f+n}{f-n}\right)n=-\left(1+\frac{f+n}{f-n}\right)n\&= -\frac{2fn}{f-n}
\end{aligned}
\end{equation}
\]
有了A和B,则\(z_e\)和\(z_n\)之间的关系表达式为:
\[ \begin{equation} \begin{aligned} z_n = \frac{-\frac{f+n}{f-n}z_e - \frac{2fn}{f-n}}{-z_e} &\quad (3) \end{aligned} \end{equation} \]
最后,完整的投影矩阵为:
\[ \left( \begin{matrix} \frac{2n}{r-l} & 0 & \frac{r+l}{r-l} & 0\0 & \frac{2n}{t-b} & \frac{t+b}{t-b} & 0\0 & 0 & \frac{-(f+n)}{f-n} & \frac{-2fn}{f-n}\0 & 0 & -1 & 0 \end{matrix} \right) \]
上面这是一个通用视景体的投影矩阵。当视景体是对称时,即r=-l, t=-b,则:
\[
\begin{equation}
\left\{
\begin{array}{lr}
r+l=0\r-l=2r
\end{array}
\right.
\end{equation}
\]
\[ \begin{equation} \left\{ \begin{array}{lr} t+b=0\t-b=2t \end{array} \right. \end{equation} \]
故投影矩阵可以简化为:
\[ \left( \begin{matrix} \frac{n}{r} & 0 & 0 & 0\0 & \frac{n}{t} & 0 & 0\0 & 0 & \frac{-(f+n)}{f-n} & \frac{-2fn}{f-n}\0 & 0 & -1 & 0 \end{matrix} \right) \]
透视投影矩阵我们已经求出来了,在继续往下探讨之前,请再看一下上面的方程(3),即:
\[ \begin{equation} \begin{aligned} z_n = \frac{-\frac{f+n}{f-n}z_e - \frac{2fn}{f-n}}{-z_e} &\quad (3) \end{aligned} \end{equation} \]
可以看到它是一个有理函数(rational function),且是一个非线性函数。这意味着在近裁剪面(near plane)附近,它具有很高的精度(very high precision),而在远裁剪面(far plane)附近具有非常小的精度(very little precision)。如果[-n, -f]的范围比较大,它会造成深度值精度问题(z-fighting),即可能在离far plane比较近的地方,当\(z_e\)的值差异较小时,它们对应的\(z_n\)值相同,或者说当一个\(z_e\)值发生小的变化时,对应的\(z_n\)不受影响(即值不变)。这会产生错误的视觉效果。如下面图7所示,在远裁剪面附近,\(z_n\)的值几乎不随\(z_e\)发生变化。
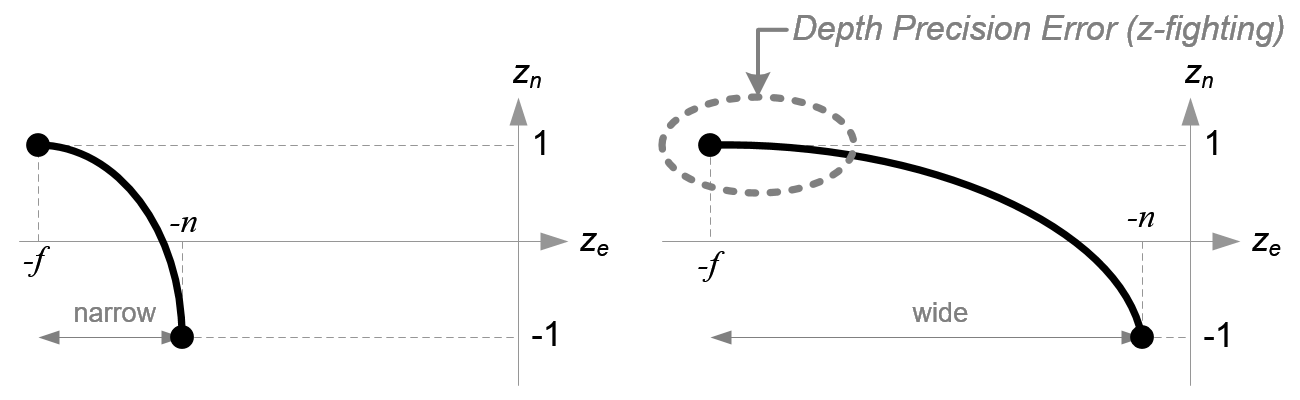
(图7. 深度缓存的精度比较)
一些避免z-fighting的方法:
构建正交投影矩阵相对来说会简单一些。
(图8. 正交投影视景体及对应的NDC)
在eye space中,所有\(x_e, y_e, z_e\)分量是线性映射到NDC中的。我们只需要把一个长方体(rectangular volume)所表达的体积缩放成一个立方体(cube),并把它移动到原点(如图8)。下面我们将使用线性映射关系(linear relationship)来找到正交投影矩阵的各个元素。
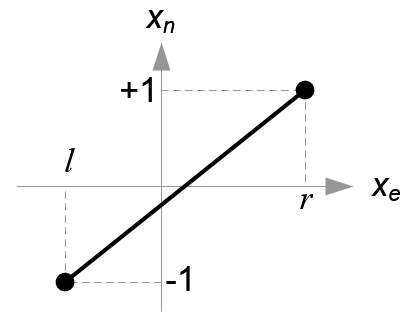
(图9. 把\(x_e\)映射到\(x_n\))
\[ \begin{equation} \begin{aligned} x_n &= \frac{1-(-1)}{r-l}\cdot x_e + \beta\1&=\frac{2r}{r-l} + \beta, (substitute (r, 1) for (x_e, x_n))\\beta &= 1 - \frac{2r}{r-l}=-\frac{r+l}{r-l}\\therefore x_n &= \frac{2}{r-l}\cdot x_e - \frac{r+l}{r-l} \end{aligned} \end{equation} \]
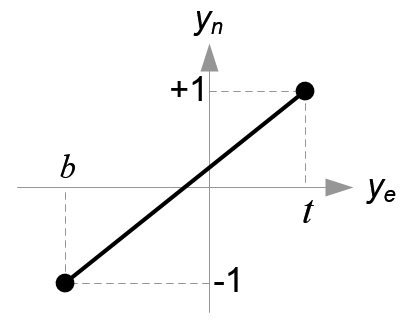
(图10. 把\(y_e\)映射到\(y_n\))
\[ \begin{equation} \begin{aligned} y_n &= \frac{1-(-1)}{t-b}\cdot y_e + \beta\1 &= \frac{2t}{t-b}+\beta, (substitute (t, 1) for (y_e, y_n))\\beta &= 1 - \frac{2t}{t-b} = -\frac{t+b}{t-b}\\therefore y_n &= \frac{2}{t-b}\cdot y_e - \frac{t+b}{t-b} \end{aligned} \end{equation} \]
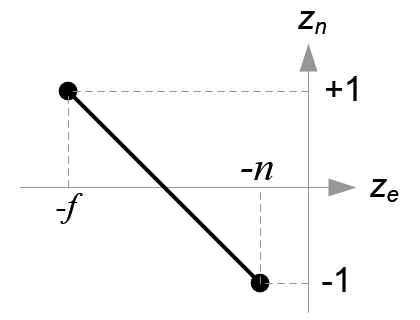
(图11. 把\(z_e\)映射到\(z_n\))
\[ \begin{equation} \begin{aligned} z_n &= \frac{1-(-1)}{-f-(-n)}\cdot z_e + \beta\1 &=\frac{2f}{f-n} + \beta, (substitute (-f, 1) for (z_e, z_n))\\beta &= 1 - \frac{2f}{f-n}=-\frac{f+n}{f-n}\\therefore z_n &= \frac{-2}{f-n}\cdot z_e - \frac{f+n}{f-n} \end{aligned} \end{equation} \]
因为对于正交投影w分量不是必须的,所以正交投影矩阵的第4行为(0, 0, 0, 1)。因此完整的正交投影矩阵为:
\[ \left( \begin{matrix} \frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l}\0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b}\0 & 0 & \frac{-2}{f-n} & -\frac{f+n}{f-n}\0 & 0 & 0 & 1 \end{matrix} \right) \]
如果视景体对称的话,即r=-l, t=-b, 则:
\[ \begin{equation} \left\{ \begin{array}{lr} r+l=0 \r-l=2r \end{array} \right. \end{equation} \]
\[ \begin{equation} \left\{ \begin{array}{lr} t+b=0 \t-b=2r \end{array} \right. \end{equation} \]
故正交投影矩阵被简化为:
\[
\left(
\begin{matrix}
\frac{1}{r} & 0 & 0 & 0\0 & \frac{1}{t} & 0 & 0\0 & 0 & \frac{-2}{f-n} & -\frac{f+n}{f-n}\0 & 0 & 0 & 1
\end{matrix}
\right)
\]
首发于我的知乎专栏
References:
OpenGL投影矩阵(Projection Matrix)构造方法
标签:vol 相对 ati href poi 缓存 依赖 nal tran
原文地址:https://www.cnblogs.com/leixinyue/p/11166135.html