标签:添加 大于 依次 插入数据 code http 解决 ima 构造方法
前面有学习过二叉树,二叉搜索树(也叫做二叉查找树或者二叉排序树)也是一种二叉树,主要其搜索速度非常快,接下来了解一下。
(1)如果左子树不为空,则左子树上的结点的值都小于根结点
(2)如果右子树不为空,则右子树上的结点的值都大于根结点
(3)子树同样满足上述两点
如下就是一颗典型的二叉搜索树,可以看出从根结点‘5‘开始,左子结点为‘3‘,右子结点为‘8‘,满足上述规则,然后以‘3‘为根结点,依然符合上述规则,其他也均符合。二叉搜索树的查找速度是非常快的,其时间复杂度就是二叉树的深度,通过下图很好理解,查找一个数最多就是查询到叶子结点,其次数就是二叉树的深度,因此时间复杂度为O(logn)。
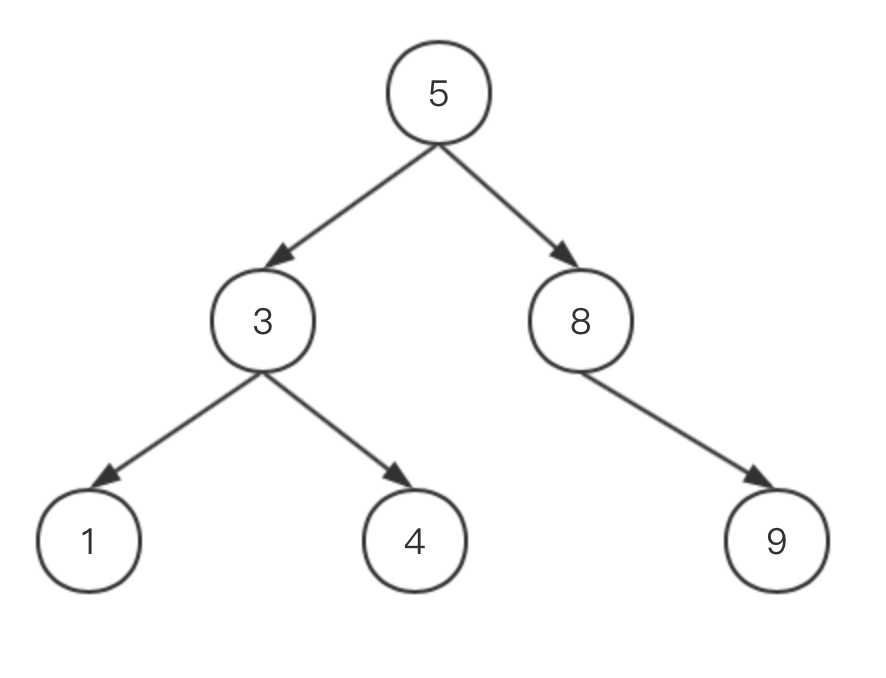
有趣的是,将上面这棵二叉搜索树进行中序遍历,发现结果为1,3,4,5,8,9,其恰好是一个排序好的顺序,因此二叉搜索树也叫做二叉排序树。
在了解了二叉树的特点后,如果给一串数字,如何用代码将其存入二叉树呢。其实在了解了上面的特点后,使用递归的方法就能写出实现代码。
1 /** 2 * 二叉搜索树 3 */ 4 public class BinarySearchTree { 5 //定义属性 6 private int data;//数据 7 private BinarySearchTree left;//左子树 8 private BinarySearchTree right;//右子树 9 10 //构造方法 11 public BinarySearchTree(int data, BinarySearchTree left, BinarySearchTree right) { 12 this.data = data; 13 this.left = left; 14 this.right = right; 15 } 16 17 //插入一个数字到结点 18 public static void insert(BinarySearchTree root,int number) { 19 //插入到左子树 20 if (number < root.data) { 21 //如果左子树没有 22 if (root.left == null) { 23 root.left = new BinarySearchTree(number, null, null); 24 } 25 //如果左子树有结点,将左子树起始结点作为根结点接续执行插入逻辑 26 if(root.left!=null){ 27 insert(root.left,number); 28 } 29 } 30 //插入到右子树 31 if(number>root.data){ 32 //如有右子树没有 33 if(root.right==null){ 34 root.right=new BinarySearchTree(number,null,null); 35 } 36 //如果右子树有结点,将右子树起始结点作为根结点接续执行插入逻辑 37 if(root.right!=null){ 38 insert(root.right,number); 39 } 40 } 41 42 } 43 //使用中序遍历输出排序结果,使用了递归 44 public static void in(BinarySearchTree node){ 45 //左子树→根结点→右子树 46 if(node.left!=null){ 47 in(node.left); 48 } 49 System.out.print(node.data+","); 50 if(node.right!=null){ 51 in(node.right); 52 } 53 } 54 //测试 55 public static void main(String[] args) { 56 int[] data=new int[]{55,200,25,32,17,67,300}; 57 //将数组第一个元素作为根结点 58 BinarySearchTree tree=new BinarySearchTree(data[0],null,null); 59 //开始插入数组到二叉搜索树 60 for (int i = 1; i < data.length; i++) { 61 tree.insert(tree,data[i]); 62 } 63 //使用中序遍历输出 64 in(tree); 65 } 66 }
控制台输出情况,可以看出数字能正常插入二叉树,并使用中序遍历可输出排序后的数组。

以上面这个数组为例,如果要查找9,需要查找多少次呢?首先是从根结点进入,然后依次进行如下判断:
(1)9比5大,因此进入右边子树找到8
(2)9比8大,因此进入右边子树找到9,这样就找到了,结束查找
发现只需要找2次就可以找到需要数字,如果遍历的话最多需要5次,当一个数组非常大的时候,二叉搜索树的查找优势就明显体现出来,如下例。
问题:如果上述数组的大小是一个20亿长度大小的数组,要找到一个数最多需要多少次呢?
分析:假设这20亿个数组成了一个满平衡二叉树,先计算一下这棵数的深度,就可以判断出最多需要找多少次了。
解决过程:参考上篇博客,如果是n个结点的满二叉树计算深度,可以假设深度为x,这样2^x-1=n,然后得到2^x=n+1,最后得到深度x=log2^(n+1),所以深度等于log2^(20亿),由于2^32约等于21亿,因此深度约等于32,在理想情况下只需要32次就可以找到了。在极端的情况下,如下图所示当二叉树退化成一个链表时,这样最多需要寻找20亿次,这种情况需要使用平衡二叉树来存储数据会更好,平衡二叉树在插入数据的时候还有左旋和右旋动作,会让树形结构左右更加平衡。
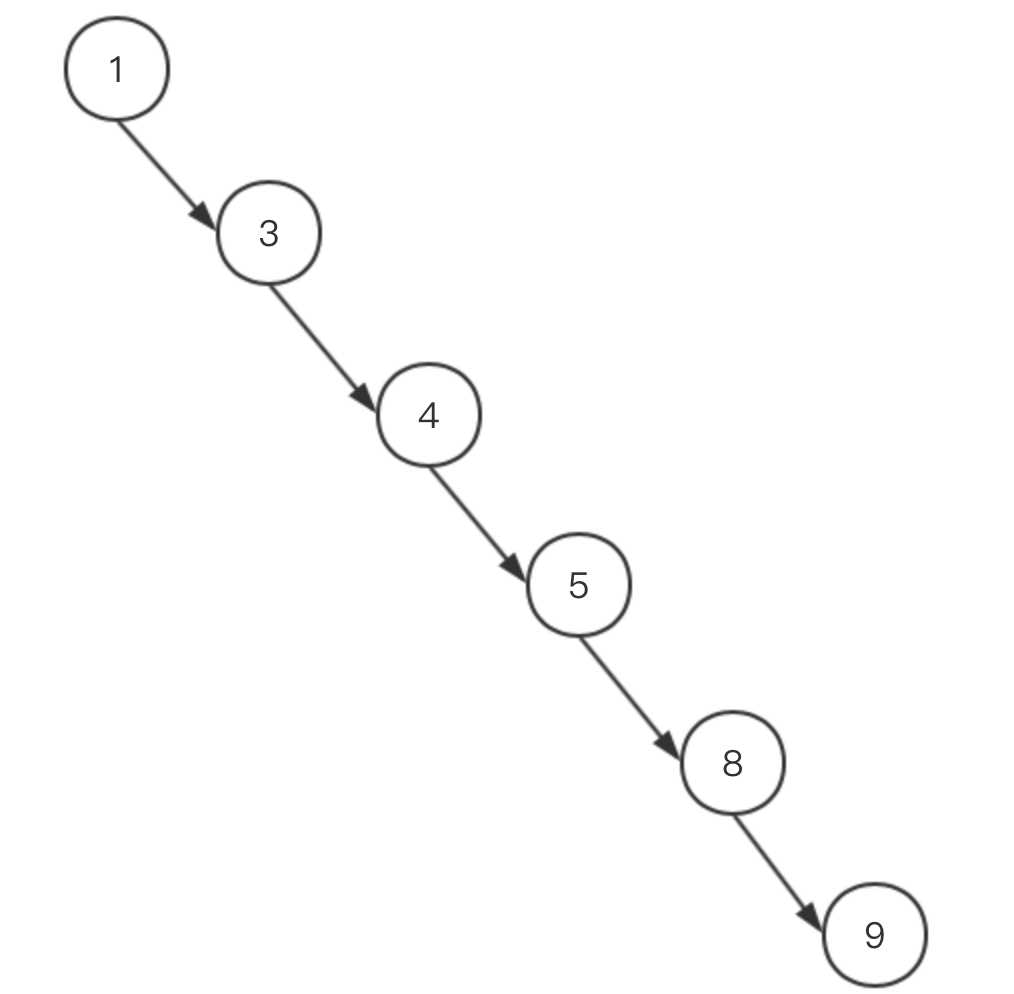
如果是二叉搜索树来查找数据,用代码如何来实现呢,其实也是需要用到递归,先写一段逻辑完成对一个结点的比较查询,然后将新找到的子树顶端结点作为根结点继续查找,在上面代码中添加如下方法。
1 //从根结点进入二叉树,开始查找一个数 2 public static void find(BinarySearchTree root,int number){ 3 //先和根结点数字进行比较 4 if(root.data==number){ 5 System.out.println("二叉树中查找到了数字"+number); 6 } 7 //进入左子树查找 8 if(number<root.data){ 9 if(root.left==null){ 10 System.out.println("左子树没有这个数"); 11 }else{ 12 find(root.left,number); 13 } 14 } 15 //进入右子树查找 16 if(number>root.data){ 17 if(root.right==null){ 18 System.out.println("右子树没有这个数"); 19 }else{ 20 find(root.right,number); 21 } 22 } 23 }
测试代码,在二叉树中查找55,17,200三个数。
1 public static void main(String[] args) { 2 int[] data=new int[]{55,200,25,32,17,67,300}; 3 //将数组第一个元素作为根结点 4 BinarySearchTree tree=new BinarySearchTree(data[0],null,null); 5 //开始插入数组到二叉搜索树 6 for (int i = 1; i < data.length; i++) { 7 tree.insert(tree,data[i]); 8 } 9 //使用中序遍历输出 10 in(tree); 11 //查找某个数 12 System.out.println(); 13 find(tree,55); 14 find(tree,17); 15 find(tree,301); 16 }
控制台输出情况,发现可以正常得到结果。

二叉搜索树是一种查询速度非常快的排序树,其根据根结点的选择,可能是平衡树也可能是非平衡树,在非平衡的情况下查找可能退化成链表,理想情况下查询次数非常少。
标签:添加 大于 依次 插入数据 code http 解决 ima 构造方法
原文地址:https://www.cnblogs.com/youngchaolin/p/11175877.html