标签:部分 open 复制 思想 区间 style 输入格式 clu ora
现在有一堆数字共N个数字(N<=10^6),以及一个大小为k的窗口。现在这个从左边开始向右滑动,每次滑动一个单位,求出每次滑动后窗口中的最大值和最小值。
例如:
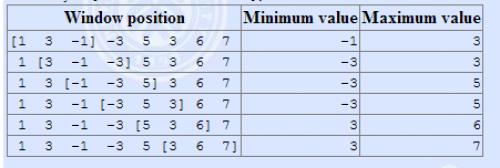
The array is [1 3 -1 -3 5 3 6 7], and k = 3.
输入一共有两行,第一行为n,k。
第二行为n个数(<INT_MAX).
输出格式:输出共两行,第一行为每次窗口滑动的最小值
第二行为每次窗口滑动的最大值
50%的数据,n<=10^5
100%的数据,n<=10^6
【解题思路】
一道单调队列的经典题了,今天来发一篇题解:
这里有两部分代码相似,分别是求下降栈和上升栈
首先要初始化head=1,tail=0表示当前队列为空
以单调下降栈为例:
则我们可知当我们把区间(l,r)移动到(l+1,r+1)如果队首元素不在(l+1,r+1)中,删除它将a[r+1]插入队列这样处理后的队首元素便是最大值
入栈(队列)的时候要判断栈顶是否与插入的元素符合大小关系,否则出栈顶直到满足要求
这也单调队列很重要的思想
其余同理
【code】
1 #include <cstdio> 2 #include <deque> 3 #include <algorithm> 4 using namespace std; 5 const int N=1000005; 6 int i,n,k,a[N],q[N],num[N]; 7 int head,tail; 8 int f1[N],f2[N]; 9 int main(){ 10 //freopen("window.in","r",stdin); 11 //freopen("window.out","w",stdout); 12 scanf("%d%d",&n,&k); 13 for (register int i=1;i<=n;i++) 14 scanf("%d",&a[i]); 15 head=1; 16 tail=0; 17 for (register int i=1;i<=n;i++){ 18 while(num[head]<i-k+1&&head<=tail)head++; 19 while(a[i]<q[tail]&&head<=tail)tail--; 20 num[++tail]=i; 21 q[tail]=a[i]; 22 f1[i]=q[head]; 23 } 24 head=1; 25 tail=0; 26 for (register int i=1;i<=n;i++){ 27 while(num[head]<i-k+1&&head<=tail)head++; 28 while(a[i]>=q[tail]&&head<=tail)tail--; 29 num[++tail]=i; 30 q[tail]=a[i]; 31 f2[i]=q[head]; 32 } 33 for(register int i=k;i<=n;i++) 34 printf("%d ",f1[i]); 35 printf("\n"); 36 for(register int i=k;i<=n;i++) 37 printf("%d ",f2[i]); 38 printf("\n"); 39 return 0; 40 }
标签:部分 open 复制 思想 区间 style 输入格式 clu ora
原文地址:https://www.cnblogs.com/66dzb/p/11192676.html