【信息学奥赛一本通提高组】第二章二分与三分

　　二分法，在一个单调有序的集合或函数中查找一个解，每次分为左右两部分，判断解在那个部分并调整上下界，直到找到目标元素，每次二分都将舍弃一般的查找空间，因此效率很高。

二分常见模型

　　最小值最大（或是最大值最小）问题，这类双最值问题常常选用二分法求解，也就是确定答案后，配合贪心，DP等其他算法检验这个答案是否合理，将最优化问题转化为判定性问题。例如，将长度为n的序列ai分为最多m个连续段，求所有分法中每段和的最大值的最小是多少？

　　用具有单调性的布尔表达式求解分界点，比如在有序数列中求数字x的排名。

　　有时，对于一些单峰函数，我们可以用二分导函数的方法求解函数的极值，这时通常将函数的定义域定义为整数域求解比较方便，此时dx可以直接去整数1。

二分写法

版本1
当我们将区间[l, r]划分成[l, mid]和[mid + 1, r]时，其更新操作是r = mid或者l = mid + 1;，计算mid时不需要加1。

版本2
当我们将区间[l, r]划分成[l, mid - 1]和[mid, r]时，其更新操作是r = mid - 1或者l = mid;，此时为了防止死循环，计算mid时需要加1。

　　5、如果更新方式是 L = Mid ， R = Mid - 1 ，那么在算mid时要加1

【例题1】愤怒的牛

题目描述

农夫约翰建造了一座有n间牛舍的小屋，牛舍排在一条直线上，第i间牛舍在xi的位置，但是约翰的m头牛对小屋很不满意，因此经常互相攻击。约翰为了防止牛之间互相伤害，因此决定把每头牛都放在离其它牛尽可能远的牛舍。也就是要最大化最近的两头牛之间的距离。
牛们并不喜欢这种布局，而且几头牛放在一个隔间里，它们就要发生争斗。为了不让牛互相伤害。John决定自己给牛分配隔间，使任意两头牛之间的最小距离尽可能的大，那么，这个最大的最小距离是多少呢？

输入

第一行用空格分隔的两个整数n和m；
第二行为n个用空格隔开的整数，表示位置xi。

输出

输出仅一个整数，表示最大的最小距离值。

样例输入

样例输出

提示

把牛放在1,4,8这样最小距离是3

2≤n≤1e5 , 0≤xi≤1e9, 2≤m≤n

【思路】：

　　类似的最大值最小化问题，通常用二分法就可以很快地解决。我们定义：

　　设C(d)表示可以安排牛的位置，并使得最近的两头牛的距离不小于d。

　　那么问题就转换为求满足C(d)的最大的d，另外，最近的间距不小于d也可以看成是所有牛的间距都小于d，因此就可以用C(d)表示可以安排牛的位置，并使得任意的两头牛的距离不小于d。

　　对于这个问题的判断，使用贪心法便可非常容易地求解

　　1、对牛舍的位置x进行排序。

　　2、把第一头牛放入x0的牛舍。

　　3、如果第i头牛放入了xj间牛舍，则第i+1头牛就要放入满足xj+d<=xk的最小牛舍xk中。

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 typedef long long ll;
 4 const int N = 1e5+100;
 5 const ll Inf = (1ll<<20);
 6 ll a[N],A,B;
 7 bool check(ll x){
 8     ll tot = 1 ;
 9     ll pre = 0;
10     for(int i=1;i<A;i++){
11         if( a[i] - a[pre] >= x ){
12             pre = i;
13             tot++;
14         }
15     }
16     if( tot >= B ) return true;
17     else           return false;
18 }
19 int main()
20 {
21     ll L = 1, R = 0 , mid , ans = 0 ;
22     scanf("%lld%lld",&A,&B);
23     for(int i=0;i<A;i++){
24         scanf("%lld",&a[i]);
25     }
26     sort( a , a+A );
27     R = a[A-1] - a[0] ;
28     while( L<=R ){
29         mid = (L+R) >> 1 ;
30         if( check( mid ) ){
31             ans = mid ;
32             L = mid + 1 ;
33         }else{
34             R = mid - 1 ;
35         }
36     }
37     return 0*printf("%lld\n",ans);
38 }

愤怒的牛

【例题2】Best Cow Fences

题目描述

给定一个长度为n的正整数序列A，求一个平均数最大的，长度不小于L的子段。

输入

第一行用空格分隔的两个整数n和L；
第二行为n个用空格隔开的整数，表示Ai。

输出

输出一个整数，表示答案的1000倍。不用四舍五入，直接输出。

样例输入

10 6
6 4 2 10 3 8 5 9 4 1

样例输出

提示

1≤n≤1e5 , 1≤Ai≤2000

【注意】：这里指的序列并不是（我们字符串的序列，好比最长上升子序列），而是（子串）性的序列。

【思路】：

　　二分结果，判断“是否存在一个长度不小于L的子序列，平均数不小于二分的值”

　　如果把数列中每个数都减去二分的值，就转化为判定“是否存在一个长度不小于的L的子序列，子序列的和非负”。

　　下面着重解决两个问题：

　　1、求一个子序列，它的和最大，没有“长度不小于L”的限制

　　无长度限制的最大子序列和问题是一个经典的问题，只需O(n)扫描该数列，不断地把新的数加入子序列，当子序列和变成负数时，把当前整个子序列清空，扫描过程中出现过的最大子序列和即为所求。

　　2、求一个子序列，它的和最大，子序列的长度不小于L。

　　子序列和可以转化为前缀和相减的形式，即设sum_i 表示 A1~Ai的和，则有：

　　max i-j >=t { Aj+1+Aj+2+……+Ai } = max L <= i <= n { sum - min 0<= j <= i-L {sum j } }

　　仔细观察上面的式子可以发现，随着i的增长，j的取值范围0~i-L每次只会增加1。换而言之，每次只会有一个新的值假如min{sum j }的候选集合，所以我们没有必要每次循环枚举j次，只需要用一个变量记录当前最小值，每次与新的取值sum i-L 取min就可以了。

　　解决问题2后，我们只需要判断最大子序列和是不是非负数,就可以确定二分上下界的变化范围了。

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 const int N = 1e5+10 ;
 4 const double eps = 1e-6 ;
 5 typedef long long ll;
 6 double a[N],b[N],sum[N];
 7 int n,m;
 8 void Input(){
 9     cin >> n >> m ;
10     for ( int i=1 ; i<=n ; i++ ){
11         cin >> a[i] ;
12     }
13 }
14 int main()
15 {
16     ios_base :: sync_with_stdio(0) ;
17     cin.tie(NULL) ; cout.tie(NULL) ;
18 
19     Input() ;
20 
21     double L = -1e6 , R = 1e6 , Mid , Ans , Minz ;
22     while ( R-L > eps ){
23         Mid = (L+R) / 2 ;
24         for ( int i = 1 ; i<=n ; i++ ) {
25             b[i] = a[i] - Mid ;
26             sum[i] = sum[i-1] + b[i] ;
27         }
28         Ans = -1e10 ;
29         Minz = 1e10 ;
30         for ( int i = m ; i<=n ; i++ ){
31             Minz = min( Minz , sum[i-m] );
32             Ans = max ( Ans , sum[i] - Minz ) ;
33         }
34         if ( Ans >= 0 ) L = Mid  ;
35         else R = Mid ;
36     }
37     cout << int ( R * 1000 ) << endl ;
38     return 0;
39 }

Best Cow Fences

二、三分

　　三分法适用于求解凸性函数的极值问题，二次函数就是一个典型的单峰函数。

　　三分法与二分法一样，它会不断缩小答案所在的求解区间，二分法缩小区间利用的原理是函数的单调性，而三分法利用的则是函数的单峰性。

　　设当前求解的区间为[L,R]，令 m1 = L + (R-L) / 3 ，m2 = R - (R-L) / 3 ，接着我们计算这两个点的函数值f(m1),f(m2),之后我们将两点中函数值更优的那个点成为好点（若计算最大值，则f更大的那个点就为好点，计算最小值同理），而函数值较差的那个点就称为坏点。

　　我们可以证明，最优点可能会与好点或坏点同侧。

　　如m1是好点，则m2是坏点。

　　因此，最后的最优点会与m1 与m2的左侧，即我们求解的区间由 [L,R] 变为 [ L,m2 ] ，因此根据这个结论我们可以不停缩小求解区间，直到求出近似值。

1 double L = 0 , R = 1e9 ;
2 while ( R - L <= 1e-3 ){
3     double M1 = L + (R-L)/3 ;
4     double M2 = R - (R-L)/3 ;
5     if ( F(M1) < F(M2) )    
6         L = M1 ;
7     else
8         R = M2 ;
9 }

三分写法

【例题3】曲线(curves)

题目描述

明明做作业的时候遇到了n个二次函数Si(x)=ax2+bx+c，他突发奇想设计了一个新的函数F(x)=max{Si(x)},i=1…n。

明明现在想求这个函数在[0,1000]的最小值，要求精确到小数点后四位，四舍五入。

输入

输入包含T组数据，每组第一行一个整数n；
接下来n行，每行3个整数a,b,c，用来表示每个二次函数的3个系数。注意：二次函数有可能退化成一次。

输出

每组数据输出一行，表示新函数 F(x)的在区间 [0,1000]上的最小值。精确到小数点后四位，四舍五入。

样例输入

样例输出

0.0000
0.5000

提示

对于50%的数据，1≤n≤100；
对于100%的数据，1≤T≤10,1≤n≤1e5,0≤a≤100, 0≤∣b∣≤5000,0≤∣c∣≤5000。

【思路】

　　由于函数S是开口向上的二次函数(当a=0时，是一次函数)，由S的定义可知，S或者是一个先单调减、后单调增的下凸函数，或者是一个单调函数，F(x)=max(S(x))也满足单调性。选用三分法很容易求得某个区间内的最小值。

【代码】：

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 const int N = 1e4+100;
 4 const double EPS = 1e-11 ;
 5 int n;
 6 double a[N],b[N],c[N];
 7 double F(double x) {
 8     double maxz = -0x7fffffff;
 9     for ( int i=1 ; i<=n ; i++ ){
10         maxz = max ( maxz , a[i]*x*x + b[i]*x + c[i] );
11     }
12     return maxz ;
13 }
14 int main(){
15     int T ;
16     scanf("%d",&T);
17     while(T--){
18         scanf("%d",&n);
19         for(int i=1;i<=n;i++){
20             scanf("%lf%lf%lf",&a[i],&b[i],&c[i]);
21         }
22         double L = 0 , R = 1000, Lmid , Rmid ;
23         while ( R - L > EPS ) {
24             Lmid = L + (R-L) / 3 ;
25             Rmid = R - (R-L) / 3 ;
26             if ( F(Lmid) <= F(Rmid) ){
27                 R = Rmid ;
28             }else{
29                 L = Lmid ;
30             }
31         }
32         printf("%.4f\n",F(L) ) ;
33     }
34     return 0 ;
35 }

曲线

【习题1】数列分段

题目描述

对于给定的一个长度为N的正整数数列A，现要将其分成M段，并要求每段连续，且每段和的最大值最小。
例如，将数列4 2 4 5 1要分成3段：
若分为[4 2][4 5][1]，各段的和分别为6,9,1，和的最大值为9；
若分为[4][2 4] [5 1]，各段的和分别为4,6,6，和的最大值为6；
并且无论如何分段，最大值不会小于6。
所以可以得到要将数列4 2 4 5 1要分成3段，每段和的最大值最小为6。

输入

第1行包含两个正整数N，M；
第2行包含N个空格隔开的非负整数Ai，含义如题目所述。

输出

仅包含一个正整数，即每段和最大值最小为多少。

样例输入

5 3
4 2 4 5 1

样例输出

提示

对于100%的数据，有N≤106，M≤N，Ai之和不超过109

【思路】

这个题目类似与愤怒的牛，求最大值的最小值，

二分答案，然后判断是否正确。

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 typedef long long ll;
 4 const int N = 1e5+100;
 5 ll a[N],n,m;
 6 bool check ( ll x ){
 7     int cnt = 1 ;
 8     ll sum = 0;
 9     for (int i=1;i<=n;i++){
10         if ( sum + a[i] > x ){
11             cnt ++ ;
12             sum = a[i] ;
13         }else{
14             sum += a[i] ;
15         }
16     }
17     return cnt <= m ;
18 }
19 int main()
20 {
21     ll L = -0x7fffffff , R = 0 ;
22     scanf("%lld%lld",&n,&m);
23     for(int i=1;i<=n;i++){
24         scanf("%lld",&a[i]);
25         L = max ( a[i],L) ;
26         R += a[i] ;
27     }
28     ll  mid , ans ;
29     while( L<=R ){
30         mid = L+R >> 1 ;
31         if( check(mid) ){
32             R = mid - 1 ;
33             ans = mid ;
34         }else{
35             L = mid + 1 ;
36         }
37     }
38     printf("%lld\n",ans);
39     return 0;
40 }

数列分段

【习题2】扩散

题目描述

一个点每过一个单位时间就会向4个方向扩散一个距离，如图所示：两个点a、b连通，记作e(a,b)，当且仅当a、b的扩散区域有公共部分。连通块的定义是块内的任意两个点u、v都必定存在路径
e(u,a0),e(a0,a1),…e(ak,v)。
给定平面上的n个点，问最早什么时候它们形成一个连通块。

输入

第一行一个数n，以下n行，每行一个点坐标。

输出

输出仅一个数，表示最早的时刻所有点形成连通块。

样例输入

2
0 0
5 5

样例输出

提示

对于100%的数据，满足1≤n≤50,1≤Xi,Yi≤1e9。

【思路】：

　　这个题目其实用了两方面：

　　1、连通块需要用并查集来完成。

　　2、一个点的扩散，就像一个菱形在坐标外扩散，然后只有当两个点在t时间后相通即为：曼哈顿距离小于等于2t。

【代码】：

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 typedef long long ll;
 4 const int N = 55;
 5 ll x[N],y[N];
 6 int pre[N];
 7 int Find(int x){
 8     return pre[x] = ( x==pre[x] ? x : Find(pre[x]) );
 9 }
10 int n;
11 void Init(){
12     scanf("%d",&n);
13     for(int i=1;i<=n;i++){
14         scanf("%lld%lld",&x[i],&y[i]) ;
15     }
16 }
17 int vis[55];
18 bool check(ll val){
19     int cnt = 0 ;
20     memset ( vis, 0 , sizeof vis );
21 
22     for (int i=1 ;i<=n;i++) pre[i] = i ;
23     for(int i=1;i<=n;i++){
24         for(int j=i+1;j<=n;j++){
25             if( abs(x[i]-x[j]) + abs(y[i]-y[j]) <= 2*val ){
26                 int Fu = Find(i) ;
27                 int Fv = Find(j) ;
28                 if( Fu != Fv ) {
29                     pre[Fv] = Fu ;
30                 }
31             }
32         }
33     }
34 
35     for(int i=1;i<=n;i++){
36         cnt += (pre[i]==i);
37     }
38     return cnt == 1 ;
39 }
40 int main()
41 {
42     Init();
43     ll L = 0 , R = 1e9 , Mid ,ans =0 ;
44     while ( L<=R ){
45         Mid = L+R >> 1 ;
46         if ( check(Mid) ){
47             R = Mid  - 1 ;
48             ans = Mid ;
49         }else{
50             L = Mid  + 1 ;
51         }
52     }
53     printf("%lld\n",ans );
54     return 0;
55 }
56 /*
57 
58 5
59 5 5
60 7 8
61 6 8
62 5 8
63 4 6
64 
65 */

扩散

【习题3】灯泡（ZOJ 3203）

题目描述

相比 wildleopard 的家，他的弟弟 mildleopard 比较穷。他的房子是狭窄的而且在他的房间里面仅有一个灯泡。每天晚上，他徘徊在自己狭小的房子里，思考如何赚更多的钱。有一天，他发现他的影子的长度随着他在灯泡和墙壁之间走到时发生着变化。一个突然的想法出现在脑海里，他想知道他的影子的最大长度。
技术图片

输入

第一行包含一个整数T，表示测试数据的组数。
对于每组测试数据，仅一行，包含三个实数H，h和D，H表示灯泡的高度，h表示mildleopard的身高，D表示灯泡和墙的水平距离。

输出

共T行，每组数据占一行表示影子的最大长度，保留三位小数。

样例输入

样例输出

1.000
0.750
4.000

提示

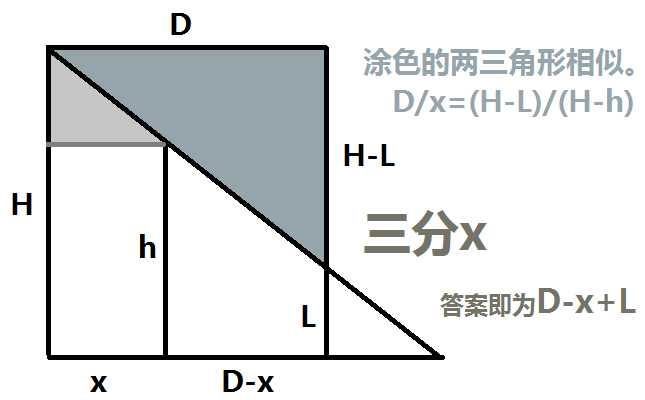
T≤100，10^−2≤H,h,D≤1e3，10^−2≤H−h

【题解】

　　技术图片

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 typedef long long ll;
 4 const double eps = 1e-7;
 5 double H,h,D;
 6 double F(double x){
 7     double L = H - (H-h)*D / x ;
 8     return D-x+L;
 9 }
10 int main()
11 {
12     int T;
13     scanf("%d",&T);
14     while(T--){
15         scanf("%lf%lf%lf",&H,&h,&D);
16         double L = D*(H-h)/H , R = D ;
17         while ( R-L >= eps ){
18             double Lmid = L + (R-L)/3 ;
19             double Rmid = R - (R-L)/3 ;
20             if ( F(Lmid) <= F(Rmid) ){
21                 L = Lmid ;
22             }else{
23                 R = Rmid ;
24             }
25         }
26         printf("%.3f\n",F(L));
27     }
28     return 0 ;
29 }

灯泡

【习题4】传送带

题目描述

在一个2维平面上有两条传送带，每一条传送带可以看成是一条线段。两条传送带分别为线段AB和线段CD。lxhgww在AB上的移动速度为P，在CD上的移动速度为Q，在平面上的移动速度R。现在lxhgww想从A点走到D点，他想知道最少需要走多长时间

输入

第一行是4个整数，表示A和B的坐标，分别为Ax，Ay，Bx，By
第二行是4个整数，表示C和D的坐标，分别为Cx，Cy，Dx，Dy
第三行是3个整数，分别是P，Q，R

输出

一行，表示lxhgww从A点走到D点的最短时间，保留到小数点后2位

样例输入

0 0 0 100
100 0 100 100
2 2 1

样例输出

136.60

提示

对于100%的数据，1<= Ax，Ay，Bx，By，Cx，Cy，Dx，Dy<=1000，1<=P，Q，R<=10

技术图片

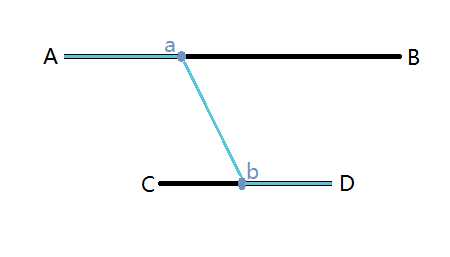
【题解】：

　　分三部分来计算，三分套三分，第一个三分是分AB段的，第二个三分是分CD段的，用百分比来进行三分，最后得到的点连接。

　　个人感觉这个题目写倒不是什么问题，关键是可能没想出来还能这样用百分比来写。

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 const double eps = 1e-6;
 4 double Ax,Ay,Bx,By,Cx,Cy,Dx,Dy ;
 5 double P , Q , R ;
 6 typedef struct node{
 7     double x,y;
 8 }point ;
 9 point A,B,C,D,p1,p2;
10 double dis ( point u , point v ){
11     return sqrt( (u.x - v.x)*(u.x - v.x) +
12                  (u.y - v.y)*(u.y - v.y) ) ;
13 }
14 double Cal ( double u , double v ){
15     p1.x = Ax + (Bx-Ax)*u  ;
16     p1.y = Ay + (By-Ay)*u  ;
17 
18     p2.x = Cx + (Dx-Cx)*v  ;
19     p2.y = Cy + (Dy-Cy)*v  ;
20 
21     return dis(A,p1) / P + dis(p1,p2) / R + dis(p2,D) /Q  ;
22 }
23 double F (double u) {
24     double L = 0 , R = 1 ;
25     double Lmid ,Rmid ;
26     while ( R-L >= eps ){
27         Lmid = L + ( R-L )/3 ;
28         Rmid = R - ( R-L )/3 ;
29         if( Cal(u,Lmid) <= Cal(u,Rmid) ){
30             R = Rmid ;
31         }else{
32             L = Lmid ;
33         }
34     }
35     return Cal(u,L);
36 }
37 int main()
38 {
39     ios_base :: sync_with_stdio(0) ;
40     cin.tie(NULL) ;
41     cout.tie(NULL);
42 
43     cin >> Ax >> Ay >> Bx >> By >> Cx >> Cy >> Dx >> Dy ;
44     cin >> P >> Q >> R ;
45     A.x = Ax ;  A.y = Ay ;
46     B.x = Bx ;  B.y = By ;
47     C.x = Cx ;  C.y = Cy ;
48     D.x = Dx ;  D.y = Dy ;
49     double L = 0 , R = 1 ;
50     double Lmid ,Rmid ;
51     while ( R-L >= eps ){
52         Lmid = L + ( R-L )/3 ;
53         Rmid = R - ( R-L )/3 ;
54         if( F(Lmid) <= F(Rmid) ){
55             R = Rmid ;
56         }else{
57             L = Lmid ;
58         }
59     }
60     printf("%.2f\n",F(L));
61     return 0;
62 }

传送带

【信息学奥赛一本通 提高组】第二章 二分与三分

一、二分

二分常见模型

二分写法

【例题1】愤怒的牛

题目描述

输入

输出

样例输入

样例输出

提示

【例题2】Best Cow Fences

题目描述

输入

输出

样例输入

样例输出

提示

二、三分

【例题3】曲线(curves)

题目描述

输入

输出

样例输入

样例输出

提示

【习题1】数列分段

题目描述

输入

输出

样例输入

样例输出

提示

【习题2】扩散

题目描述

输入

输出

样例输入

样例输出

提示

【习题3】灯泡（ZOJ 3203）

题目描述

输入

输出

样例输入

样例输出

提示

【习题4】传送带

题目描述

输入

输出

样例输入

样例输出

提示

【信息学奥赛一本通提高组】第二章二分与三分