标签:style blog http color io os ar for sp
题意:
平面上有n条线段,一次给出这n条线段的两个端点的坐标。问怪兽能否从坐标原点逃到无穷远处。(两直线最多有一个交点,且没有三线共交点的情况)
分析:
首先说明一下线段的规范相交:就是交点唯一而且在两条线段的内部。
如果输入中有一条线段uv没有和其他任何一条线段规范相交,那么怪兽一定是可以从u走到v的。
所以我们可以建一个图模型,如果u可以走到v则添加一条边,最后BFS一下看能否从起点走到终点。
再考虑下特殊情况:
题中虽然说三线不会共交点,但貌似不包括三线共端点的情况。
比如这种情况:
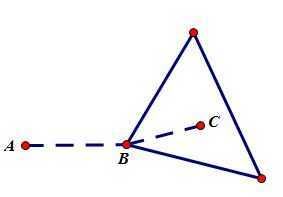
线段AB和BC均不和其他线段规范相交,所以会认为A能走到B,B能走到C。但事实上,这个三角形是封闭的,内部和外部不是连通的。
解决办法就是将线段适当加宽一下(代码中使线段想两侧延伸了1e-6),使其变为规范相交。
还有一种情况就是:
当两个共端点的线段共线的时候,也会出现问题。比如本来应该是封闭的,但因为是根据线段的规范相交来判断是否前进的,所以可能使其变成一条通路。
解决办法就是加框后端点位于其他线段上的点不参与构图。

1 //#define LOCAL 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 #include <iostream> 6 #include <cmath> 7 #include <vector> 8 using namespace std; 9 10 const double eps = 1e-12; 11 int dcmp(double x) 12 { 13 if(fabs(x) < eps) return 0; 14 else return x < 0 ? -1 : 1; 15 } 16 17 struct Point 18 { 19 double x, y; 20 Point(double x=0, double y=0):x(x), y(y) {} 21 }; 22 typedef Point Vector; 23 24 Point operator + (const Point& a, const Point& b) { return Point(a.x+b.x, a.y+b.y); } 25 Point operator - (const Point& a, const Point& b) { return Point(a.x-b.x, a.y-b.y); } 26 Vector operator * (const Vector& a, double p) { return Vector(a.x*p, a.y*p); } 27 Vector operator / (const Vector& a, double p) { return Vector(a.x/p, a.y/p); } 28 bool operator < (const Point& a, const Point& b) 29 { 30 return a.x < b.x || (a.x == b.x && a.y < b.y); 31 } 32 bool operator == (const Point& a, const Point& b) 33 { 34 return a.x == b.x && a.y == b.y; 35 } 36 double Dot(const Vector& a, const Vector& b) { return a.x*b.x + a.y*b.y; } 37 double Cross(const Vector& a, const Vector& b) { return a.x*b.y - a.y*b.x; } 38 double Length(const Vector& a) { return sqrt(Dot(a, a)); } 39 bool SegmentProperIntersection(const Point& a1, const Point& a2, const Point& b1, const Point& b2) 40 { 41 double c1 = Cross(a2-a1, b1-a1), c2 = Cross(a2-a1, b2-a1); 42 double c3 = Cross(b2-b1, a1-b1), c4 = Cross(b2-b1, a2-b1); 43 return dcmp(c1)*dcmp(c2) < 0 && dcmp(c3)*dcmp(c4) < 0; 44 } 45 46 bool OnSegment(const Point& p, const Point& a, const Point& b) 47 { 48 return dcmp(Cross(a-p, b-p)) == 0 && dcmp(Dot(a-p, b-p)) < 0; 49 } 50 51 const int maxn = 200 + 5; 52 int n, V; 53 int G[maxn][maxn], vis[maxn]; 54 Point p1[maxn], p2[maxn]; 55 56 bool OnAnySegment(const Point& p) 57 { 58 for(int i = 0; i < n; ++i) 59 if(OnSegment(p, p1[i], p2[i])) return true; 60 return false; 61 } 62 63 bool IntersectionWithAnySegment(const Point& a, const Point& b) 64 { 65 for(int i = 0; i < n; ++i) 66 if(SegmentProperIntersection(a, b, p1[i], p2[i])) return true; 67 return false; 68 } 69 70 bool dfs(int u) 71 { 72 if(u == 1) return true; 73 vis[u] = 1; 74 for(int v = 0; v < V; ++v) 75 if(G[u][v] && !vis[v] && dfs(v)) return true; 76 return false; 77 } 78 79 bool find_path() 80 { 81 vector<Point> vertices; 82 vertices.push_back(Point(0.0, 0.0)); 83 vertices.push_back(Point(1e5, 1e5)); 84 for(int i = 0; i < n; ++i) 85 { 86 if(!OnAnySegment(p1[i])) vertices.push_back(p1[i]); 87 if(!OnAnySegment(p2[i])) vertices.push_back(p2[i]); 88 } 89 V = vertices.size(); 90 memset(G, 0, sizeof(G)); 91 memset(vis, 0, sizeof(vis)); 92 for(int i = 0; i < V; ++i) 93 for(int j = i+1; j < V; ++j) 94 if(!IntersectionWithAnySegment(vertices[i], vertices[j])) 95 G[i][j] = G[j][i] = 1; 96 return dfs(0); 97 } 98 99 int main(void) 100 { 101 #ifdef LOCAL 102 freopen("2797in.txt", "r", stdin); 103 #endif 104 105 while(scanf("%d", &n) == 1 && n) 106 { 107 double x1, y1, x2, y2; 108 for(int i = 0; i < n; ++i) 109 { 110 scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2); 111 Point a = Point(x1, y1); 112 Point b = Point(x2, y2); 113 double l = Length(a-b); 114 Vector v0 = (a-b) / l * 1e-6; 115 p1[i] = a + v0; 116 p2[i] = b - v0; 117 } 118 if(find_path()) puts("no"); 119 else puts("yes"); 120 } 121 122 return 0; 123 }
LA 2797 (平面直线图PLSG) Monster Trap
标签:style blog http color io os ar for sp
原文地址:http://www.cnblogs.com/AOQNRMGYXLMV/p/4046723.html