B.Sport Mafia

标签：com   col   with   多少   题目   情况   cout   lse   sync   

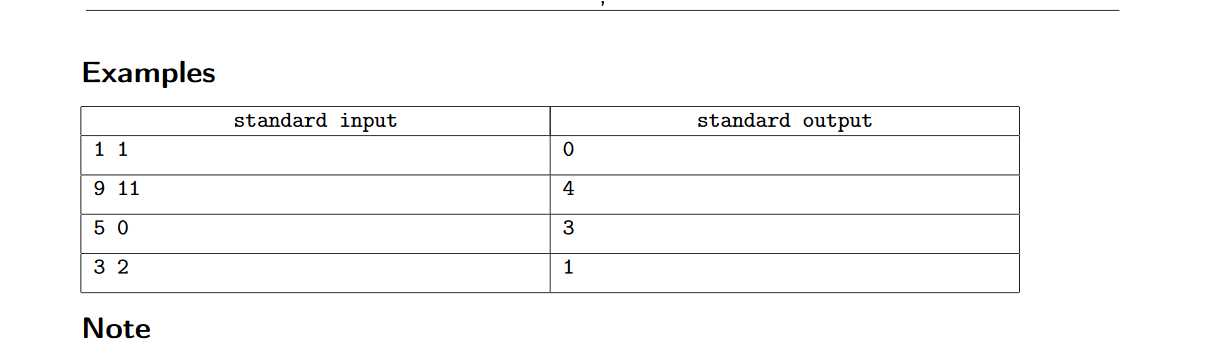
 题意是有两种操作，一种是放蛋糕，一种是吃蛋糕，放蛋糕放的数量是递增的，而吃蛋糕则是固定的每次吃一个

然后题目输入操作步数和最后剩余蛋糕的数量，要求输出吃了多少蛋糕

这道题有两种解法，首先第一种是最容易想到的，就是列方程然后解方程

假设放蛋糕x次，吃蛋糕y次，可以列出:

x + y = n; ①

x(x+1)/2 - y = k;②

将①②联立可得:x^3 + 3x - 2(n+k) = 0

可得x = -3±√9-8(n+k) / 2

然后肯定只有+的情况，所以x= -3+√9-8(n+k) / 2，这样就可以直接算出来放蛋糕的次数x，再拿总次数n减去x就可得出吃蛋糕的次数y

#include<bits/stdc++.h>
using namespace std;

int main(){
  ios::sync_with_stdio(false);
  long long n, k;
  cin >> n >> k;
  cout << n - ( (-3 + (int)sqrt(9+8*(n+k))) / 2 ) << endl;
  return 0;
}

第二种方法是用二分查找，其实也算是暴力穷举，但是毕竟吃蛋糕的数量是限定的，所以可以直接用二分查找在总次数里去枚举，

这算是一个可以学习的点：可以通过二分查找进行降低复杂度的枚举（前提是要枚举的个数有限，且可能结果是依次递增或递减）

然后其它步骤也没什么特别的，就是每次枚举出了一个吃蛋糕的次数，然后放蛋糕的次数自然是总操作次数-吃蛋糕的次数，求出放蛋糕的总和，

拿它减吃的次数，与给定的剩余个数进行对比，若大于它，说明吃的数量少了，要吃更多次，这样就把二分查找的范围向右边缩小。若小于剩余个数，

说明吃得太多了，要减少吃的数量，所以二分查找范围向左边缩小，最后直至找到合适的吃蛋糕数

#include<bits/stdc++.h>
using namespace std;

int main(){
  ios::sync_with_stdio(false);
  long long n, k;
  cin >> n >> k;
  long long l, r;
  l = 0;
  r = n;
  while(l < r){
    long long m = l + (r-l+1)/2;
    if( (n-m)*(n-m+1)/2 - m > k )
      l = m+1;
    else if( (n-m)*(n-m+1)/2 - m < k )
      r = m-1;
    else{
      r = m;
      break;
    }
  }
  cout << r << endl;
  return 0;
}

B.Sport Mafia

标签：com   col   with   多少   题目   情况   cout   lse   sync   

原文地址：https://www.cnblogs.com/ssNiper/p/11216316.html