标签:name 机器 turn 获得 log erro 维度 误差 readline
Logistics回归:实战,有两个特征X0,X1.100个样本,进行Logistics回归
1.导入数据
1 def load_data_set(): 2 """ 3 加载数据集 4 :return:返回两个数组,普通数组 5 data_arr -- 原始数据的特征 6 label_arr -- 原始数据的标签,也就是每条样本对应的类别 7 """ 8 data_arr=[] 9 label_arr=[] 10 f=open(‘TestSet.txt‘,‘r‘) 11 for line in f.readlines(): 12 line_arr=line.strip().split() 13 #为了方便计算,我们将x0的值设为1.0,也就是在每一行的开头添加一个1.0,作为x0 14 data_arr.append([1.0,np.float(line_arr[0]),np.float(line_arr[1])]) 15 label_arr.append(int(line_arr[2])) 16 return data_arr,label_arr
2. Logistics回归梯度上升优化算法
1 def sigmoid(x): 2 return 1.0/(1+np.exp(-x)) 3 4 def grad_ascent(data_arr,class_labels): 5 """ 6 梯度上升法,其实就是因为使用了极大似然估计,这个大家有必要去看推导,只看代码感觉不太够 7 :param data_arr: 传入的就是一个普通的数组,当然你传入一个二维的ndarray也行 8 :param class_labels: class_labels 是类别标签,它是一个 1*100 的行向量。 9 为了便于矩阵计算,需要将该行向量转换为列向量,做法是将原向量转置,再将它赋值给label_mat 10 :return: 11 """ 12 data_mat=np.mat(data_arr) 13 #变成矩阵之后进行转置 14 label_mat=np.mat(class_labels).transpose() 15 #获得数据的样本量和特征维度数 16 m,n=np.shape(data_mat) 17 #学习率 18 alpha=0.001 19 #最大迭代次数 20 max_cycles=500 21 # 生成一个长度和特征数相同的矩阵,此处n为3 -> [[1],[1],[1]] 22 # weights 代表回归系数, 此处的 ones((n,1)) 创建一个长度和特征数相同的矩阵,其中的数全部都是 1 23 weights=np.ones((n,1)) 24 for k in range(max_cycles): 25 h=sigmoid(data_mat*weights) 26 error=label_mat-h 27 weights=weights+alpha*data_mat.transpose()*error 28 return weights
3. 画出决策边界,即画出数据集合Logistics回归最佳拟合直接的函数
1 def plot_best_fit(weights): 2 """ 3 可视化 4 :param weights: 5 :return: 6 """ 7 import matplotlib.pyplot as plt 8 data_mat, label_mat = load_data_set() 9 data_arr = np.array(data_mat) 10 n = np.shape(data_mat)[0] 11 x_cord1 = [] 12 y_cord1 = [] 13 x_cord2 = [] 14 y_cord2 = [] 15 for i in range(n): 16 if int(label_mat[i]) == 1: 17 x_cord1.append(data_arr[i, 1]) 18 y_cord1.append(data_arr[i, 2]) 19 else: 20 x_cord2.append(data_arr[i, 1]) 21 y_cord2.append(data_arr[i, 2]) 22 fig = plt.figure() 23 ax = fig.add_subplot(111) 24 ax.scatter(x_cord1, y_cord1, s=30, color=‘k‘, marker=‘^‘) 25 ax.scatter(x_cord2, y_cord2, s=30, color=‘red‘, marker=‘s‘) 26 x = np.arange(-3.0, 3.0, 0.1) 27 y = (-weights[0] - weights[1] * x) / weights[2] 28 """ 29 y的由来,卧槽,是不是没看懂? 30 首先理论上是这个样子的。 31 dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) 32 w0*x0+w1*x1+w2*x2=f(x) 33 x0最开始就设置为1叻, x2就是我们画图的y值,而f(x)被我们磨合误差给算到w0,w1,w2身上去了 34 所以: w0+w1*x+w2*y=0 => y = (-w0-w1*x)/w2 35 """ 36 ax.plot(x, y) 37 plt.xlabel(‘x1‘) 38 plt.ylabel(‘y1‘) 39 plt.show()
4. 测试数据,画图
1 def test(): 2 """ 3 这个函数只要就是对上面的几个算法的测试,这样就不用每次都在power shell 里面操作,不然麻烦死了 4 :return: 5 """ 6 data_arr, class_labels = load_data_set() 7 # 注意,这里的grad_ascent返回的是一个 matrix, 所以要使用getA方法变成ndarray类型 8 weights = grad_ascent(data_arr, class_labels).getA() 9 # weights = stoc_grad_ascent0(np.array(data_arr), class_labels) 10 #weights = stoc_grad_ascent1(np.array(data_arr), class_labels) 11 plot_best_fit(weights) 12 13 if __name__ == ‘__main__‘: 14 test()
5. 结果如下
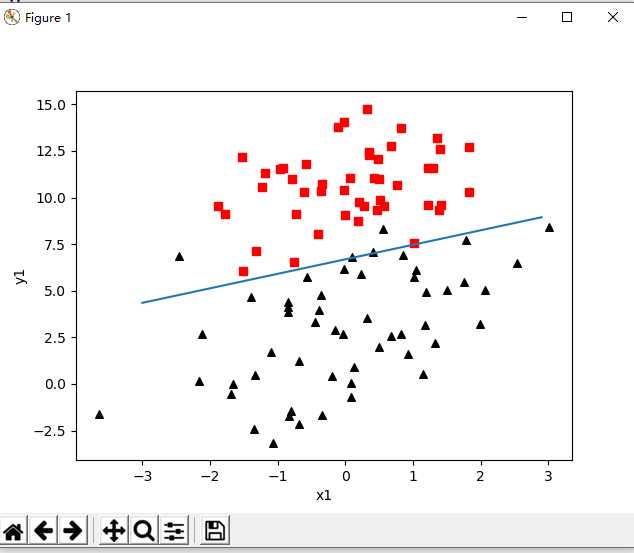
另外,还有
真实训练数据和测试数据-------从疝气病症预测病马的死亡率------
如何预测的代码也附加~
github实现地址:https://github.com/CynthiaWendy/Machine-Learning-in-Action-Logistics
标签:name 机器 turn 获得 log erro 维度 误差 readline
原文地址:https://www.cnblogs.com/CynthiaWendy/p/11217272.html