标签:span mamicode 定义 def not 调用 有根树 记录 http
题目描述:
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
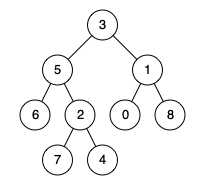
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
说明:
思路分析:
这道题一开始想得比较复杂,对于p、q两个结点,都分别用两个双向队列去树中从根往下查找这两个结点,并将其对应的路径存在队列中。最后再从队首开始做出队操作,知道两个队列的队首不相等,那么最后一个相等的结点即为最近的公共祖先。这个思路可以,但在实现的过程中其实还是比较繁琐的,在记录路径的过程中其实还涉及到了回溯的操作。
换一个思路,与树相关的问题,其实用递归来解决会更简单。这里我的问题实际上是对于一个问题,没有首先做分析思考,最直接的去想做法。其实分析起来,包括三类情况,p、q分别位于当前根结点的左右子树中,那么当前的根结点即为最近公共祖先;p、q都位于左子树中,那么当前的根结点就换为左子树,递归调用这个找公共祖先的函数;右子树的情况是类似的。所以实际只需要写两个函数,一个函数是判断结点是否在当前树中,一个是递归的找最近公共祖先。那么找公共祖先的这个函数的递归停止条件就是当前的根为p或q任意结点,或是p和q分别在当前根结点的左右子树中。
代码:
1 /** 2 * Definition for a binary tree node. 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {} 8 * }; 9 */ 10 class Solution { 11 public: 12 bool in_tree(TreeNode* root, TreeNode* cur) 13 { 14 if(root == NULL) 15 return false; 16 if(root == cur) 17 return true; 18 else if(in_tree(root->left, cur) || in_tree(root->right, cur)) 19 return true; 20 else 21 return false; 22 } 23 TreeNode* lowestCommonAncestorCore(TreeNode* root, TreeNode* p, TreeNode* q) 24 { 25 if(p == root || q == root) 26 return root; 27 if(in_tree(root->left, p) && in_tree(root->right, q)) 28 return root; 29 else if(in_tree(root->left, q) && in_tree(root->right, p)) 30 return root; 31 else if(in_tree(root->left, p) && in_tree(root->left, q)) 32 return lowestCommonAncestorCore(root->left, p, q); 33 else 34 return lowestCommonAncestorCore(root->right, p, q); 35 } 36 TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { 37 if(root == NULL || p == NULL || q == NULL) 38 return root; 39 40 TreeNode* res = lowestCommonAncestorCore(root, p, q); 41 return res; 42 } 43 };
标签:span mamicode 定义 def not 调用 有根树 记录 http
原文地址:https://www.cnblogs.com/LJ-LJ/p/11217873.html