标签:割边 style 没有 string tarjan int 两种方法 return 存在
题目描述:
给定无向图G,包含n个点m条边(不保证连通),求有序三元组(s,c,f)个数要求满足 s, c, f 都是图中的点,且存在一条从s到c的路径和一条从c到f的路径,使得两条路径没有公共点(除c外)。
在这里我们引进圆方树的概念。
但首先我们要了解一下点双和边双。
在无向图中:
点双:极大的连通子图,使得删掉这个子图中的任何一个点,这个子图仍然连通。
也就是说,在这个极大的连通子图中没有割点。
也就是说,在这个极大的连通子图中两个不同节点可以通过两条没有公共点的路径互相到达,但是排除起点和终点。
所以,u——v这也是个点双。
边双:极大的连通子图,使得删掉这个子图中的任何一条边,这个子图仍然连通。
也就是说,在这个极大的连通子图中没有割边。
也就是说,在这个极大的连通子图中两个不同节点可以通过两条没有公共边的路径互相到达。
那么我们考虑如何求点双,边双:
边双:很简单,我们断开所有的割边,剩下的每个连通子图就是一个边双强连通分量。
代码:
void tarjan(int u, int pre) { stk[++top] = u; dfn[u] = low[u] = ++idx; for(int e = adj[u], v; e; e = nxt[e]) { if(!dfn[v = go[e]]) { tarjan(v, u); low[u] = min(low[u], low[v]); if(low[v] > dfn[u]) { is_bridge[e] = is_bridge[e^1] = 1; cnt++; do bel[stk[top]] = cnt; while(stk[top--] != v); } } else if(v != pre) low[u] = min(low[u], dfn[v]); } }
点双:那么是否删去所有割点,剩 下的连通块都是点双呢?
…不是的!一个点可能属于不同的点双!
比如 a——b——c ,b属于两个点双集合。
求点双有两种方法:
一种求点双的?法是把边压入栈中,当发现low[v] >= dfn[u] 时,把边(u,v)及它以上的所有边从栈中弹出,这些边所涉及的点共同形成?个点双(显然包括u)。
另?种方法是像别的Tarjan算法?样把点压入栈中,当发现 low[v] >= dfn[u]时,把v及v以上的点从栈中弹出,再加上u,共同形成?个点双。
我个人喜欢后一种……
有几个细节需要注意:
1.弹元素的时候,我们不能弹u,我们弹到v,因为到u的所有元素可能构成别的点双。
比如这样一个图:
a - u , u - b , b - a , u - v , v - x , x - u 。
这样的图,栈是这样的:(从上往下):x,v,b,u,a.
那么我们从v回溯到u的时候,第一次弹元素,u应该和v,x构成一个点双。但是v和u之间还有一个b,我们显然不能将b放到这个点双集合中(就因为v和u之间可能还有其他元素),所以我们只能弹到v。
2.虽然弹到v,u也要算在这个点双集合中。
因为既然到v才满足>=关系,说明下面一定有一个点连到u这里,u也一定包含在这个点双集合中,不能忘了!
代码:
void tarjan(int u,int fa) { dfn[u]=low[u]=++tot; st[++top]=u; for(int i=head[u];i;i=nxt[i]) { int v=to[i]; if(!dfn[v]) { tarjan(v,u); low[u]=min(low[u],low[v]); if(low[v]>=dfn[u]) { num++; do { ... top--; } while(st[top]!=v) } } else if(v!=fa) low[u]=min(low[u],dfn[v]); } }
先在我们可以引进圆方树的概念了:
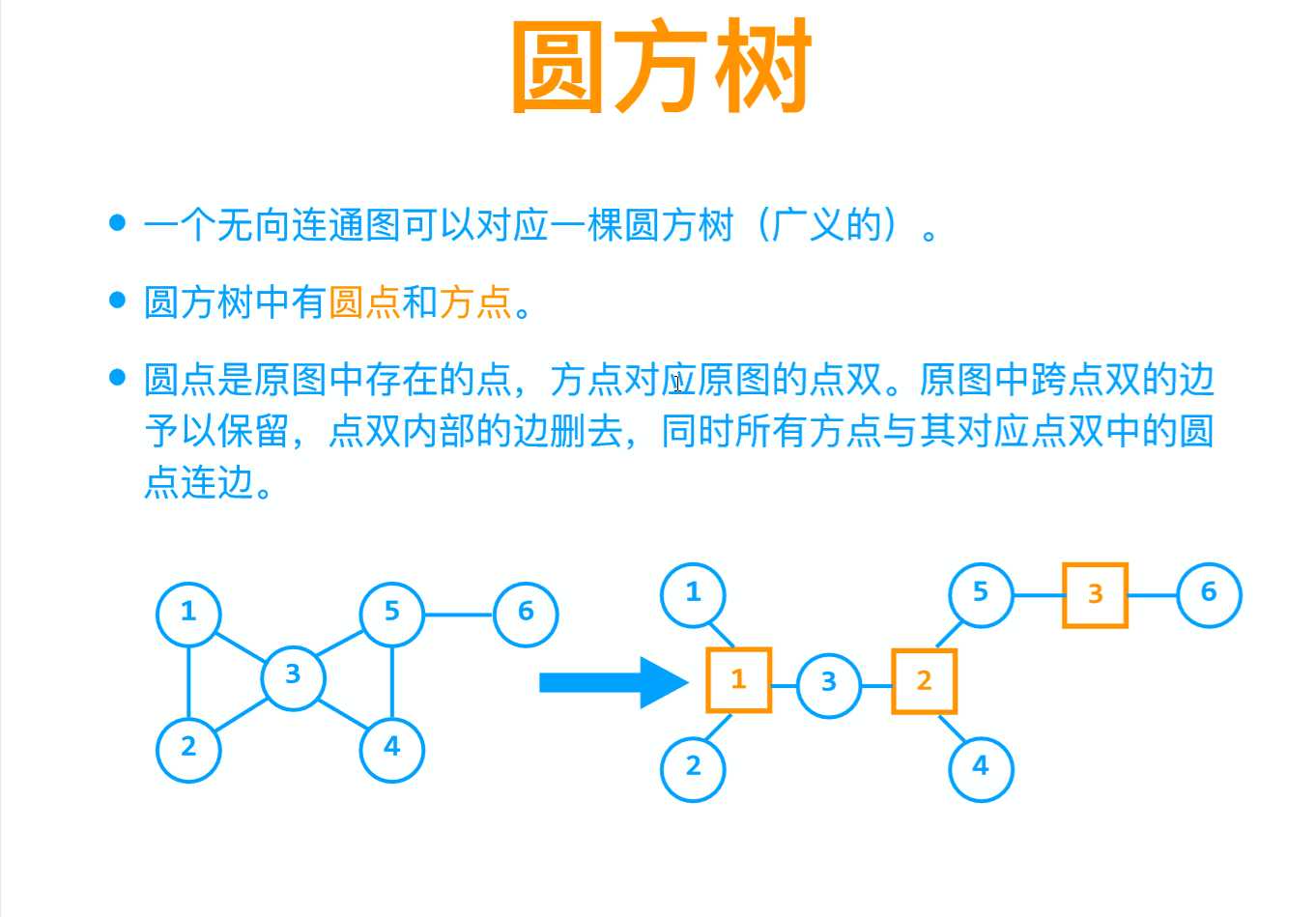
那么圆方树怎么建呢?
其实很容易,只要对于每一个割点u的孩子v,元素弹到v(包含v),他们和u共同构成一个点双强连通分量(上文已经解释过),那么我们把这些点和u连到一个方点上就可以了。
知道了点双边双,会建圆方树,我们来看看这道题:
我们首先考虑 O(n2) 的做法,就是枚举两个端点,这两个端点在我们的圆方树上之间有且只有一条路径。那么这条路径上既园点又有方点。所有方点所对应的原点都可以做为我们的中转点,于是每一个方点的权值我们都记录这个点所连的圆点个数,我们希望把这些方点的权值加起来求路径长。但是我们发现有重复,相邻的方点都包含他们之间的圆点,所以我们把圆点的权值设为-1,这样就保证每个圆点只被统计一遍。
其实我们的问题已经转化成:统计树上所有路径上的点权权值和之和了,其中圆点可以作为起点和终点,方点不可以。
枚举路径显然不优,所以我们考虑计算每个点的贡献。
我们设sum为这个圆方树上圆点的个数(注意是圆点的个数!因为方点没有实际意义,圆点才是真正可以选的点,方点只是方便计算答案而设计的)
对于一个方点,它只能作为中转点,那么经过这个点的路径有(sum-sz[u])*sz[u]+sz[v]*(sum-sz[v]);(v是u的儿子)不减1是因为方点不是一个真正的点。
对于一个圆点,作为中转点时,经过这个点的路径有:(sum-sz[u])*(sz[u]-1)+sz[v]*(sum-sz[v]-1);v是u的儿子)不减1是因为圆点是一个真正的点。
这样复杂度就是O(n)了!
代码:
#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> using namespace std; #define maxn 400000 #define ll long long int head[maxn],to[maxn],nxt[maxn],w[maxn],st[maxn]; int H[maxn],T[maxn],N[maxn],dfn[maxn],low[maxn],sz[maxn]; int cnt,CNT,n,m,num,tot,top,sum; ll ans; void add(int a,int b) { to[++cnt]=b; nxt[cnt]=head[a]; head[a]=cnt; } void ADD(int a,int b) { T[++CNT]=b; N[CNT]=H[a]; H[a]=CNT; } void Tarjan(int u,int fa) { dfn[u]=low[u]=++tot; st[++top]=u; for(int i=head[u]; i; i=nxt[i]) { int v=to[i]; if(!dfn[v]) { Tarjan(v,u); low[u]=min(low[u],low[v]); if(low[v]>=dfn[u]) { int am=0; ++num; while(st[top]!=v) { am++; ADD(st[top],n+num); ADD(n+num,st[top]); top--; } am++; ADD(v,n+num); ADD(n+num,v); top--; am++; ADD(u,n+num); ADD(n+num,u); w[n+num]=am; } } else if(v!=fa) low[u]=min(low[u],dfn[v]); } } void dfs(int u,int fa) { if(w[u]==-1) sz[u]=1; for(int i=H[u]; i; i=N[i]) { int v=T[i]; if(v==fa) continue; dfs(v,u); sz[u]+=sz[v]; } } void dp(int u,int fa) { if(w[u]==-1) ans+=1ll*(sum-1)*w[u]*2; ans+=1ll*(sum-sz[u])*w[u]*(sz[u]-(w[u]==-1)); for(int i=H[u]; i; i=N[i]) { int v=T[i]; if(v==fa) continue; ans+=1ll*sz[v]*(sum-(w[u]==-1)-sz[v])*w[u]; dp(v,u); } } void solve(int u) { dfs(u,0); sum=sz[u]; dp(u,0); } int main() { scanf("%d%d",&n,&m); for(int i=1; i<=n; i++) w[i]=-1; for(int i=1; i<=m; i++) { int a,b; scanf("%d%d",&a,&b); add(a,b); add(b,a); } for(int i=1; i<=n; i++) { if(!dfn[i]) { Tarjan(i,0); solve(i); } } printf("%lld\n",ans); return 0; }
以及——别忘开long long!加油呀!
标签:割边 style 没有 string tarjan int 两种方法 return 存在
原文地址:https://www.cnblogs.com/popo-black-cat/p/11219120.html