标签：方便 block 密度 auto 函数 随机梯度 bat 线性 解决
1 线性回归的模型
线性回归的模型十分的简单，就是对回归问题中每一个特征X乘以一个系数，使其拟合到输出Y，线性回归模型就是找到这样一组系数。
线性回归的模型如下：
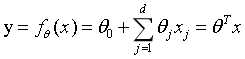
其中x是数据的特征，是一个d维的列向量，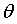
是权重系数，也是一个d维的列向量，y是模型的输出
2 线性回归的损失函数
在做回归问题的时候，模型的预测输出值和真实值总是存在一个误差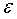
，误差
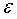满足均值为0，标准差为
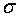的高斯分布，则线性归回的模型变为
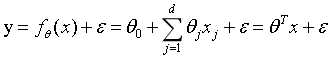
其中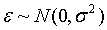
。
由于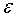
满足高斯分布，则其概率密度函数为：
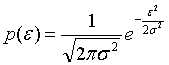
将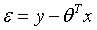
带入上式密度函数中，得到：
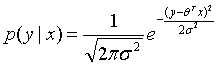
上式即为似然函数，为了使模型更好的拟合数据集，需要最大化似然函数：
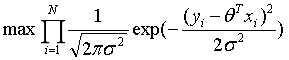
其中N使数据集的个数。
为了计算方便，对上式取对数：
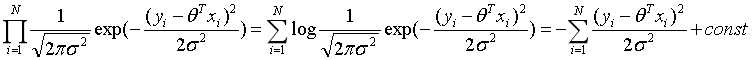
其中const是一个常数，则最大化上式可等价于下式：
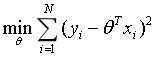
则定义线性回归的损失函数为：
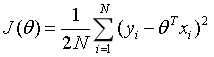
3 优化线性回归模型
由上一节得到线性归回的损失函数为：
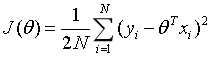
需要优化的问题是：找到一组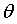
，使上式的损失函数最小，即对损失函数求导：
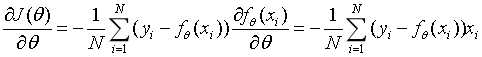则参数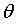 
可通过迭代求解：
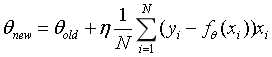
其中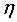
为学习率。
上式的迭代算法是批量梯度下降算法(BGD)，每更新一次，需要计算所有样本上的梯度的平均值。
下面是随机梯度下降(SGD)，每更新一次，只是从样本数据中随机挑选一个样本来计算梯度值：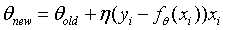
最后一个为小批量随机梯度下降(Mini-Batch GD)，每更新一次，从所有样本中随机挑选一批样本来计算这一批的梯度的平均值：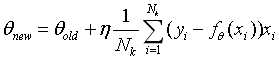
其中Nk为小批量的个数。
4 张量视角
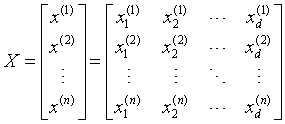
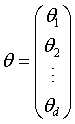
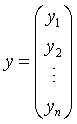
其中X为样本，n为样本的个数，d为样本的特征个数，即每一行为一个样本。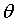
是模型的参数，是一个d维的列向量。y是样本的标签，是一个n维的列向量。
则，线性回归模型的矩阵形式为：
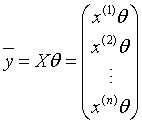
线性回归的损失函数的矩阵形式为：
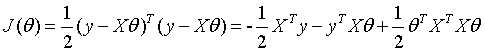
上式对向量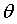
求梯度，即矩阵对向量求梯度，需要以下矩阵对向量的知识才能得出：
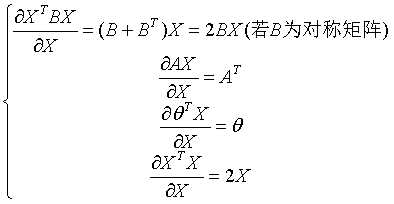
则可求出J对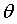
的梯度为：
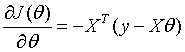
让上式子等于零，可求出最优的参数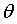
：
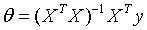
5 线性回归模型的正则化
线性回归模型的正则化可解决两个问题：
1 可以解决模型的过拟合问题
2 若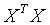
奇异，即不可逆，则上节用最小二乘法就求不出解，加入正则化项则可解决这一问题
加入L2正则化项的损失函数：
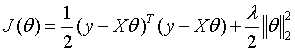
求梯度：
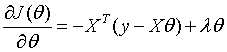
求解：
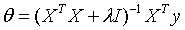
标签：方便 block 密度 auto 函数 随机梯度 bat 线性 解决
原文地址：https://www.cnblogs.com/swenwen/p/11220539.html
