标签:节点 就是 def win start wing lis bec nat
We distribute some number of candies, to a row of n = num_people people in the following way:
We then give 1 candy to the first person, 2 candies to the second person, and so on until we give n candies to the last person.
Then, we go back to the start of the row, giving n + 1 candies to the first person, n + 2 candies to the second person, and so on until we give 2 * n candies to the last person.
This process repeats (with us giving one more candy each time, and moving to the start of the row after we reach the end) until we run out of candies. The last person will receive all of our remaining candies (not necessarily one more than the previous gift).
Return an array (of length num_people and sum candies) that represents the final distribution of candies.
Example 1:
Input: candies = 7, num_people = 4 Output: [1,2,3,1] Explanation: On the first turn, ans[0] += 1, and the array is [1,0,0,0]. On the second turn, ans[1] += 2, and the array is [1,2,0,0]. On the third turn, ans[2] += 3, and the array is [1,2,3,0]. On the fourth turn, ans[3] += 1 (because there is only one candy left), and the final array is [1,2,3,1].
Example 2:
Input: candies = 10, num_people = 3 Output: [5,2,3] Explanation: On the first turn, ans[0] += 1, and the array is [1,0,0]. On the second turn, ans[1] += 2, and the array is [1,2,0]. On the third turn, ans[2] += 3, and the array is [1,2,3]. On the fourth turn, ans[0] += 4, and the final array is [5,2,3].
Constraints:
题目大意:给n个人分糖果,从0到n-1依次发,发完如果还剩下就循环再发。
思路:暴力模拟。

class Solution { public int[] distributeCandies(int candies, int num_people) { int[] res = new int[num_people]; int x = 1, ind = 0; while( candies >= x ) { res[ind] += x; candies -= x; x ++; ind = (ind+1)%num_people; } if( candies>=0 ) res[ind] += candies; return res; } }
In an infinite binary tree where every node has two children, the nodes are labelled in row order.
In the odd numbered rows (ie., the first, third, fifth,...), the labelling is left to right, while in the even numbered rows (second, fourth, sixth,...), the labelling is right to left.
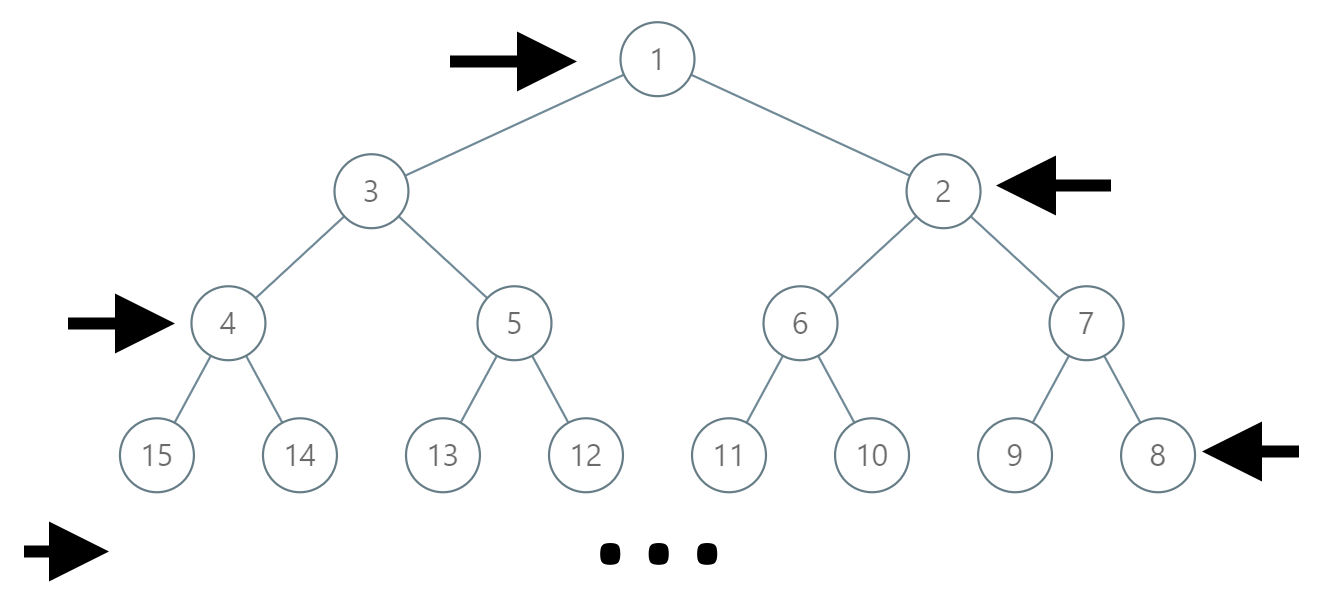
Given the label of a node in this tree, return the labels in the path from the root of the tree to the node with that label.
Example 1:
Input: label = 14 Output: [1,3,4,14]
Example 2:
Input: label = 26 Output: [1,2,6,10,26]
Constraints:
1 <= label <= 10^6题目大意:给你树上的一个节点n,求从n到根节点1的路径。但是这个树的节点是由逐行 依次按 “之” 字形进行标记。也就是:
在奇数行(即,第一行、第三行、第五行……)中,按从左到右的顺序进行标记;
而偶数行(即,第二行、第四行、第六行……)中,按从右到左的顺序进行标记。
思路:虽然节点排列变了,但是其所在的层数是不变的,根据层数,往下递推,当层数是奇数的时候,将左右子树倒过来就好

class Solution { private int getLevel(int n) { int cnt = 0; int level = 0; for(level=0; ; level++) { cnt += Math.pow(2, level); if( cnt >= n ) return level; } } public List<Integer> pathInZigZagTree(int label) { List<Integer> list = new ArrayList<>(); int level = getLevel(label); int cnt = 0; while( label > 0 ) { int res = label; if( cnt%2==1 && res != 1 ) { int low = (int) Math.pow(2, level); int high = (int) Math.pow(2, level+1)-1; res = low+high-res; } list.add(res); label /= 2; cnt ++; level --; } Collections.reverse(list); return list; } }
标签:节点 就是 def win start wing lis bec nat
原文地址:https://www.cnblogs.com/Asimple/p/11220824.html