标签:路径 ref dia 弧度 计算 色值 重要 context 数学
经过 canvas 教程(二) 绘制直线 我们知道了 canvas 的直线是怎么绘制的
而本次是给大家带来曲线相关的绘制
在 canvas 中我们可以使用 arc 方法画一个圆
context.beginPath();
context.arc(x, y, r, startRadian, endRadian, antclockwise);
context.closePath();我们是第一次用到 beginPath 和 closePath 这两个方法,首先这两个方法故名思意就是开始路径和结束路径,一般都是配合使用的。
对于 arc 的方法的参数,x 和 y 代表的是圆心的坐标,r 是指圆的半径,startRadian 和 endRadian 是指开始的角度和结束的角度
注意:这里是以弧度为单位的!1π 等于 180 度,所以我们这里写的时候一般是写成 度数*Math.PI/180,方便我们一眼看出度数是多少
而 antclockwise 是指是否是逆时针绘制,默认是 false
有朋友会说了,我试了一下,写了这三句没有效果啊,怎么回事?没有效果是肯定的,因为这三句仅仅只是描述了一个路径!并没有绘制!所以我们可以用上绘制直线中使用的“描边”stroke 或者“填充”fill
描边三角形:
context.beginPath();
context.arc(x, y, r, startRadian, endRadian, antclockwise);
context.closePath();
context.strokeStyle = '颜色值';
context.stroke();
//描边 填充fill 同理 就不写了弧线是圆的一部分,那么如何绘制一个弧度呢,有朋友就发现了我们刚才的 arc 也有一个弧度,
只是两个弧度之间的点有连接的一条直线,那么我去掉直线是不是就是弧线了呢?宾果!就是这样,只要你去掉 closePath 就会发现你画了一条弧线了 2333
好了那么 canvas 其实还有一个画弧线的方法 arcTo(x1,y1,x2,y2,radius);
我们要通过 arcTo 画一条弧线,需要提供三个点的坐标,开始点一般是通过 moveTo 和 lineTo 提供
x1 和 y1 是控制点,x2 和 y2 是结束点,radius 则是圆弧的半径
arcTo()方法将利用当前端点、端点 1(x1,y1)和端点 2(x2,y2)这三个点所形成的夹角
然后绘制一段与夹角的两边相切并且半径为 radius 的圆上的弧线
弧线的起点就是当前端点所在边与圆的切点
弧线的终点就是端点 2(x2,y2)所在边与圆的切点,并且绘制的弧线是两个切点之间长度最短的那个圆弧。
如果当前端点不是弧线起点,arcTo()方法还将添加一条当前端点到弧线起点的直线线段。我画一个图:

咳咳,别介意画工,大概就是这样的,开始点是我们的当前的点就是使用 arcTo 之前的点
下面我写两段代码演示一下起点一致和起点不一致的情况
context.moveTo(50, 50);
context.lineTo(150, 50);
ctx.arcTo(200,50, 200,100, 50);
ctx.stroke(); context.moveTo(50, 50);
ctx.arcTo(200,50, 200,100, 50);
ctx.stroke();是不是发现结果是一样的!
其中区别就细细品味吧,数学知识可以补一补
百度百科:贝塞尔曲线(Bézier curve),又称贝兹曲线或贝济埃曲线,是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线,贝兹曲线由线段与节点组成,节点是可拖动的支点,线段像可伸缩的皮筋,我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。贝塞尔曲线是计算机图形学中相当重要的参数曲线,在一些比较成熟的位图软件中也有贝塞尔曲线工具,如PhotoShop等。更多的就大家自行搜索吧,由于一次贝塞尔曲线就是直线,这里就不讲了,我们直接讲 canvas 如何绘制二次贝塞尔曲线
cnavas 提供了一个方法 quadraticCurveTo(x1,y1,x2,y2), 其中参数 x1 和 y1 是控制点,x2 和 y2 是结束点
起始点是调用方法之前的点
动图我不会画,但是我之前网上找到一个:
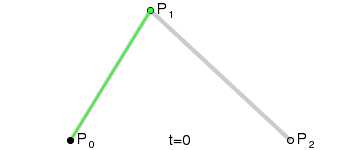
context.strokeStyle = 'red';
context.beginPath();
context.moveTo(0, 150);
context.quadraticCurveTo(75, 50, 200, 100);
context.stroke();
context.strokeStyle = 'green';
context.beginPath();
context.moveTo(75, 50);
context.lineTo(0, 150);
context.moveTo(75, 50);
context.lineTo(200, 100);
context.stroke();代码效果:

三次贝塞尔曲线的方法则是 bezierCurveTo(x1,y1,x2,y2,x3,y3)
其中参数 x1、y1,x2、y2 是控制点,x3 和 y3 是结束点
就是提供多一个控制点!
画图原理是这样:

这个例子就不写了,大家照着二次贝塞尔曲线的例子,练习一下!
本次讲了:绘制圆形、绘制弧线、二次贝赛尔曲线、三次贝赛尔曲线,大家学会了多少呢?
好了,本次的教程就到这里结束了,下次将为大家带来线条和文本的操作
标签:路径 ref dia 弧度 计算 色值 重要 context 数学
原文地址:https://www.cnblogs.com/cnyball/p/11225131.html