P4136 谁能赢呢？ 脑子

标签：using   pause   ==   ace   ipa   cpp   math   中间   line   

思路：脑子（教练说是博弈论？）

提交：1次

题解：

结论：若\(n\)为奇数后手胜，若\(n\)为偶数先手胜。

大致证明：

我们发现，若我们把棋盘黑白染色并设左上角为黑色，那么显然有：若\(n\)为奇数，黑色格子比白色多一；若\(n\)为偶数，黑色格子与白色的相等。

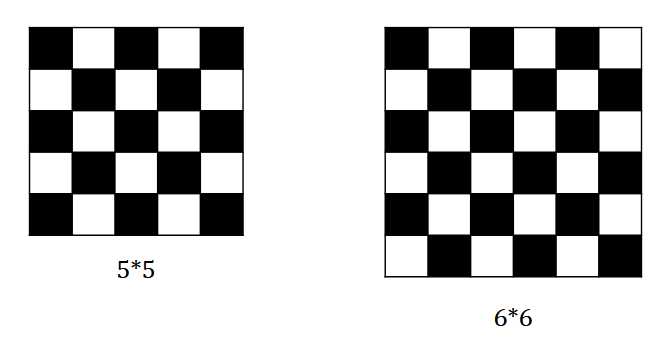
然后很显然，如果他们能够把所有格子都走到或少走\(2*x\)个格子（即不改变奇偶性），那么上面的结论是成立的。
若最后有奇数个格子没有走到，那么其实我们可以在中间改变最终的状态。比如只剩了一个格子没有走，那么最后输的人完全可以在经过那一个格子时杀掉对方。
即若有奇数个格子剩余，不是最优策略。
所以不可能有奇数个格子是未被经过的。
所以我们证完啦\(QwQ\)

代码

冗长版

#include<cstdio>
#include<iostream>
#define ull unsigned long long
#define ll long long
#define R register int
using namespace std;
#define pause (for(R i=1;i<=10000000000;++i))
#define In freopen("NOIPAK++.in","r",stdin)
#define Out freopen("out.out","w",stdout)
namespace Fread {
static char B[1<<15],*S=B,*D=B;
#ifndef JACK
#define getchar() (S==D&&(D=(S=B)+fread(B,1,1<<15,stdin),S==D)?EOF:*S++)
#endif
inline int g() {
    R ret=0,fix=1; register char ch; while(!isdigit(ch=getchar())) fix=ch=='-'?-1:fix;
    if(ch==EOF) return EOF; do ret=ret*10+(ch^48); while(isdigit(ch=getchar())); return ret*fix;
} inline bool isempty(const char& ch) {return (ch<=36||ch>=127);}
inline void gs(char* s) {
    register char ch; while(isempty(ch=getchar()));
    do *s++=ch; while(!isempty(ch=getchar()));
}
} using Fread::g; using Fread::gs;

namespace Luitaryi {
inline void main() { R x;
    while(x=g(),x!=0) x&1?puts("Bob"):puts("Alice");
}
}
signed main() {
    Luitaryi::main(); return 0;
}

极简版

main() {int n; while(__builtin_scanf("%d",&n),n!=0) __builtin_printf(n&1?"Bob\n":"Alice\n");}

2019.07.22

P4136 谁能赢呢？ 脑子

标签：using   pause   ==   ace   ipa   cpp   math   中间   line   

原文地址：https://www.cnblogs.com/Jackpei/p/11228957.html