标签:编号 删除 include idt isp ret print splay return
前言部分
splay是个什么东西呢?
它就是个平衡树,支持以下操作

这些操作还可以用treap,替罪羊树,红黑树,multiset balabala(好像混进去什么奇怪的东西)
这里就只说一下splay(其他的窝不会)(splay窝也不会 )
)
先来几个变量和一些辅助函数:
root:当前平衡树的根是那个节点
sz:整个平衡树的大小
ch[x][0]:x的左儿子的编号
ch[x][1]:x的右儿子的编号
size[x]:x和它的子树的大小
cnt[x]:编号为x的点的权值出现了几次
par[x]:x的父亲的编号
key[x]:编号为x的点的权值
get(x):查询x是它父亲的左儿子还是右儿子(左儿子返回0,右儿子返回1)
pushup(x):统计x的size和cnt
clear(x):将x的ch,size,cnt,key清0(删除用)
代码:
void pushup(int x) { size[x]=size[ch[x][0]]+size[ch[x][1]]+cnt[x];//左子树+右子树+自身的cnt return ; } void clear(int x) { size[x]=0;ch[x][0]=0;ch[x][1]=0;key[x]=0;cnt[x]=0;par[x]=0; return ;//全部清0就好辣 } bool get(int x) { return ((ch[par[x]][1]==x)?1:0);//如果x是自己父亲的右儿子,就返回1,否则返回0 }
正文开始
一.一些基础操作
说了辣么多,还没有介绍平衡树到底是个什么东西
不过不着急,我们先来看看二叉搜索树
二叉搜索树有一个神奇的性质:所有比当前节点x权值小的节点,都在x的左子树里面,权值比x大的点都在x的右子树里
有了这个神奇的性质,在一般情况下树高就是log级别的,查询的复杂度也就降到了log级别,这很好对不对?
但是duliu出题人总是会种出一些歪七扭八的二叉搜索树(节点里面的数是权值)
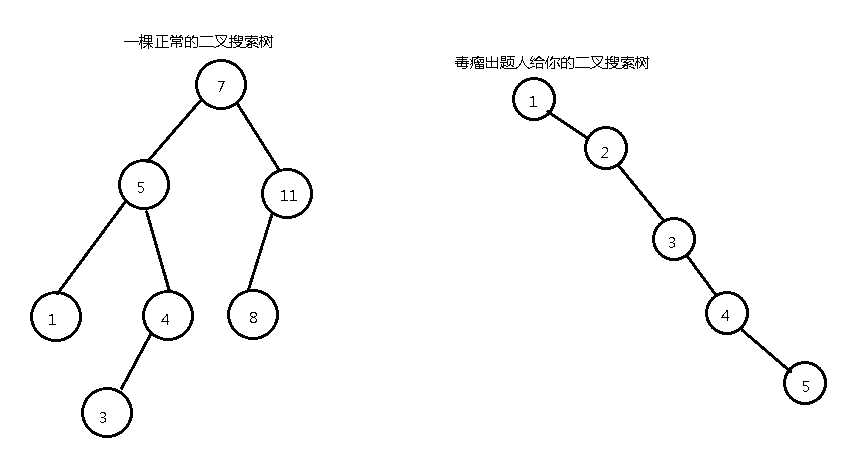
对于第二种毒瘤的二叉搜索树,复杂度就退化成了O(n),这不优美。我们想让它成长,让它学会自己平衡。于是,它成长成了平衡树。
splay如何做到自己平衡?
我们看这个丑陋的树:
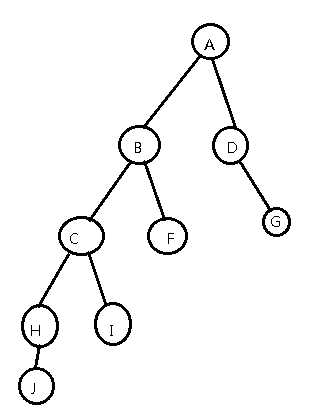
转一转(右旋)
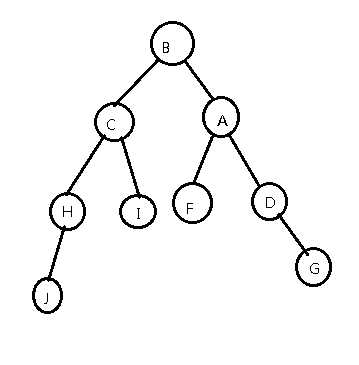
我们发现,B原本的右儿子成了A的左儿子,B现在的右儿子是A,其余不变
为什么这样转?
我们把B转成了根,那么B就没有父亲了,但是多了A这个右儿子,需要处理成二叉。同时A失去了左儿子,并且A发现B还有一个原来的右儿子F,F比A小,于是A就让F当自己的左儿子
如果我们把A左旋(然后这个树就更不平衡了ρωρ)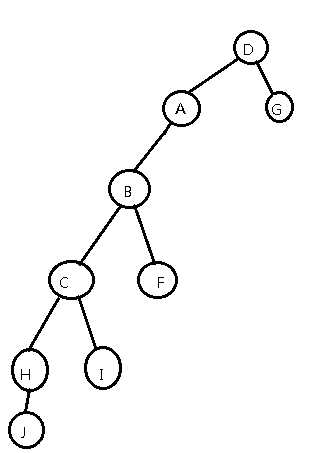
我们发现A没有右儿子了,D的左儿子变成了A
旋转的方式和右旋差不多,这里是让D的左儿子认A当爹,让A认D当爹。
不过可惜D并没有左儿子,于是A转完了也就没有右儿子辣。
我们可以总结出旋转的规律:
现在我们要把x转到根的位置(不管现在x在哪)
我们用k表示x是它父亲的左儿子还是右儿子(0是左儿子,1是右儿子),y是x的儿子
就让y的k方向的儿子变成x的与k相反方向的儿子,y认x为爹,同时让y的父亲在y这个方向上的儿子替换成x
说人话版本:
y=par[x],z=par[y],k=get(x),e=get(y)
ch[y][k]=ch[x][k^1]
par[ch[y][k]]=y
par[y]=x
ch[x][k^1]=y
par[x]=z
ch[z][e]=x
代码版本:
void rotate(int x) { int y=par[x],z=par[y],k=get(x),e=get(y); ch[y][k]=ch[x][k^1];par[ch[y][k]]=y; par[y]=x;ch[x][k^1]=y; par[x]=z; if(z) ch[z][e]=x; pushup(y);pushup(x);//记得pushup回去(统计信息) }
当然只旋转一次是肯定不够的,所以我们再来一个splay函数。
splay(x)就是把x旋转到根(当然也可以再带一个参数,让x旋转到那个参数去)
定义fa,让fa一直等于当前x的父亲,一直旋转x,直到x的父亲是0(x是根节点)
注意:如果x,x的父亲,x的爷爷在同一条线上,就先转x的父亲
void splay(int x) { for(int fa;fa=par[x];rotate(x)) if(par[fa]) rotate((get(x)==get(fa))?fa:x); root=x; }
好像有什么不对的???

貌似这些操作一个都没有实现ρωρ
那就开始讲这些操作好了
二.平衡树支持的操作
1.插入X
如果当前平衡树里面没有元素,就直接sz++,root=sz
如果当前点的权值>x,就到左子树找x,反之则到右子树找,直到找到x,然后更新cnt,size,顺便再splay一下
如果找到最后都没有x,就说明x先前不在平衡树里,就新建一个节点,其权值为x,维护cnt,size

void insert(int x) { if(root==0) { sz++; key[sz]=x; root=sz; cnt[sz]=1;size[sz]=1; par[sz]=ch[sz][0]=ch[sz][1]=0; return;//这里由于只有一个节点,就不需要splay了 } int now=root,fa=0; while(1) { if(key[now]==x) { cnt[now]++; pushup(now);//先更新now,再更新fa pushup(fa); splay(now); //为了以后方便,我们要把当前点splay到根 return ; } fa=now; now=ch[now][key[now]<x];//第二维表示的是如果key[now]<x,就返回1,否则是0 if(now==0)//最终没有找着(不存在的节点默认值是0) { sz++; size[sz]=1;cnt[sz]=1; root=sz; key[sz]=x; ch[fa][key[fa]<x]=sz; par[sz]=fa; key[sz]=x; pushup(fa); splay(sz);return ; } } }
删除比较麻烦待会再说
2.查询x的排名
还是遵循key[now]比x小就往左子树找,否则就往右子树找的原则,直到找到
注意这里排名的定义是所有比x小的数的数量+1,如果有一个数q比x小,但是q出现了多次,那么重复出现的q也算作比x小的数(就是答案也包括那些重复出现的数辣)。
因此,往左子树搜,当前答案不变,往右子树搜,答案增加size[左子树]
因为重复的也算,所以在now转移前还要加cnt[now]
查到了要记得splay!!!

int findk(int x) { int rtn=0; int now=root; while(1) { if(key[now]>x)now=ch[now][0]; else { rtn+=(ch[now][0]?size[ch[now][0]]:0);//先加(不管是否找到) if(x==key[now]) { splay(now);//记住splay return rtn+1;//记住+1 } rtn+=cnt[now]; now=ch[now][1]; } } }
3.查询第k大的数
k边查边减
如果当前点的左子树的size>=k,则去左子树查,k-=size[左子树]
否则就去右子树查,当now的size[左子树]+cnt[now]>=k的时候就说明now的权值就是第k大的数
因为如果当前的now不是第k大的话,就会去左子树查,但是现在已经是在右子树查的阶段了

int kth(int x) { int now=root,rtn=0; while(1) { if(ch[now][0]&&size[ch[now][0]]>=x)now=ch[now][0]; else { int temp=size[ch[now][0]]+cnt[now]; if(temp>=x) { return key[now];//这回不用splay了 } x-=temp;now=ch[now][1]; } } }
4.找x的前驱/后继
我们在找前驱/后继之前先把x插入原平衡树种,找完以后再删掉,会很方便。
在插入中,我们已经把x splay到根了,所以我们在找前驱的时候,就从根的左儿子开始,一路找到左儿子右子树的叶子节点,就是前驱。
后继:从根的右儿子开始,一路找到右儿子的左子树的叶子节点即可

int pre() { int now=ch[root][0]; while(ch[now][1])now=ch[now][1]; return now; } int next() { int now=ch[root][1]; while(ch[now][0])now=ch[now][0]; return now; }
5.最复杂的删除X
情况比较多,咱慢慢来
先来一次findk(x),目的是把x旋到根(也可以直接splay(x))
1:x曾经出现过多次
对于这种情况,直接cnt--,size--
2:x只出现过1次
①:x没有儿子:直接clear(root)
②:x只有左儿子或者右儿子
让x唯一的儿子当根,并调整父子关系(x的儿子没有父亲神马的),clear(x)
③:最麻烦的情况,x两个儿子都有
把x的前驱转到根,让x的前驱继承x的右儿子(至于左儿子,在把x的前驱转到根的时候已经继承了),调整父子关系(x的右儿子认x的前驱神马的),clear(x)

void del(int x) { int sy=fink(x); if(cnt[root]>1) { cnt[root]--;pushup(root);return; } if(!ch[root][0]&&!ch[root][1]) { clear(root);root=0;return ; } if(!ch[root][0]) { int rt=root;root=ch[root][1];par[root]=0;clear(rt);return ; } else if(!ch[root][1]) { int rt=root;root=ch[root][0];par[root]=0;clear(rt);return ; } int rt=root;int pr=pre(); splay(pr); ch[root][1]=ch[rt][1]; par[ch[rt][1]]=root; clear(rt); pushup(root); }
模板题:洛谷P3369普通平衡树
更难一点的窝不会的文艺平衡树

#include<bits/stdc++.h> #define pa pair<int,int> using namespace std; inline int read() { char ch=getchar(); int x=0;bool f=0; while(ch<‘0‘||ch>‘9‘) { if(ch==‘-‘)f=1; ch=getchar(); } while(ch>=‘0‘&&ch<=‘9‘) { x=(x<<3)+(x<<1)+(ch^48); ch=getchar(); } return f?-x:x; } const int N=100009; int n,sz; int ch[N][2],par[N],key[N],cnt[N],size[N]; int root; void pushup(int x) { size[x]=size[ch[x][0]]+size[ch[x][1]]+cnt[x]; return ; } void clear(int x) { size[x]=0;ch[x][0]=0;ch[x][1]=0;key[x]=0;cnt[x]=0;par[x]=0; return ; } bool get(int x) { return ((ch[par[x]][1]==x)?1:0); } void rotate(int x) { int y=par[x],z=par[y],k=get(x),e=get(y); ch[y][k]=ch[x][k^1];par[ch[y][k]]=y; par[y]=x;ch[x][k^1]=y; par[x]=z; if(z) ch[z][e]=x; pushup(y);pushup(x); } void splay(int x) { for(int fa;fa=par[x];rotate(x)) if(par[fa]) rotate((get(x)==get(fa))?fa:x); root=x; } void insert(int x) { if(root==0) { sz++; key[sz]=x; root=sz; cnt[sz]=1;size[sz]=1; par[sz]=ch[sz][0]=ch[sz][1]=0; return; } int now=root,fa=0; while(1) { if(key[now]==x) { cnt[now]++; pushup(now); pushup(fa); splay(now);//当前节点旋转 return ; } fa=now; now=ch[now][key[now]<x]; if(now==0) { sz++; size[sz]=1;cnt[sz]=1; root=sz; key[sz]=x; ch[fa][key[fa]<x]=sz; par[sz]=fa; key[sz]=x; pushup(fa); splay(sz);return ; } } } int fink(int x) { int rtn=0; int now=root; while(1) { if(key[now]>x)now=ch[now][0]; else { rtn+=(ch[now][0]?size[ch[now][0]]:0); if(x==key[now]) { splay(now); return rtn+1; } rtn+=cnt[now]; now=ch[now][1]; } } } int kth(int x) { int now=root,rtn=0; while(1) { if(ch[now][0]&&size[ch[now][0]]>=x)now=ch[now][0]; else { int temp=size[ch[now][0]]+cnt[now]; if(temp>=x) { return key[now]; } x-=temp;now=ch[now][1]; } } } int pre() { int now=ch[root][0]; while(ch[now][1])now=ch[now][1]; return now; } int next() { int now=ch[root][1]; while(ch[now][0])now=ch[now][0]; return now; } void del(int x) { int sy=fink(x); if(cnt[root]>1) { cnt[root]--;pushup(root);return; } if(!ch[root][0]&&!ch[root][1]) { clear(root);root=0;return ; } if(!ch[root][0]) { int rt=root;root=ch[root][1];par[root]=0;clear(rt);return ; } else if(!ch[root][1]) { int rt=root;root=ch[root][0];par[root]=0;clear(rt);return ; } int rt=root;int pr=pre(); splay(pr); ch[root][1]=ch[rt][1]; par[ch[rt][1]]=root; clear(rt); pushup(root); } int main() { n=read(); for(int i=1;i<=n;i++) { int opt=read(),x=read();; if(opt==1)insert(x); if(opt==2)del(x); if(opt==3)printf("%d\n",fink(x)); if(opt==4)printf("%d\n",kth(x)); if(opt==5){insert(x);printf("%d\n",key[pre()]);del(x);} if(opt==6){insert(x);printf("%d\n",key[next()]);del(x);} } }
标签:编号 删除 include idt isp ret print splay return
原文地址:https://www.cnblogs.com/lcez56jsy/p/11229550.html