标签:turn abs 线性同余方程 col 限制 cout code 矩形 ret


我没忍住,还是搞了题目。
这个题特别强,强到炸。
我开始考场上面打了一个暴力,指DP,没关注负数,爆0了。
然后考后总结听的一脸懵逼。
翻了好多篇大佬的博客之后才磕磕巴巴的模仿的AC掉。
之后补充了很多知识之后,才来写的这篇博客。
这个题的知识应用不算生僻,但是也绝对不能算是熟悉。
并且用到的知识量很大。
1. 费马小定理。
2.中国剩余定理。
3.卢卡斯,或者扩展卢卡斯。
很多大佬的博客都写的很轻松,那么我就来写一篇初学小白是如何一步步想到这里的。
当然,肯定是有些玄学的。
首先引用G坑的一句话题意:
在坐标平面上,从 ( 0,0 ) 到 ( n,m ) , 恰好走了T步的方案数 (在走够T步之前可以经过点 ( n,m ) ) , 输出答案对MOD取模之后的答案。
这什么啊?搜索?
完全不理解啊,怎么办啊?
有一个问题:究竟能不能走出这个 n*m 的矩形去呢?
显然是可以的,不然就有可能无论怎么走 t 步都走不到。
然后可以发现一个小细节:求恰好走 t 步。【我第一次就没看出来
????能不能DP转移啊?
回去看看数据范围,额,DP是肯定会炸的,但是没思路就先打暴力啊。
这个时候我们考虑怎么设定状态。
当时时间紧急,我第一次设置的是走到点(i,j)走了k步的方案数,然后我想不到怎么转移,瞎胡写了一个之后TLE了。
赛后受到同机房大佬csy的指点,把状态转移方程改了改,就顺利搞到了30分。
这个DP还是蛮有难度的。
首先,刚刚我们注意到一个问题,行走范围没有限制,那么岂不是乱走一气?
那么数组下标就可能是负数。
所以我们要设置一个偏移量,让数组能够存的下我们的状态。
那么这个偏移量是多少呢?
我们观察数据,发现 n,m可以是负数,但是 t 不会。
所以在100的范围内,就算题目出到最坑,它上下方向最多也就只能走到-49去,左右同理。
好的,那么我们就把偏移量设做50就ok了。
接下来是转移方程的设定。
其实仔细想想就能发现,其实走到n,m就是在水平方向和竖直方向上分别贡献 n 和 m。
除了这些有效步数之外的 t - m - n 步,就一定要分成两部分,偏移和回转。【就是跑偏了就得跑回来
那么我们假设 f [ k ][ i ][ j ] 为走了k步之后,走到 i,j 的方案数。
那么每个点就是由它的四周转移过来的了。
#include<iostream> #include<cstdlib> #include<cstdio> #include<cstring> #include<algorithm> using namespace std; int dp[201][201][201]; int t,mod,n,m; int dx[5]={0,1,-1,0,0}; int dy[5]={0,0,0,1,-1}; int main() { scanf("%d%d%d%d",&t,&mod,&n,&m); n=abs(n); m=abs(m);//可能是负数 int p=50;//下标出现负数 dp[0][p][p]=1; int s=-((t-n-m)/2+1); int e=(t-n-m)/2+1; for(int k=1;k<=t;k++) for(int i=s;i<=t+n;i++) for(int j=s;j<=t+m;j++) for(int d=1;d<=4;d++) { dp[k][p+i][p+j]+=dp[k-1][i+p+dx[d]][j+p+dy[d]]; dp[k][p+i][p+j]%=mod; } cout<<dp[t][n+p][m+p]<<endl; return 0; }
好的暴力写完了,该出现一些有技术含量的东西了。
这么鬼畜的数据,一定是组合数学!!!【血的经验
好的,开始思考。
然后我们会发现:【其实并发现不了
对于一种方案,实际上是一个长度为T的指令序列,其中有上下左右四种指令
意思就是说,不同指令的数量和排列顺序,都会构成一个不同的路径。
那么我们猜想四个方向上行走的数量是有关系的。
假设上下左右的数量为a,b,c,d,且设 n,m 均为正数
则一种合法的恰能到达 ( n,m ) 的指令序列的数量属性一定满足:
a - b = m
d - c = n
显然刚刚说过的 a+b+c+d = T
这样的话,三个方程,四个未知数,我们只需要枚举一个未知数就可以全部表示出来。
然后再用多重集合的排列来算方案数即可。
你会多重集吗?
多重集就是emmm。
举个例子感性理解一下:
集合A中有 { a1, a2, a3, a4,..........,an };
表示有a1个1,a2个2,等等等等。
那么多重集的排列就是 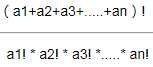
当我们打出来代码的时候,惊讶的发现,WA掉了。
这是为什么呢?仔细回去读题。
题目中最后一句,我们发现,mod数不一定是一个质数。
那怎么办啊?
大佬教我使用中国剩余定理。
然后学到了新的解题思路。
先将模数分解质因数,对于每一个质因子进行一次计算,最后再用中国剩余定理合并这些线性同余方程组。
(仅适用于满足——MOD为若干互不相同质数的乘积这一性质的取模运算)
分解质因数之后,对于每一个质因子跑一次上述算法,分别算出答案,最后再跑一下CRT就行了
但要注意,对于组合数取模时,当模数小于组合数运算中的阶乘数时,不能直接用阶乘和阶乘逆元计算
因为大于模数的数阶乘后一定含有该模数,故值一定为0,且并不能通过乘以逆元来还原(并没有逆元)
这时就要用 Lucas 定理来计算
还有一种更通用的处理模数的思路,就是扩展Lucas,可以一次算出答案【如果模数为任意自然数的话就必须用扩展Lucas了
但是我不会。QAQ
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> #include<algorithm> #define rint register int #define ll long long using namespace std; const int maxn=100005; ll t,n,m,p,a,b,c,d; ll fac[maxn],inv[maxn]; ll pri[30],ans[30],cnt; ll fpow(ll x,ll k,ll id) { ll ret=1; while(k) { if(k&1) ret=(ret*x)%pri[id]; k>>=1; x=(x*x)%pri[id]; } return ret%pri[id]; } ll C(ll x,ll y,ll id) { if(x<y) return 0; return fac[x]*inv[y]%pri[id]*inv[x-y]%pri[id]; } ll Lucas(ll x,ll y,ll id) { if(x<y) return 0; if(!x) return 1; return Lucas(x/pri[id],y/pri[id],id)*C(x%pri[id],y%pri[id],id)%pri[id]; } int main() { scanf("%lld%lld%lld%lld",&t,&p,&n,&m); m=abs(m); n=abs(n); if(t<n+m) { printf("0\n"); return 0; } if((t&1)!=((n+m)&1)) { printf("0\n"); return 0; } for(rint i=2;i*i<=p;i++) { if(!(p%i)) { p/=i; pri[++cnt]=i; } } if(p>1) pri[++cnt]=p; for(rint i=1;i<=cnt;i++) { ll x=min((ll)t,pri[i]-1); inv[0]=fac[0]=fac[1]=1; for(rint j=2;j<=x;j++) fac[j]=(fac[j-1]*j)%pri[i]; inv[x]=fpow(fac[x],pri[i]-2,i); for(rint j=x-1;j>=1;j--) inv[j]=(inv[j+1]*(j+1))%pri[i]; int j=m; while(1) { a=j; b=a-m; c=(t-2*a+n+m)/2; d=c-n; j++; if(d<0) break; ans[i]=(ans[i]+Lucas(t,a,i)*Lucas(t-a,b,i)%pri[i]*Lucas(t-a-b,c,i)%pri[i])%pri[i]; } } ll mod=1; for(rint i=1;i<=cnt;i++) mod*=pri[i]; ll x,y,ret=0; for(rint i=1;i<=cnt;i++) { ll tmp=mod/pri[i]; y=fpow(tmp,pri[i]-2,i); ret=(ret+y*tmp%mod*ans[i]%mod)%mod; } ll ans=(ret%mod+mod)%mod; printf("%lld\n",ans); return 0; }
AC!!!!!!!!!!!
标签:turn abs 线性同余方程 col 限制 cout code 矩形 ret
原文地址:https://www.cnblogs.com/qxyzili--24/p/11231021.html