标签:梯度下降法 最小 display 批量 随机梯度 直接 image 降维 比例
(1)情景:给定一定数量的数据点,通过拟合得到其回归直线,使得所有点到这个直线的距离之和(损失函数)最小。
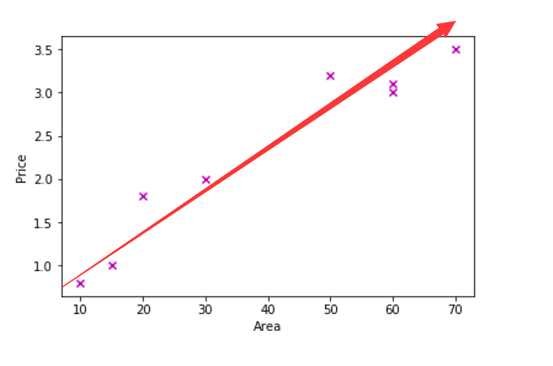
即:已知各个点的坐标,反求直线表达式的最优系数解。
假定直线参数为θ,则直线表达式为:
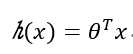
得到的直线(平面)表达式应使得损失函数最小,其中损失函数表达式:
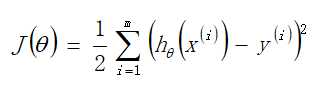
(2)求解方式:
第一种:直接求解
欲使损失函数最小,对损失函数进行求导等于0(实际问题中极小值即为最小值)
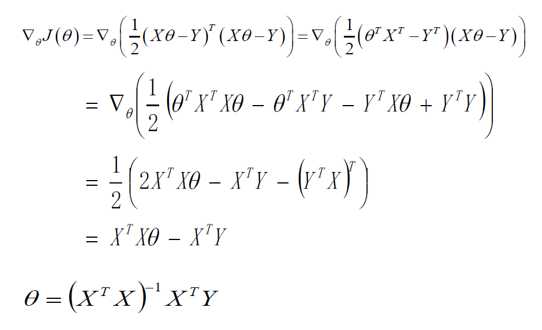
第二种:梯度下降法
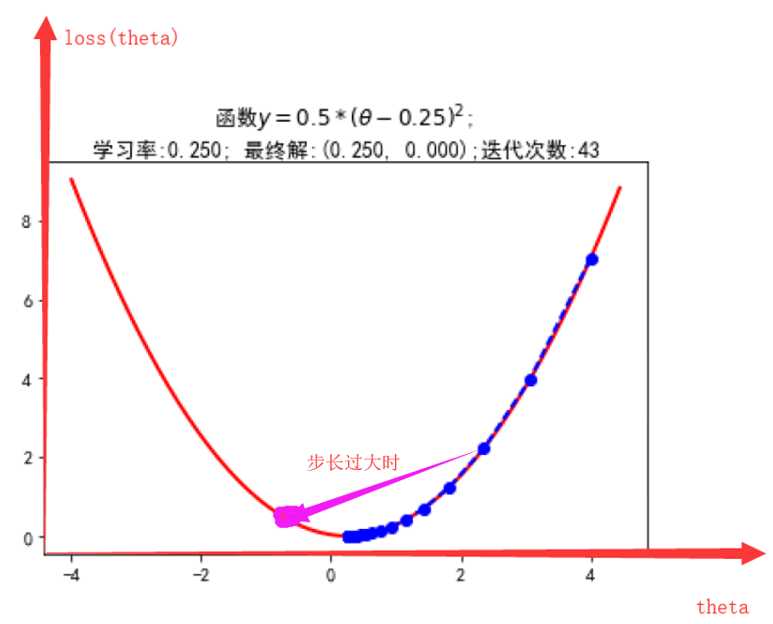
从损失函数上的任一点出发,每次沿梯度的方向更新θ的值,所得到的新的θ将会使损失函数的函数值更小。(属随机梯度下降原理)
求解的关键在于得到其导数的方向,保证每次更新都将沿损失函数值下降的方向,同时要选取适当的学习步长α,避免过快更新超过其最小值的同时尽量选择较大步长来减少迭代更新的次数。
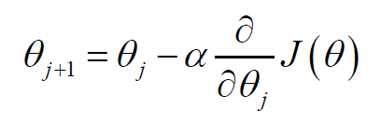
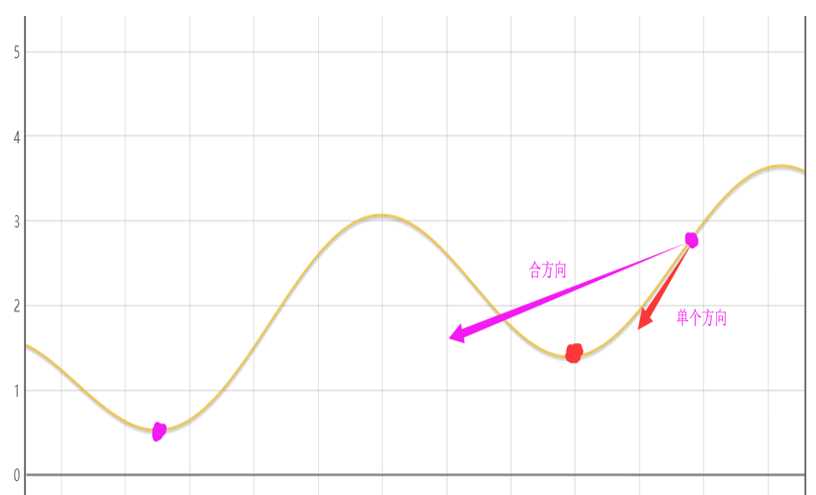
上面的所述的思想,是基于每次都代入一个x进行迭代更新,称为随机梯度下降,但由于其方向为单个的导数的方向,所得到的极值点可能为局部最小值(如下图所示),而非整体最小值,想尽可能 得到整体最小值 ,应采用批量梯度下降法,即每次更新均代入所有的X进行更新,其更新的方向为合导数的方向(可以理解为合力与分力的关系,站在更高维度去思考该问题,合力方向与单个方向的不同将使得各个维度的变化量不同)。
1.2 算法流程
(1)解析解
直接计算可得
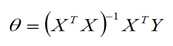
(2)梯度下降法

其中,当采用随机梯度下降时,步骤2为:
![]()
当采用批量梯度下降时,步骤2为:
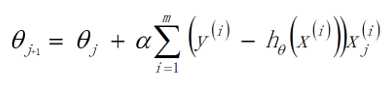
1.3 注意事项
(1)解析解的求解要求 可逆,当它不可逆时:
可逆矩阵要求方阵的行列式为0,要求矩阵满秩,应去除共线性的特征和多余特征
1)考虑是否存在多余特征,去掉多余特征
2)降维去除共线性的特征(呈比例关系的特征)
3)加入惩罚项保证可逆
(2)为防止回归得到的模型过拟合,应在损失函数中加入正则项
正则项有分L1正则(Lasso回归)与L2正则(岭回归)
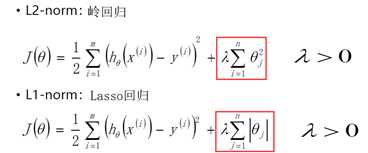
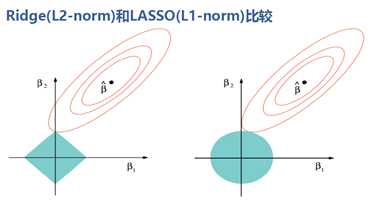
加入正则项后,所得导数方向为原函数与正则项的切点方向,由于L1正则项的导数方向较少,故加入L1正则项后得到的解其0值较多(忽略了较多维度的影响)

标签:梯度下降法 最小 display 批量 随机梯度 直接 image 降维 比例
原文地址:https://www.cnblogs.com/wenghsimu/p/11231443.html