标签:std ios 二维 算法 自己 没有 color using 允许
1 for (i = 1; i <= n; i++) 2 { 3 for (j = 1; j <= n; j++) 4 { 5 if (e[i][j] > e[i][1] + e[1][j]) 6 e[i][j] = e[i][1] + e[1][j]; 7 } 8 }
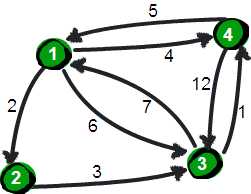
但是事实上我们不仅仅只允许经过1号顶点,求任意两点之间的最短路径。
简而言之就是:从i号顶点到j号顶点只经过前k号点的最短路程。
那么关于k的这个循环我们到底是放在最外面还是放在里面呢?这个就需要我们对FLyod算法有更深一步的认识。这个算法实际上是个动态规划算法

正因为如此所以我们的 k 自然要放在最外面了!
核心代码:
1 for(k=1;k<=n;k++) 2 for(i=1;i<=n;i++) 3 for(j=1;j<=n;j++) 4 if(e[i][j]>e[i][k]+e[k][j] ) 5 e[i][j]=e[i][k]+e[k][j];
整体的代码:
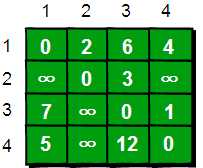
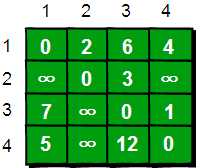
1 #include <cstdio> 2 #include <cstring> 3 #include <iostream> 4 #include <algorithm> 5 #include <set> 6 #include <queue> 7 8 #define LL long long 9 using namespace std; 10 const int MAXN = 100; 11 12 int main() 13 { 14 int e[10][10],k,i,j,n,m,t1,t2,t3; 15 int inf=99999999; //用inf(infinity的缩写)存储一个我们认为的正无穷值 16 //读入n和m,n表示顶点个数,m表示边的条数 17 scanf("%d %d",&n,&m); 18 //初始化 19 for(i=1;i<=n;i++) 20 for(j=1;j<=n;j++) 21 if(i==j) e[i][j]=0; 22 else e[i][j]=inf; 23 //读入边 24 for(i=1;i<=m;i++) 25 { 26 scanf("%d %d %d",&t1,&t2,&t3); 27 e[t1][t2]=t3; 28 } 29 //Floyd-Warshall算法核心语句 30 for(k=1;k<=n;k++) 31 for(i=1;i<=n;i++) 32 for(j=1;j<=n;j++) 33 if(e[i][j]>e[i][k]+e[k][j] ) 34 e[i][j]=e[i][k]+e[k][j]; 35 //输出最终的结果 36 for(i=1;i<=n;i++) 37 { 38 for(j=1;j<=n;j++) 39 { 40 printf("%10d",e[i][j]); 41 } 42 printf("\n"); 43 } 44 return 0; 45 }
标签:std ios 二维 算法 自己 没有 color using 允许
原文地址:https://www.cnblogs.com/-Ackerman/p/11237114.html