标签:用户 blank 阈值 平衡 button ica 测试数据 nbsp 垃圾邮件
之前介绍了这么多分类模型的性能评价指标(《分类模型的性能评价指标(Classification Model Performance Evaluation Metric)》),那么到底应该选择哪些指标来评估自己的模型呢?答案是应根据应用场景进行选择。
查全率(Recall):recall是相对真实的情况而言的:假设测试集里面有100个正类,如果模型预测出其中40个是正类,那模型的recall就是40%。查全率也称为召回率,等价于灵敏性(Sensitivity)和真正率(True Positive Rate,TPR)。

查全率的应用场景:需要尽可能地把所需的类别检测出来,而不在乎结果是否准确。比如对于地震的预测,我们希望每次地震都能被预测出来,这个时候可以牺牲precision。假如一共发生了10次地震,我们情愿发出1000次警报,这样能把这10次地震都涵盖进去(此时recall是100%,precision是1%),也不要发出100次警报,其中有8次地震给预测到了,但漏了2次(此时recall是80%,precision是8%)。
查准率(Precision):precision是相对模型的预测结果而言的:假设模型一共预测出了100个正类,其中80个是正确的,那么precision就是80%。

查准率的应用场景:需要尽可能地把所需的类别检测准确,而不在乎这些类别是否都被检测出来。比如对于罪犯的预测,我们希望预测结果是非常准确的,即使有时候放过了一些真正的罪犯,也不能错怪一个好人。
F1:F1 score是对查准率和查全率取平均,但是这里不是取算数平均,而是取调和平均。为什么?因为调和平均值更接近较小值,这样查准率或查全率中哪个值较小,调和平均值就更接近这个值,这样的测量指标更严格。

 或
或 
F1的应用场景:在precision和recall两者要求同样高的情况下,可以用F1来衡量。
查全率和查准率是最常用的两个分类指标,除此之外人们还会用到以下一些指标:
(注:查全率在医学上经常被称为真阳性率(True Positive Rate,TPR)。)
假阳性率(False Positive Rate,FPR):在医学上又称误诊率,等于 1 - 特异性(Specificity)。
假阴性率(False Negative Rate,FNR):在医学上又称漏诊率,等于 1 - 灵敏性(Sensitivity)。
在现实中,人们往往对查全率和查准率都有要求,但是会根据应用场景偏向某一边。比如做疾病检测,我们希望尽可能地把疾病检测出来,但同时也不想检测结果的准确率太低,因为这样会造成恐慌和不必要的医疗支出(偏向recall)。又比如对于垃圾邮件检测(Spam Detection),我们希望检测出的垃圾邮件肯定是垃圾邮件,而不希望把正常邮件邮件归为垃圾邮件,因为这样有可能会给客户造成很大的损失,但是相对地,如果我们经常把垃圾邮件归为正常邮件,虽然不会造成很大损失,但是会影响用户体验(偏向precision)。再比如如果是做搜索,搜出来的网页都和关键词相关才是好的搜索引擎,在这种情况下,我们希望precision高一些(偏向precision)。这时就要用到PR曲线。
PR曲线:x轴为查全率,y轴为查准率。
PR曲线的应用场景:需要根据需求找到对应的precision和recall值。如果偏向precison,那就是在保证recall的情况下提升precision;如果偏向recall,那就是在保证precision的情况下提升recall。比如对于欺诈检测(Fraud Detection),如果要求预测出的潜在欺诈人群尽可能准确,那么就要提高precision;而如果要尽可能多地预测出潜在的欺诈人群,那么就是要提高recall。一般来说,提高二分类模型的分类阈值就能提高precision,降低分类阈值就能提高 recall,这时便可观察PR 曲线,根据自己的需要,找到最优的分类阈值(threshold)。
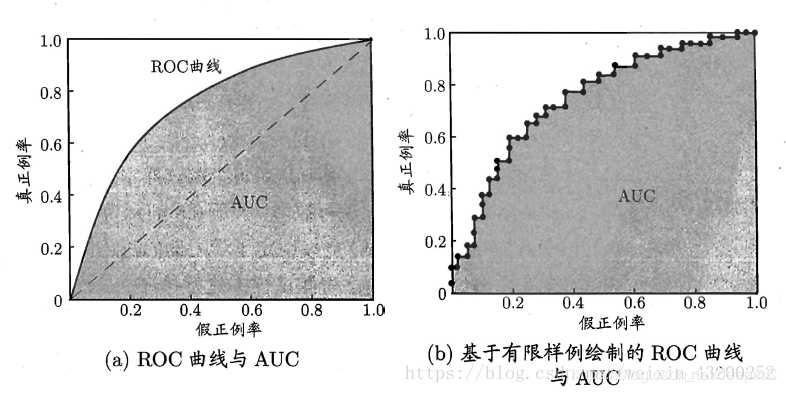
一般来说,模型的ROC-AUC值越大,模型的分类效果越好。不过如果两个模型AUC值差不多,并不代表这两个模型的效果相同。下面两幅图中两条ROC曲线相交于一点,AUC值几乎一样:当需要高Sensitivity时,模型A(细线)比B好;当需要高Speciticity时,模型B(粗线)比A好。
总结一下PR曲线和ROC曲线&AUC的区别:
1. PR曲线在正负样本比例比较悬殊时更能反映分类器的性能。当正负样本差距不大的情况下,ROC和PR的趋势是差不多的,但是当负样本很多的时候,两者就截然不同了,ROC效果依然看似很好,但是PR上反映效果一般。这就说明对于类别不平衡问题,ROC曲线通常会给出一个过于乐观的效果估计,此时还是用PR曲线更好。
2. ROC曲线由于兼顾正例与负例,适用于评估分类器的整体性能(通常是计算AUC,表示模型的排序性能);PR曲线则完全聚焦于正例,因此如果我们主要关心的是正例,那么用PR曲线比较好。
3. ROC曲线不会随着类别分布的改变而改变。然而,这一特性在一定程度上也是其缺点。因此需要根据不用的场景进行选择:比如对于欺诈检测,每个月正例和负例的比例可能都不相同,这时候如果只想看一下分类器的整体性能是否稳定,则用ROC曲线比较合适,因为类别分布的改变可能使得PR曲线发生变化,这种时候难以进行模型性能的比较;反之,如果想测试不同的类别分布对分类器性能的影响,则用PR曲线比较合适。
总的来说,我们应该根据具体的应用场景,在相应的曲线上找到最优的点,得到相对应的precision,recall,f1 score等指标,然后去调整模型的分类阈值,从而得到一个符合具体应用的模型。
附:
如何画PR曲线?
根据每个测试样本属于正样本的概率值从大到小排序,依次将这些概率值作为分类阈值,当测试样本属于正样本的概率大于或等于这个threshold时,我们认为它为正样本,否则为负样本。每次选取一个不同的threshold,我们就可以得到一组recall和precision,即PR曲线上的一点。取n组不同的分类阈值,就可以得到n个点,连接起来就成为一条曲线。threshold取值越多,PR曲线越平滑。
如何画ROC曲线?
根据每个测试样本属于正样本的概率值从大到小排序,依次将这些概率值作为分类阈值,当测试样本属于正样本的概率大于或等于这个threshold时,我们认为它为正样本,否则为负样本。每次选取一个不同的threshold,我们就可以得到一组FPR和TPR,即ROC曲线上的一点。取n组不同的分类阈值,就可以得到n个点,连接起来就成为一条曲线。threshold取值越多,ROC曲线越平滑。
如何计算AUC值?
假定ROC曲线是由坐标为 的点按序连接而形成,则AUC可估算为:
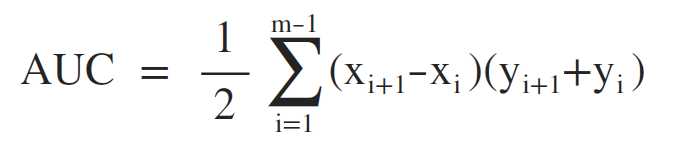
查全率(Recall),查准率(Precision),灵敏性(Sensitivity),特异性(Specificity),F1,PR曲线,ROC,AUC的应用场景
标签:用户 blank 阈值 平衡 button ica 测试数据 nbsp 垃圾邮件
原文地址:https://www.cnblogs.com/HuZihu/p/11146557.html