Bezier曲线(1)：Introducion

标签：引入   isp   win   drawing   page   rac   定义   VID   span   

搬运自我的CSDN https://blog.csdn.net/u013213111/article/details/94067849

参考：
贝塞尔曲线扫盲
贝塞尔曲线的理解
使用贝塞尔曲线绘制多点连接曲线
Bezier curves and surfaces
Bezier Curve Drawing Algorithms
Construction of Bézier Curves

首先来直观地看一下Bezier曲线是什么样的。
这是个二次Bezier曲线，经过 \(P_0\) 和 \(P_2\) 这个两个点，并且受到 \(P_1\) 点的牵引：

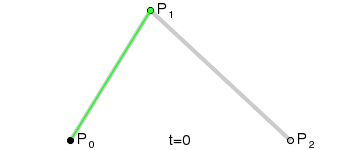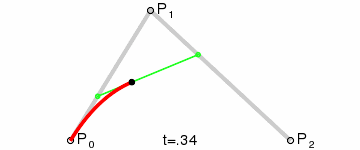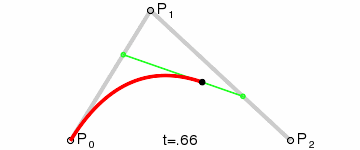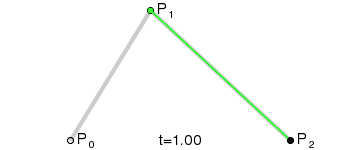
曲线的表达式也极为美观：
\[ C(t) = (1-t)^2 P_0 + t(1-t)P_1+t^2P_2，t \in [0,1] \]
(C means curve)

其实这么一看应该也就能理解Bezier曲线的思想了，也就是给与数据点不同的“权重”来计算出的一种曲线，这些点和权重决定了曲线的某种走势。

给出个稍微严格点的定义吧：
给定空间中的n+1个点 \(P_0\) ，\(P_1\)，\(P_2\)，...和 \(P_n\)，由这些点定义的Bezier曲线是
\[ C(u) = \sum_{i=0}^n B_{n,i} (u) P_i\]
其中，\(B_n,_i (u) = \frac{n!}{i!(n-i)!}u^i(1-u)^{n-i}\)，也被称为Bernstein多项式。

由Bernstein多项式来计算Bezier曲线是显而易见的的方法，然而这种方法并不是数值稳定的（会引入数值计算误差），因此在实际中，通常采用的是de Casteljau算法。

Bezier曲线(1)：Introducion

标签：引入   isp   win   drawing   page   rac   定义   VID   span   

原文地址：https://www.cnblogs.com/lyrich/p/11241587.html