数学优化

标签：near   crete   必须   不等式   离散   标签   去掉   最优化问题   img   

数学优化（Mathematical Optimization）问题，也叫最优化问题，是指在一定约束条件下，求解一个目标函数的最大值（或最小值）问题。

数学优化问题的定义为：给定一个目标函数（也叫代价函数）f : A → R，寻找一个变量（也叫参数）x^∗ ∈ D，使得对于所有D中的x，f(x^∗) ≤ f(x)（最小化）；或者f(x^∗) ≥ f(x)（最大化），其中D为变量x 的约束集，也叫可行域；D中的变量被称为是可行解。

数学优化的类型

离散优化问题

离散优化（Discrete Optimization）问题是目标函数的输入变量为离散变量，比如为整数或有限集合中的元素。离散优化问题的求解一般都比较困难，优化算法的复杂度都比较高。离散优化问题主要有两个分支：

　　1. 组合优化（Combinatorial Optimization）：其目标是从一个有限集合中找出使得目标函数最优的元素。在一般的组合优化问题中，集合中的元素之间存在一定的关联，可以表示为图结构。典型的组合优化问题有旅行商问题、最小生成树问题、图着色问题等。很多机器学习问题都是组合优化问题，比如特征选择、聚类问题、超参数优化问题以及结构化学习（Structured Learning）中标签预测问题等。

　　2. 整数规划（Integer Programming）：输入变量x ∈ Z^d 为整数。一般常见的整数规划问题为整数线性规划（Integer Linear Programming，ILP）。整数线性规划的一种最直接的求解方法是：

　　　　（1）去掉输入必须为整数的限制，将原问题转换为一般的线性规划问题，这个线性规划问题为原问题的松弛问题；

　　　　（2）求得相应松弛问题的解；

　　　　（3）把松弛问题的解四舍五入到最接近的整数。但是这种方法得到的解一般都不是最优的，因此原问题的最优解不一定在松弛问题最优解的附近。另外，这种方法得到的解也不一定满足约束条件。

连续优化问题

连续优化（Continuous Optimization）问题是目标函数的输入变量为连续变量x ∈ R^d，即目标函数为实函数。

无约束优化和约束优化

在连续优化问题中，根据是否有变量的约束条件，可以将优化问题分为无约束优化问题和约束优化问题。

　　无约束优化问题：可行域为整个实数域D = R^d，可以写为

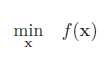
　　其中x ∈ R^d 为输入变量，f : R^d → R为目标函数。

　　约束优化问题：变量x需要满足一些等式或不等式的约束。约束优化问题通常使用拉格朗日乘数法来进行求解。

最优化问题一般可以表示为求最小值问题。求f(x) 最大值等价于求−f(x) 的最小值。

数学优化

标签：near   crete   必须   不等式   离散   标签   去掉   最优化问题   img   

原文地址：https://www.cnblogs.com/callyblog/p/11250845.html