标签：数组   表示   最小   个数   进制   函数   传递   如何   区间查询   

-1.问题内容

考虑以下问题：

给定\(a_1\)~\(a_n\),有m次操作，每次操作有两种情况：

• 修改\(a_i\)的值

• 求\(a_i\)~\(a_j\)中最小的数

注意

这个例题求的是最小值，而网上的大部分例题都是求和，所以在之后的代码中看到很多min不要奇怪为什么不是+=,因为题目是求最小值qwq

所用数据结构当然是线段树了。

0.代码片段：上传

上传操作：当左右孩子都修改好之后，更改父节点的值

代码实现

void pushup(int id){
    minv[id]=min(minv[id<<1],minv[id<<1|1]);//父节点的值更新为左右孩子中更小的那一个
}

这段代码在之后的几段代码中都会用到

调用方法

pushup(id);//这会将节点id的左孩子和右孩子的值上传到他们的父节点（也就是节点id）上

1.建树

树的形态

像这样：

思路

建树显然是一个递归的过程：如果是叶子节点，直接建；否则，递归左孩子和右孩子，然后将父节点根据左孩子和右孩子的值来更新(在这道题目中是取左孩子和右孩子的值的最小值)

代码实现

const int maxn = 10010;
int minv[4 * maxn], a[maxn];
//数组minv用来存储线段树中每个节点所存储的区间最小值；数组a用来存储输入的a1~an

// id 表示结点编号，l, r 表示左右区间
void build(int id, int l, int r) {
    if (l == r) {//这是一个叶子节点
        minv[id] = a[l];//叶子节点存储的值自然就是a数组中的这个数
        return;//记得return掉！！！
    }
    int mid = (l + r) >> 1;
    build(id << 1, l, mid);//递归建树左孩子
    build(id << 1 | 1, mid + 1, r);//递归建树右孩子(这个二进制操作意思就是id*2+1)
    pushup(id);//上传
}

调用方法

build(1,1,n);

注意点

• 线段树必须开四倍空间(记住就好了。。。。。。)

• id<<1|1 一定不能写成id<<1+1,因为加法优先级比位移更高

2.单点修改-无lazy标记

思路

一个点的修改，只会影响到这棵线段树上的一根链。比如说修改\(a[6]\):

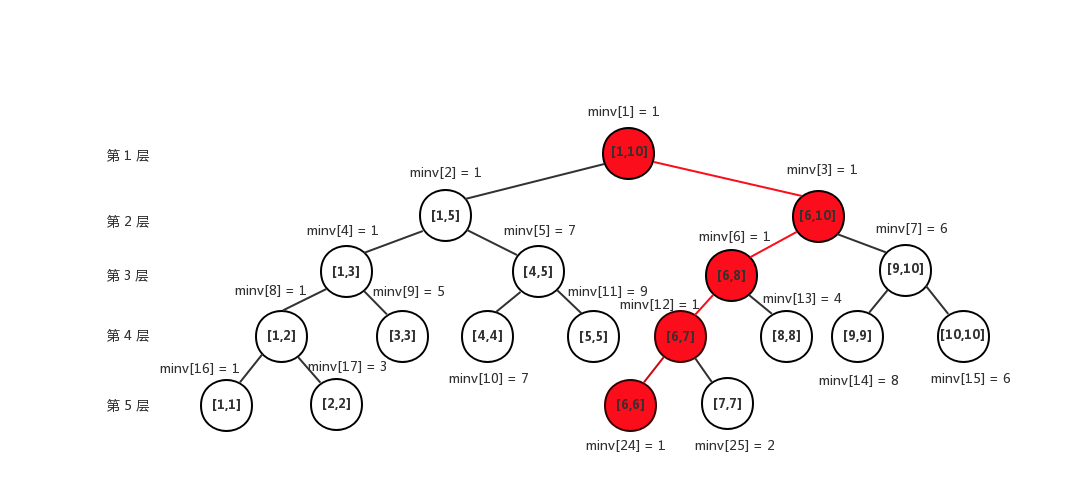
只有红色的点需要修改。

代码实现

// 把 a[x] 更改成 v
void update(int id, int l, int r, int x, int v) {
    if (l == r) {//这是一个叶子节点，并且一定是a[x](不信的话观察上面那根红链，只可能有一个叶子节点，并且那一定是a[x])
        minv[id] = v;//直接更新
        return;//一定要return掉！！！
    }
    int mid = (l + r) >> 1;
    if (x <= mid) {//a[x]在左区间，那么只有左区间需要更新
        update(id << 1, l, mid, x, v);
    } else {//否则，a[x]在右区间，那么只有右区间需要更新
        update(id << 1 | 1, mid + 1, r, x, v);
    }
    pushup(id);//执行完上面的if-else之后，子节点该更新的都更新好了，那么上传，以更新父节点
}

调用方法

使用update(1,1,n,x,v)对该函数进行调用

时间复杂度分析

• 时间复杂度：\(O(log\ n)?\)

一般情况下，认为树的最大深度为\(log\ n\),那么我们更新的链的长度最长就是$log?n \(,因此时间复杂度是\)O(log?n )$

3.单点查询-无lazy标记

特别之处

单点查询其实是区间查询的特殊情况。因此略微了解一下即可。

思路

• 和单点修改几乎没什么两样。从根节点开始，跟着这条链从上往下走，直到碰到了叶子节点，那么就查询到了，返回即可

代码实现

int query(int id, int l, int r, int x) {
    if (l == r) {//查询到了
        return minv[id];//返回即可
    }
    int mid = (l + r) >> 1;
    if (x <= mid) {//a[x]在左区间
        return query(id << 1, l, mid, x);//对左区间进行查询
    } else {//否则，a[x]在右区间
        return query(id << 1 | 1, mid + 1, r, x);//对右区间进行查询
    }
}

调用方法

query(1,1,n,x);

时间复杂度分析

\(O(log\ n)\):同单点修改的时间复杂度

4.区间查询-无lazy标记

思路

对于查询区间\([x,y]\),其实就是查询树上的一些节点，最后将这些节点取最小值(为什么是最小值？见 问题内容-注意)

比如查询区间\([3,6]?\):

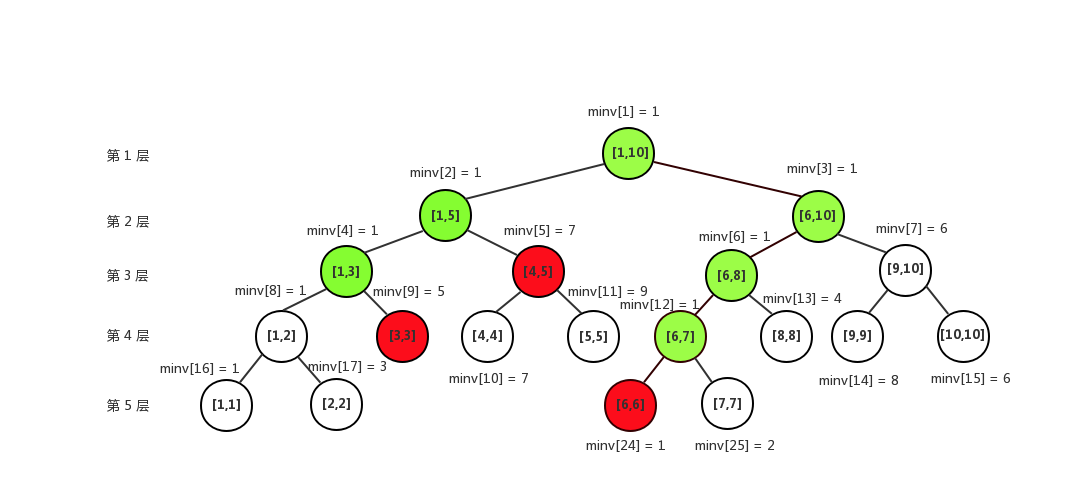
图中，绿色的节点会被递归查询到；红色的节点被区间\([3, 6]?\)完全包含，最终会在这些红点中取最小值。

具体做法：

• 碰到红点，直接返回
• 碰到绿点，进行以下判断：红点会出现在这个点的右孩子上还是左孩子上？往会出现红点的那个方向递归查询

代码实现

//为什么是最小值？因为题目中说查询的是[x,y]中的最小值。。。（然而网上大部分例题都是求和）所以不要奇怪。。题目是这么说的qwq
int query(int id, int l, int r, int x, int y) {
    if (x <= l && r <= y) {  // 如果完全包含，直接返回(这是一个红点)
        return minv[id];
    }
    int mid = (l + r) >> 1;
    int ans = inf;//重要！！！因为题目中说的是询问[x,y]中的 最小值！！！所以ans初始化为无穷大！！
    if (x <= mid) {
        ans = min(ans, query(id << 1, l, mid, x, y));  // 如果左区间包含，递归的查询左子树，并取最小值
    }
    if (y > mid) {
        ans = min(ans, query(id << 1 | 1, mid + 1, r, x, y));  // 如果右区间包含，递归的查询右子树，并取最小值
    }
    return ans;
}

调用方法

query(1,1,n,l,r);

时间复杂度分析

时间复杂度\(O(log\ n)\)

5.区间修改-有lazy标记

思路

糟糕的思路--利用单点修改实现区间修改

最坏情况：需要修改的区间是\([1, n]\),那么需要修改\(n\)次，每次复杂度\(log\ n\)，总复杂度\(O(nlog\ n)\)比推倒了重新建树(\(O(n)\))还要糟糕。

正解--lazy标记(即懒惰标记或者延迟标记)

基本思想

加入需要更新的区间是\([3, 5]\),那么让我们考虑下面这棵树：

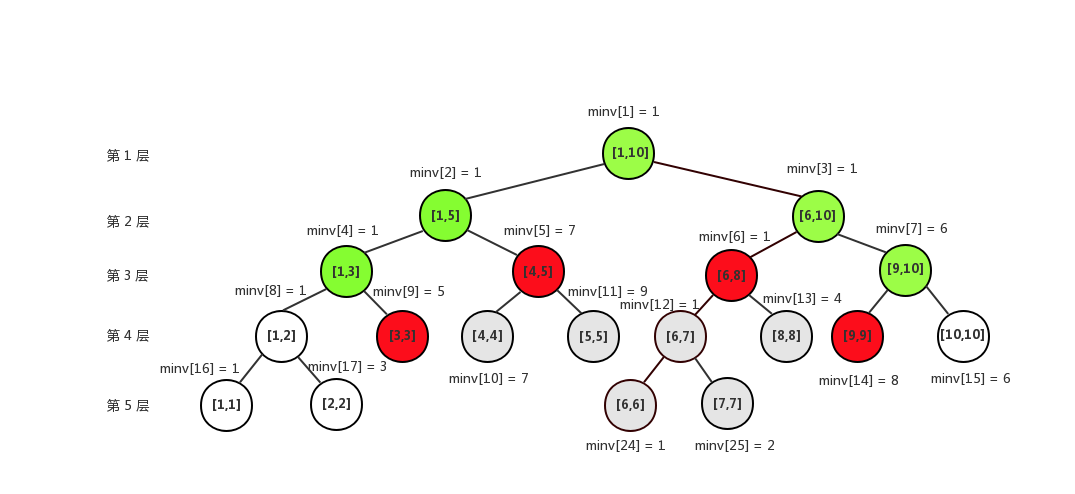
• 对于绿点，显然要继续递归更新；

• 对于红点：我们不进行递归更新，而是将延迟标记存下来，红点的子节点（灰点）不管：否则，就和推倒了重新建树一样了。那么，延迟标记如何理解？

引理

• 如果一个区间被整体加上了v，那么这个区间的最小值也会加上v：该引理显然成立

如何使用

对于红点，我们标记整个区间需要加上v，而不管灰点。这样可以保证红点的信息一定正确，不过灰点的信息不一定正确：但是暂时用不上它们

正确性

• 因为红点信息一定正确，那么红点的祖先在pushup后的信息也一定正确

• 虽然灰点的信息可能不正确，但是不要紧：我们暂时用不上。那么要是需要用了呢？

向下传递(pushdown)

1. 将延迟标记传递到左右孩子上（注意：延迟标记在左右孩子上可以累加）
2. 将左右孩子对应的值（也就是区间最小值）加上父节点的延迟标记的数值（正确性见引理）
3. 父节点延迟标记清零

代码实现

void pushup(int id) {//该函数用来处理向上传递
    minv[id] = min(minv[id << 1], minv[id << 1 | 1]);
}
void pushdown(int id) {//该函数用来处理向下传递
    // 如果有延迟标记，向下传递
    if (lazy[id]) {//如果有延迟标记的话
        lazy[id << 1] += lazy[id];
        lazy[id << 1 | 1] += lazy[id];//传递到左右孩子上
        minv[id << 1] += lazy[id];
        minv[id << 1 | 1] += lazy[id];//左右孩子对应的值(也就是区间最小值)加上父节点的延迟标记
        lazy[id] = 0;//重要！！！父节点延迟标记清零！！！
    }
}
void update(int id, int l, int r, int x, int y, int v) {
    if (x <= l && r <= y) {  // 如果完全包含，对该区间进行延迟标记。这是一个红色节点！！
        lazy[id] += v;//累加延迟标记
        minv[id] += v;//重要！！该区间的最小值一定得加上v(正确性见引理)。该操作可以保证红色节点的信息一定是正确的！！！
        return;//不进行继续递归
    }
    pushdown(id);  // 需要用到一个(可能是在之前的update操作中造成的)灰色节点，将父节点的延迟标记下传才能保证该节点的正确性
    int mid = (l + r) >> 1;
    if (x <= mid) {
        update(id << 1, l, mid, x, y, v);  // 如果左区间包含，递归更新左子树
    }
    if (y > mid) {
        update(id << 1 | 1, mid + 1, r, x, y, v);  // 如果右区间包含，递归更新右子树
    }//这两个if语句同区间查询
    pushup(id);//这一步可以保证红点的祖先节点的信息都是正确的！！
}

调用方法

update(1,1,n,x,y,v);

时间复杂度分析

时间复杂度同区间查询(这应该是很好理解吧。。代码长得那么想，连if语句都一样)，因此是\(O(log\ n)\)

实在不行记住即可(线段树的操作除了建树基本上时间复杂度都是\(O(log\ n)\)...应该很好记吧)

6.使用lazy标记之后其他操作代码的变化

变化内容

可以说基本没变。。。就是除了建树以外的每个操作中加上pushdown(id)这句话。

以区间查询为例

代码如下：

int query(int id, int l, int r, int x, int y) {
    if (x <= l && r <= y) {
        return minv[id];
    }
    pushdown(id);  // 和单点更新的唯一一点区别(pushdown为什么不放在上面那个if语句的前面？见代码解释)
    int mid = (l + r) >> 1;
    int ans = inf;
    if (x <= mid) {
        ans = min(ans, query(id << 1, l, mid, x, y));
    }
    if (y > mid) {
        ans = min(ans, query(id << 1 | 1, mid + 1, r, x, y));
    }
    return ans;
}

代码解释

对于代码中的那个问题，解释如下：

别忘了，延迟标记仅仅在需要维护正确性的前提下才需要向下传递！那么：

• 对于query函数，显然是保证了只要query到了编号为id的节点，那么编号为id的节点的信息就是正确的
• 函数头的那个if语句是说，如果这是一个红点，直接返回
• 但是pushdown维护的是编号为id的节点的子节点的正确性
• 但是如果符合那个if语句的条件（也就是这是一个红点），那么它的子节点显然就不用管了
• 所以pushdown要放在那个if语句后。这样可以节省时间
• 对于其他要用到这个if语句的操作，同理

线段树详解

标签：数组   表示   最小   个数   进制   函数   传递   如何   区间查询   

原文地址：https://www.cnblogs.com/LJB00125/p/xianduanshu-xiangjie.html