标签：并集 规则 假设 创建 white 乘法 mamicode document may
博主接触机器学习算法不久，借此记录一下学习过程。
朴素贝叶斯是贝叶斯决策的一部分，先让我们了解一下贝叶斯理论。假设我们有一个数据集，它由两类数据组成，数据分布如图所示：
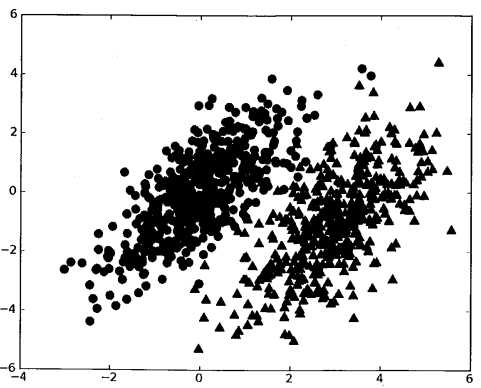
我们现在用p1(x,y)表示点(x,y)属于类别1（图中用圆点表示的类别）的概率，用p2(x,y)表示点(x,y)属于类别2（图中用三角形表示的类别）的概率，那么当一个新的数据点(x,y)，可以用以下规则判断它的类别：
当p1(x,y)>p2(x,y)，该数据点属于类别1；
当p1(x,y)<p2(x,y)，该数据点属于类别2。
贝叶斯决策理论的核心思想就是：
1.已知类条件概率密度参数和先验概率
2.利用贝叶斯公式转换为后验概率
3.根据后验概率的大小进行决策分类
在介绍贝叶斯公式之前，让我们先来回顾一下条件概率和全概率公式。
条件概率
定义：假设A,B是两个事件，p(A)>0,称 
为在已知事件B发生的条件下事件A发生的概率。
举个例子，假设一个桶里有3白4黑七个球，每个球形状大小完全相同即相互独立。如果从这个桶里随机取出1个球，那么取出黑球的概率p(black)为4/7，取出白球的概率p(white)为3/7。
如果这七个小球以下图方式存放，我们该如何计算上述概率呢？
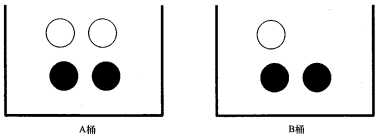
当我们事先知道小球所在桶的类别会改变时，我们便可以用条件概率来计算p(black)和p(white)。我们称小球出自A桶为事件A，小球出自B桶为事件B，则概率p(black|A)我们可以称作”在已知小球出自A桶的情况下，取出黑球的概率“。我们很容易得到p(black|A)=2/4，p(black|B)=2/3。
条件概率的计算公式如下：
p(black|A) = p(black,A)|p(A)
其中p(black,A)=2/7，p(A) = 4/7,故p(black|A) = 2/4;同理可得p(black/B)=2/3。
设A为一个事件，C1,C2,C3,...Cn为样本空间S的一个完备事件组：(1)Ci ∩ Cj=∅ ,i≠j (2)C1∪C2∪…∪Cn=S，则由全概率公式可得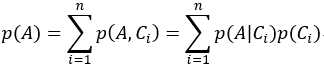
。实际问题中p(A)不容易求出，但却容易找到样本S的一个划分C1,C2,C3,...,Cn,且C1,C2,C3,...,Cn之间相互独立，这也是”朴素“一词的由来，不考虑数据特征间的关系，单纯认为特征是相互独立的。故我们可以通过得到p(A|Ci)和p(Ci)来求出p(A)。
通过条件概率公式和全概率公式，我们可以得到贝叶斯公式如下所示：
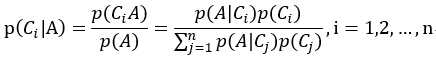
最终求出p(类别1|特征)，p(类别2|特征)等，比较各概率大小，进行分类。
实际应用场景：
1.文本分类
2.垃圾邮件过滤
3.病人分类
4.拼写检查
代码实现
基于伯努利模型的朴素贝叶斯算法：
1 from numpy import * 2 3 def loadDataSet(): 4 ‘‘‘ 5 创建词条数据集 6 :return:单词列表postingList,所属类别classVec 7 ‘‘‘ 8 postingList=[[‘my‘, ‘dog‘, ‘has‘, ‘flea‘, ‘problems‘, ‘help‘, ‘please‘], 9 [‘maybe‘, ‘not‘, ‘take‘, ‘him‘, ‘to‘, ‘dog‘, ‘park‘, ‘stupid‘], 10 [‘my‘, ‘dalmation‘, ‘is‘, ‘so‘, ‘cute‘, ‘I‘, ‘love‘, ‘him‘], 11 [‘stop‘, ‘posting‘, ‘stupid‘, ‘worthless‘, ‘garbage‘], 12 [‘mr‘, ‘licks‘, ‘ate‘, ‘my‘, ‘steak‘, ‘how‘, ‘to‘, ‘stop‘, ‘him‘], 13 [‘quit‘, ‘buying‘, ‘worthless‘, ‘dog‘, ‘food‘, ‘stupid‘]] 14 # 1代表侮辱性词条，0代表正常词条 15 classVec = [0, 1, 0, 1, 0, 1] 16 return postingList, classVec 17 18 def createVocabList(dataSet): 19 ‘‘‘ 20 获取所有单词的集合 21 :param dataSet:数据集 22 :return:所有单词的集合（不包含重复单词的列表） 23 ‘‘‘ 24 vocabSet = set() 25 for document in dataSet: 26 # 操作符 | 用于求两个集合的并集 27 vocabSet = vocabSet | set(document) 28 return list(vocabSet) 29 30 def setOfWords2Vec(vocabList, inputSet): 31 ‘‘‘ 32 遍历查看该单词是否出现，出现该单词则将该单词置为1 33 :param vocabList:所有单词的集合列表 34 :param inputSet:输入数据集 35 :return:匹配列表[0,1,0,1,...]其中1与0表示词汇表中的单词是否出现在输入的数据集中 36 ‘‘‘ 37 returnVec = [0]*len(vocabList) 38 for word in inputSet: 39 if word in vocabList: 40 returnVec[vocabList.index(word)] = 1 41 else: 42 print("the word: %s is not in my vocabulary" % word) 43 return returnVec 44 45 def trainNB0(trainMatrix, trainCategory): 46 ‘‘‘ 47 :param trainMatrix:词条单词矩阵[[1,0,1,1,1....],[],[]...] 48 :param trainCategory:词条对应的类别[0,1,1,0....]，列表长度等于单词矩阵数，其中的1代表对应的词条是侮辱性词条，0代表不是侮辱性词条 49 :return: p0Vect:在类别0下，每个单词出现的概率；p1Vect:在类别1下，每个单词出现的概率；pAbusive:侮辱性词条出现的概率 50 ‘‘‘ 51 # 总词条数 52 numTrainDocs = len(trainMatrix) 53 # 总单词数 54 numWords = len(trainMatrix[0]) 55 #侮辱性词条出现的概率，即trainCategory中所有的1的个数除以总词条数（本训练集为0.5） 56 pAbusive = sum(trainCategory)/float(numTrainDocs) 57 # 构造单词出现次数列表 58 # p0Num 各个单词在正常词条中出现的次数 59 # p1Num 各个单词在侮辱性词条中出现的次数 60 p0Num = ones(numWords) 61 p1Num = ones(numWords) 62 63 # p0Denom 词条数据集中正常词条中单词总量 64 # p1Denom 词条数据集中侮辱性词条中单词总量 65 p0Denom = 2.0 66 p1Denom = 2.0 67 for i in range(numTrainDocs): 68 # 判断是否是侮辱性词条 69 if trainCategory[i] == 1: 70 # 如果是侮辱性词条，对污辱性文件的向量进行加和 71 #print(trainMatrix[i], "污辱性词条") 72 p1Num += trainMatrix[i] 73 #print(p1Num, "各个单词在侮辱性词条中出现的次数") 74 # 对向量中的所有元素进行求和，也就是计算所有侮辱性文件中出现的单词总数 75 p1Denom += sum(trainMatrix[i]) 76 #print(p1Denom, "侮辱性词条单词总数") 77 else: 78 #print(trainMatrix[i], "正常词条") 79 p0Num += trainMatrix[i] 80 #print(p0Num, "各个单词在正常词条中出现的次数") 81 p0Denom += sum(trainMatrix[i]) 82 #print(p0Denom, "正常词条单词总数") 83 # 类别1，即侮辱性词条的[P(w1|c1),P(w2|c1),P(w3|c1),P(w4|c1),P(w5|c1)....]列表 84 p1Vect = log(p1Num / p1Denom) # 用log函数防止下溢出 85 # 类别0，即正常词条的[P(w1|c0),P(w2|c0),P(w3|c0),P(w4|c0),P(w5|c0)....]列表 86 p0Vect = log(p0Num / p0Denom) 87 return p0Vect, p1Vect, pAbusive 88 89 def classifyNB(vec_to_Classify, p0Vect, p1Vect, pAbusive): 90 ‘‘‘ 91 使用算法： 92 # 将乘法转换为加法 93 乘法：P(c|w1,w2,...,wn) = P(w1,w2,...,wn|c)P(c)/P(w1,w2,...,wn) 94 加法：P(w1|c)*P(w2|c)....P(wn|c)P(c) -> log(P(w1|c))+log(P(w2|c))+....+log(P(wn|c))+log(P(c)) 95 注意：对于每个类别c，p(w)即p(w1,w2,...,wn)都是相同的,故只需比较分子的大小。 96 :param vec_to_Classify:待分类的词条 97 :param p0Vect:类别0，即各单词出现在正常词条下的概率列表[P(w1|c1),P(w2|c1),P(w3|c1),P(w4|c1),P(w5|c1)....] 98 :param p1Vect:类别1，即各单词出现在侮辱性词条下的概率列表[P(w1|c0),P(w2|c0),P(w3|c0),P(w4|c0),P(w5|c0)....] 99 :param pAbusive:类别1，侮辱性词条出现的概率 100 :return: 101 ‘‘‘ 102 # 公式（vec_to_Classify * p1Vect）是为了计算该词条中的各个单词出现在正常或侮辱性词条下的概率 103 p1 = sum(vec_to_Classify * p1Vect) + log(pAbusive) 104 p0 = sum(vec_to_Classify * p0Vect) + log(1.0 - pAbusive) 105 if p1 > p0: 106 return 1 107 else: 108 return 0 109 110 def testingNB(): 111 # 加载数据集，文件分类列表 112 dataSet, classVec = loadDataSet() 113 # 创建全部单词集合列表（非重复） 114 vocabList = createVocabList(dataSet) 115 # 计算每个文件里的单词是否在vocaList中出现，并创建文件单词矩阵 116 trainMatrix = [] 117 for dataDoc in dataSet: 118 trainMatrix.append(setOfWords2Vec(vocabList, dataDoc)) 119 # 训练数据 120 p0Vect, p1Vect, pAbusive = trainNB0(array(trainMatrix), array(classVec)) 121 testEntry = [‘love‘, ‘my‘, ‘dalmation‘] 122 thisDoc = array(setOfWords2Vec(vocabList, testEntry)) 123 print(‘词条‘, testEntry, ‘classified as: ‘, classifyNB(thisDoc, p0Vect, p1Vect, pAbusive)) 124 125 if __name__ == ‘__main__‘: 126 testingNB()
标签：并集 规则 假设 创建 white 乘法 mamicode document may
原文地址：https://www.cnblogs.com/lovewhale1997/p/11252066.html
