标签:理解 直接 引入 man 规划 algorithm pre 偶数 star
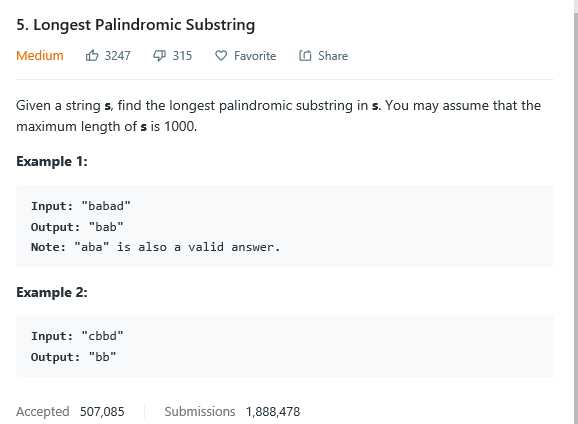
解法一:中心拓展法。从下标为0开始遍历,将每个元素当作回文串中心,向两边拓展。
1)以这个字符为中心的回文串的长度(奇数串);
2)以这个字符和下个字符为中心的回文串的长度(偶数串)。
注意:既要统计回文串为奇数时,又要统计回文串为偶数时。当 s[left]!=s[right] 时,left多减了1,right多加了1,所以在计算回文串开头时要把left+1,长度要是(right-1)-(left+1)-1 = right - left -1
class Solution {
public:
string longestPalindrome(string s) {
int len = s.size();
int maxlen = 1;
int start = 0;
//aba
for(int i=0; i<len; i++){
int j = i-1;
int k = i+1;
while(j>=0 && k<len && s[j]==s[k]){
if(k-j+1 > maxlen){
maxlen = k-j+1;
start = j;
}
j--;
k++;
}
}
//abba
for(int i=0; i<len; i++){
int j = i;
int k = i+1;
while(j>=0 && k<len && s[j]==s[k]){
if(k-j+1 > maxlen){
maxlen = k-j+1;
start = j;
}
j--;
k++;
}
}
return s.substr(start, maxlen);
}
};
class Solution {
public:
string longestPalindrome(string s) {
//这个写法更简便
if(s.size() <2 )
return s;
int maxlen = 0, start=0;
for(int i=0; i<s.size()-1; ++i){
palind(s,i,i,start, maxlen);
palind(s, i, i+1, start, maxlen);
}
return s.substr(start, maxlen);
}
void palind(string s, int left, int right, int& start, int& maxlen){
while(left>=0 && right<s.size() && s[left]==s[right]){
right++;
left--;
}
if(maxlen < right-left-1){
start = left+1;
maxlen = right - left -1;
}
}
};
class Solution {
public:
string longestPalindrome(string s) {
int len = s.size();
if(len==0 || len==1)
return s;
string s1="", s2="", p="";
for(int k=0; k<len; ++k){
//这里 k<len 或 k<len-1 都可以
s1 = palind(s, k, k);
if(s1.size() > p.size())
p = s1;
s2 = palind(s, k, k+1);
if(s2.size() > p.size())
p = s2;
}
return p;
}
string palind(string s, int i, int j){
//以i和j为两端的回文串长度
while(i>=0 && j<s.size() && s[i] == s[j] ){
i--;
j++;
}
return s.substr(i+1, j-i-1);
}
};
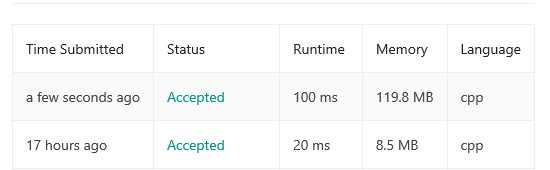
我把重复的代码写成一个函数调用之后 更慢了==
解法二:Manacher Algorithm(马拉车算法)是解决在一个字符串中寻找最长回文串的O(n)算法。实在是不好理解。
参考视频:https://www.youtube.com/watch?v=SV1ZaKCozS4
参考链接:https://zhuanlan.zhihu.com/p/62351445?utm_source=wechat_session&utm_medium=social&utm_oi=544807589276360704
思路:
1. 调整字符串
因为回文子串有两种可能"aba"和"bb",如果直接处理需要判断子串中心是否有字符。而马拉车算法先为字符串填充无效字符,例如"#"。这样上述字符串就变成"#a#b#a#"和"#b#b#"。这样无论原字符串怎样,新生成的字符串都是长度为奇数,中心有字符。
2. 判断字符半径
这里先引入一些概念和变量。
字符半径:就是以该字符为中心可以形成的最大回文字符串的半径。比如"#a#b#a#"的半径为3。
节点 i :被遍历节点i。
节点maxR : 容纳节点i最大回文子串所覆盖的最大位置。
节点pos : 容纳节点i最大回文子串的中心位置。
节点j : 以pos为中心,节点i的对称位置。
数组R : 记录所有节点为中心的最大回文半径,如"#a#b#a#" R[3] 的最大回文半径为4,要在字符半径的基础上加上本身的长度1 。
之后节点i从左至右遍历字符串,首先预估节点i最小半径,不断扩大搜索范围以确定最终半径。数组R记录下来。最终有了全部回文子串的中心和半径就能确定算法就可以解决。
3. 如何确定节点i的最小半径
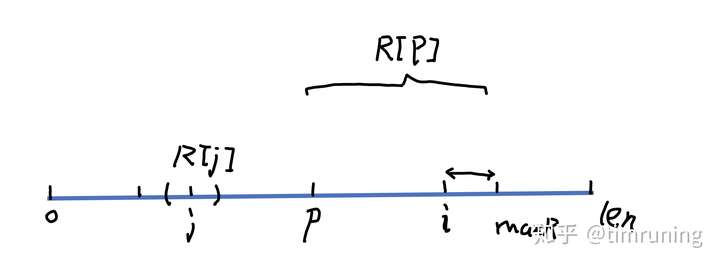
如果所有节点i的半径都从0开始枚举,算法复杂度太高。因为在遍历节点i之前,数组R已经记录了过去节点的回文信息。通过maxR和pos记录容纳节点i最大回文子串信息。因为回文子串的左右必然对称,可以估计节点i的半径最小在maxR-i 和其对称节点 j = pos*2 -1 半径之间。如图:
公式:
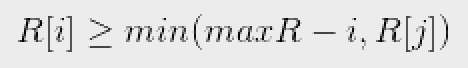
当节点i探索范围超过maxR,则替换maxR和pos。以此遍历完整个字符串后,选择最大子串,保留在奇数位原字符串字符即可。
class Solution { public: string manacher(string& x){ string a = "#"; for(char v : x){ a.push_back(v); a.append("#"); // #c#b#b#d# #b#a#b#a#d# } int pos = 0; //容纳节点i最大回文子串的中心位置 int maxR = 0; //容纳节点i最大回文子串所覆盖的最大位置 // R 记录所有节点为中心的最大回文串的半径 vector<int> R(a.size(), 0); for(int i=0; i<a.size(); ++i){ // 2*pos-i = mirror(i) //节点i未超过最大回文串的边界时,取min(mirror[i], 最大回文串的边界),否则为0 R[i] = maxR>i ? min(maxR-i, R[2*pos-i]) : 0; //从i+R[i] 和 i-R[i]之外开始遍历看是否相同 while(R[i]+i<a.size() && i>=R[i] && a[i-R[i]] == a[i+R[i]]) R[i]++; if(R[i] + i > maxR){ maxR = R[i]+i; pos = i; } } int sub[] = {0, 0}; //sub储存{回文串中心,半径长度} for(int i=0; i<a.size(); ++i){ if(R[i] > sub[1]){ sub[0] = i; sub[1] = R[i]; } } string sub2 = ""; for(int i=sub[0]-sub[1]+1; i<=sub[0]+sub[1]-1; ++i){ if(i%2 == 1) //取奇数位 sub2 += a[i]; } return sub2; } string longestPalindrome(string s) { return manacher(s); } };
(Manacher Algorithm, 中心拓展法,动态规划) leetcode 5. 最长回文串
标签:理解 直接 引入 man 规划 algorithm pre 偶数 star
原文地址:https://www.cnblogs.com/Bella2017/p/11258444.html