标签:algorithm 机房 src 测试数据 nbsp sizeof bre opened org
2020年,人类在火星上建立了一个庞大的基地群,总共有n个基地。起初为了节约材料,人类只修建了n-1条道路来连接这些基地,并且每两个基地都能够通过道路到达,所以所有的基地形成了一个巨大的树状结构。如果基地A到基地B至少要经过d条道路的话,我们称基地A到基地B的距离为d。
由于火星上非常干燥,经常引发火灾,人类决定在火星上修建若干个消防局。消防局只能修建在基地里,每个消防局有能力扑灭与它距离不超过2的基地的火灾。
你的任务是计算至少要修建多少个消防局才能够确保火星上所有的基地在发生火灾时,消防队有能力及时扑灭火灾。
输入文件名为input.txt。
输入文件的第一行为n (n<=1000),表示火星上基地的数目。接下来的n-1行每行有一个正整数,其中文件第i行的正整数为a[i],表示从编号为i的基地到编号为a[i]的基地之间有一条道路,为了更加简洁的描述树状结构的基地群,有a[i]<i。
输出文件名为output.txt
输出文件仅有一个正整数,表示至少要设立多少个消防局才有能力及时扑灭任何基地发生的火灾。
6 1 2 3 4 5
2
这题是一道树形DP。
但是,rt,我们贪心。
每一道题都有自己独特的性质,如果这条性质能被我们所利用,那么就可以简化问题。
首先,观察题目,我们发现这样的一句话:
每个消防局有能力扑灭与它距离不超过2的基地的火灾。
似乎不太直观?
那画个图吧。
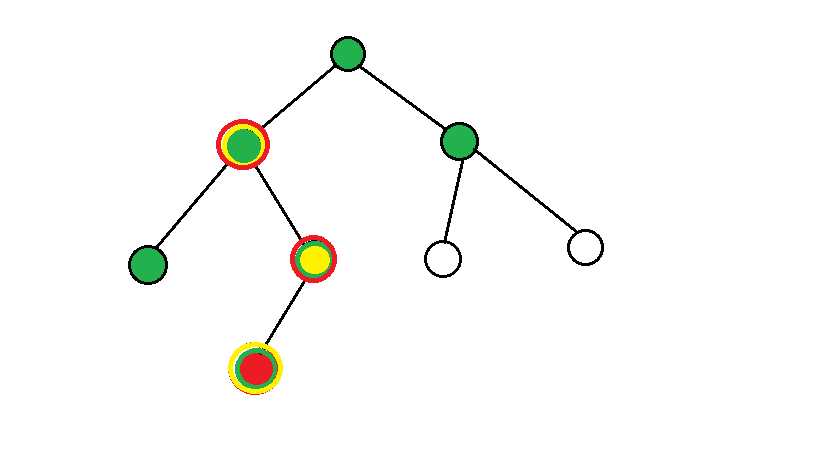
我们发现,对于一个节点【深度最深的红点,来说,能够覆盖他的,只有四种:
1.自己
2.爸爸
3.兄弟
4.爷爷
但是我们观察上图,发现:
该点的爷爷其实是包含但不只包含其子孙能产生的覆盖范围。
也就是说,爷爷是最优的。
那么我们就可以依次把深度最深的节点的爷爷找出来,在那里建立消防站。
ok,结束了。

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 #include<queue> 7 using namespace std; 8 9 const int MA=1010; 10 int n,ecnt,ans; 11 int f[MA],head[MA],s[MA],dept[MA]; 12 bool vis[MA]; 13 struct ss{ 14 int to,nxt; 15 }t[MA*2]; 16 priority_queue< pair<int,int> > q; 17 18 inline void add(int a,int b) { 19 t[++ecnt].nxt=head[a]; 20 t[ecnt].to=b; 21 head[a]=ecnt; 22 return; 23 } 24 25 inline int read() { 26 int x=0;char ch=getchar(); 27 while(ch<‘0‘||ch>‘9‘)ch=getchar(); 28 while(ch>=‘0‘&&ch<=‘9‘)x=(x<<3)+(x<<1)+ch-‘0‘,ch=getchar(); 29 return x; 30 } 31 32 void dfs1(int x,int fa) { 33 vis[x]=1; 34 dept[x]=dept[fa]+1; 35 q.push(make_pair(dept[x],x)); 36 for(int i=head[x];i;i=t[i].nxt) { 37 int y=t[i].to; 38 if(!vis[y]) dfs1(y,x); 39 } 40 } 41 42 void dfs2(int x,int d) { 43 if(d>2) return; 44 vis[x]=1; 45 for(int i=head[x];i;i=t[i].nxt) dfs2(t[i].to,d+1); 46 } 47 48 int main() 49 { 50 n=read(); 51 f[1]=1; 52 for(int i=2;i<=n;i++) { 53 f[i]=read(); 54 add(i,f[i]); 55 add(f[i],i); 56 } 57 dfs1(1,1); 58 memset(vis,0,sizeof vis); 59 while(!q.empty()) { 60 while(!q.empty()&&vis[q.top().second]) q.pop(); 61 if(q.empty()) break; 62 int t=q.top().second; 63 q.pop(); 64 dfs2(f[f[t]],0); 65 ans++; 66 } 67 printf("%d",ans); 68 return 0; 69 }
pdf题面和大样例链接:http://pan.baidu.com/s/1cawM7c 密码:xgxv
历史/落在/赢家/之手
至少/我们/拥有/传说
谁说/败者/无法/不朽
拳头/只能/让人/低头
念头/却能/让人/抬头
抬头/去看/去爱/去追
你心中的梦
又想起了四月。
如果不是省选,大家大概不会这么轻易地分道扬镳吧? 只见一个又一个昔日的队友离开了机房。
凭君莫话封侯事,一将功成万骨枯。
梦里,小 F 成了一个给将军送密信的信使。
现在,有两封关乎国家生死的密信需要送到前线大将军帐下,路途凶险,时间紧迫。小 F 不因为自己的祸福而避趋之,勇敢地承担了这个任务。
不过,小 F 实在是太粗心了,他一不小心把两封密信中的一封给弄掉了。
小 F 偷偷打开了剩下的那封密信。他 发现一副十分详细的地图,以及几句批文——原来 这是战场周围的情报地图。他仔细看后发现,在这张地图上标记了 n 个从 1 到 n 标号的 驿站,n − 1 条长度为 1 里的小道,每条小道双向连接两个不同的驿站,并且驿站之间可以 通过小道两两可达。
小 F 仔细辨认着上面的批注,突然明白了丢失的信的内容了。原来,每个驿站都可以驻 扎一个小队,每个小队可以控制距离不超过 k 里的驿站。如果有驿站没被控制,就容易产 生危险——因此这种情况应该完全避免。而那封丢失的密信里,就装着朝廷数学重臣留下的 精妙的排布方案,也就是用了最少的小队来控制所有驿站。
小 F 知道,如果能计算出最优方案的话,也许他就能够将功赎过,免于死罪。他找到了 你,你能帮帮他吗? 当然,小 F 在等待你的支援的过程中,也许已经从图上观察出了一些可能会比较有用的 性质,他会通过一种特殊的方式告诉你。
从标准输入中读入数据。
输入第 1 行一个正整数 n,k,t,代表驿站数,一支小队能够控制的最远距离,以及特 殊性质所代表的编号。关于特殊性质请参照数据范围。
输入第 2 行至第 n 行,每行两个正整数 u_iui?,v_ivi?,表示在 u_iui? 和 v_ivi? 间,有一条长度为 一里的小道。
输出到标准输出中。
输出一行,为最优方案下需要的小队数。
4 1 0 1 2 1 3 1 4
1
6 1 0 1 2 1 3 1 4 4 5 4 6
2
【样例 1 说明】
如图。由于一号节点到周围的点距离均是 1,因此可以控制所有驿站。
【样例 2 说明】
如图,和样例 1 类似。
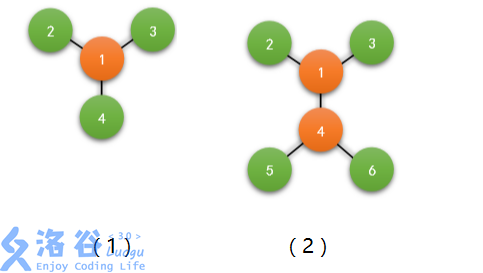
子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难,可以尝试只解 决一部分测试数据。
关于 t 的含义如下: t = 0:该测试点没有额外的特殊性质; t = 1:保证最多 8 个点的所连接的小道超过 1 条; t = 2:保证所有点到 1 号点的距离不超过 2。
每个测试点的数据规模及特点如下表
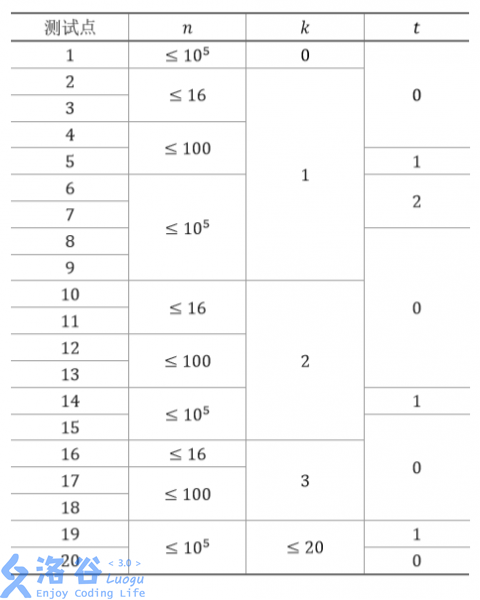
这题跟上面那个其实很像。
我们观察到题目中有这样一句话:
每个小队可以控制距离不超过 k 里的驿站。如果有驿站没被控制,就容易产 生危险——因此这种情况应该完全避免
好了,这两题基本一样了。
接下来只要再写一遍上面的代码,修改一下就好了。
我的代码没有修改,加了个玄学优化,不具有泛用性,就不放上来了QAQ
需要可以私信。
标签:algorithm 机房 src 测试数据 nbsp sizeof bre opened org
原文地址:https://www.cnblogs.com/qxyzili--24/p/11259039.html