标签:mes turn long ret ble bre else 前缀和 new
推推式子就好了
首先把题目要求的式子写出来:
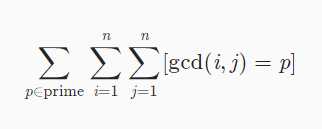
把里面的p除掉:
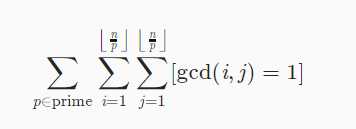
把枚举j的上界改为i,因为(i,j),(j,i)我们一次就可以算出,而-1是因为i=j时多算了一次。
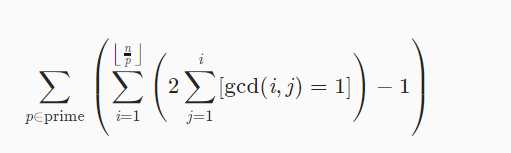
把里面的项改写为φ(i),得:
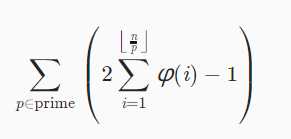
所以只需要线性筛时求出φ(i),然后再求个前缀和就行。
1 #include<bits/stdc++.h> 2 #define INTMAX 2147483647LL 3 #define PII pair<int,int> 4 #define MK make_pair 5 #define re register 6 using namespace std; 7 typedef long long ll; 8 const double Pi=acos(-1.0); 9 const int Inf=0x3f3f3f3f; 10 const int MAXN=1e7+10; 11 inline int read(){ 12 re int x=0,f=1,ch=getchar(); 13 while(!isdigit(ch))f=ch==‘-‘?-1:1,ch=getchar(); 14 while(isdigit(ch))x=x*10+ch-48,ch=getchar(); 15 return x*f; 16 } 17 inline ll readll(){ 18 re ll x=0,f=1,ch=getchar(); 19 while(!isdigit(ch))f=ch==‘-‘?-1:1,ch=getchar(); 20 while(isdigit(ch))x=x*10+ch-48,ch=getchar(); 21 return x*f; 22 } 23 24 25 int n,tot; 26 int p[MAXN],phi[MAXN]; 27 bool vis[MAXN]; 28 ll sum[MAXN]; 29 inline void Sieve(){ 30 phi[1]=1; 31 for(int i=2;i<=n;++i){ 32 if(!vis[i]) p[++tot]=i,phi[i]=i-1; 33 for(int j=1;j<=tot&&i*p[j]<=n;++j){ 34 vis[i*p[j]]=1; 35 phi[i*p[j]]=phi[i]*p[j]; 36 if(i%p[j]==0){ 37 phi[i*p[j]]=phi[i]*p[j]; 38 break; 39 } 40 else 41 phi[i*p[j]]=phi[i]*phi[p[j]]; 42 } 43 } 44 for(int i=1;i<=n;++i) 45 sum[i]=sum[i-1]+phi[i]; 46 } 47 int main(){ 48 n=read(); 49 Sieve(); 50 ll ans=0; 51 for(int i=1;i<=tot;++i) 52 ans+=2*sum[n/p[i]]-1; 53 printf("%lld\n",ans); 54 return 0; 55 }
标签:mes turn long ret ble bre else 前缀和 new
原文地址:https://www.cnblogs.com/LI-dox/p/11261583.html