51Nod1120 机器人走方格 V3

标签：一个   关于   big   代码   51nod   mod   题目   bit   turn   

题目

N * N的方格，从左上到右下画一条线。一个机器人从左上走到右下，只能向右或向下走。并要求只能在这条线的上面或下面走，不能穿越这条线，有多少种不同的走法？由于方法数量可能很大，只需要输出Mod 10007的结果。
N<=1e9

思路

卡特兰数+卢卡斯定理+乘法逆元算组合数

卡特兰数：某百科卡特兰数词条讲过这种情况。

卢卡斯定理：组合数，模数很小，逐次拆分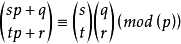

乘法逆元，见前面，此处n+1不能保证和p互质，建议用卡特兰数两组合数相减的公式。（不过数据很弱我写的/(n+1)）

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define db double
#define mod 10007
ll n;
ll gcd(ll a,ll b){
    return b==0?a:gcd(b,a%b);
}
ll speed(ll a,ll b,ll p){
    ll cur=a,ans=1;
    while(b){
        if(b&1) ans=ans*cur%p;
        cur=cur*cur%p;
        b>>=1;
    }
    return ans%p;
}
ll inv(ll t,ll p) {//Inverse element,求t关于p的逆元,注意:t要小于p,最好传参前先把t%p一下 
    return t==1?1:(p-p/t)*inv(p%t,p)%p;
}
ll Scomb(ll _n,ll _m,ll p){//SmallCombination n,m可以线性求出 
    if(_m==0) return 1;
    //return Factorial(_n,p)*inv(Factorial(m,p)%p,p)%p*inv(Factorial(n-m,p)%p,p)%p;
    ll ans=1,tmp=1;
    for(ll i=_m+1;i<=_n;i++){
        ans=(ans*i)%p;
    }
    for(ll i=1;i<=_n-_m;i++){
        tmp=(tmp*i)%p;
    }
    //cout<<tmp<<endl;
    return ans*inv(tmp%p,p)%p;
}
ll Bcomb(ll _n,ll _m,ll p){//BigCombination
    if(_n<p&&_m<p) return Scomb(_n,_m,p)%p;
    return Bcomb(_n/p,_m/p,p)*Scomb(_n%p,_m%p,p)%p;
}

int main(){
    cin>>n;
    n--;
    ll ans=2*Bcomb(2*n,n,mod)*speed(n+1,mod-2,mod)%mod;
    cout<<ans<<endl;
    //cout<<speed(2,mod-2,mod)%mod;
    return 0;
}

51Nod1120 机器人走方格 V3

标签：一个   关于   big   代码   51nod   mod   题目   bit   turn   

原文地址：https://www.cnblogs.com/sz-wcc/p/11267035.html