标签:mamicode order ++ btree out map scan printf def
一棵BST如下
插入顺序: 1, 11, 12, 17, 20, 5, 8, 15
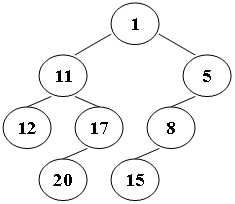
不难知道:
1、LCA(a, b) 属于 [a, b]
2.、如果a, b的公共祖先是a||b,那么我们可以知道,先出现的结点一定在上面,后出现的结点一定在下面,初始序列中a,b先出现的那个就是公共祖先。
3、如果a, b的公共祖先是c, 那么我们只需要找序列中值位于a,b之间的第一次出现的元素即可, 比如20和15的公共祖先就是1,因为1是所有位于15和20之间的值中最早出现的。
例题:https://pintia.cn/problem-sets/994805342720868352/problems/994805343727501312
The lowest common ancestor (LCA) of two nodes U and V in a tree is the deepest node that has both U and V as descendants. A binary search tree (BST) is recursively defined as a binary tree which has the following properties: The left subtree of a node contains only nodes with keys less than the node‘s key. The right subtree of a node contains only nodes with keys greater than or equal to the node‘s key. Both the left and right subtrees must also be binary search trees. Given any two nodes in a BST, you are supposed to find their LCA. Input Specification: Each input file contains one test case. For each case, the first line gives two positive integers: M (≤ 1,000), the number of pairs of nodes to be tested; and N (≤ 10,000), the number of keys in the BST, respectively. In the second line, N distinct integers are given as the preorder traversal sequence of the BST. Then M lines follow, each contains a pair of integer keys U and V. All the keys are in the range of int. Output Specification: For each given pair of U and V, print in a line LCA of U and V is A. if the LCA is found and A is the key. But if A is one of U and V, print X is an ancestor of Y. where X is A and Y is the other node. If U or V is not found in the BST, print in a line ERROR: U is not found. or ERROR: V is not found. or ERROR: U and V are not found.. Sample Input: 6 8 6 3 1 2 5 4 8 7 2 5 8 7 1 9 12 -3 0 8 99 99 Sample Output: LCA of 2 and 5 is 3. 8 is an ancestor of 7. ERROR: 9 is not found. ERROR: 12 and -3 are not found. ERROR: 0 is not found. ERROR: 99 and 99 are not found.
AC代码:(利用BBST求解BST的LCA问题)
1 #include <iostream> 2 #include <vector> 3 #include <map> 4 using namespace std; 5 map<int, bool> mp; 6 int main() { 7 int m, n, u, v, a; 8 scanf("%d %d", &m, &n); 9 vector<int> pre(n); 10 for (int i = 0; i < n; i++) { 11 scanf("%d", &pre[i]); 12 mp[pre[i]] = true; 13 } 14 for (int i = 0; i < m; i++) { 15 scanf("%d %d", &u, &v); 16 for(int j = 0; j < n; j++) { 17 a = pre[j]; 18 if ((a >= u && a <= v) || (a >= v && a <= u)) break; 19 } 20 if (mp[u] == false && mp[v] == false) 21 printf("ERROR: %d and %d are not found.\n", u, v); 22 else if (mp[u] == false || mp[v] == false) 23 printf("ERROR: %d is not found.\n", mp[u] == false ? u : v); 24 else if (a == u || a == v) 25 printf("%d is an ancestor of %d.\n", a, a == u ? v : u); 26 else 27 printf("LCA of %d and %d is %d.\n", u, v, a); 28 } 29 return 0; 30 }
总结:处理一些具体的数据结构问题并非一定要从数据结构本身下手,可以利用一些数据结构的性质并使用其他算法有时候可以大幅度降低时间。
标签:mamicode order ++ btree out map scan printf def
原文地址:https://www.cnblogs.com/MasterYan576356467/p/11275456.html