标签:lca 构造 baidu lse 一个 ble 更新 == 知识
百度百科定义:“对于有根树T的两个结点u、v,最近公共祖先
表示一个结点x,满足x是u、v的祖先且x的深度尽可能大。”
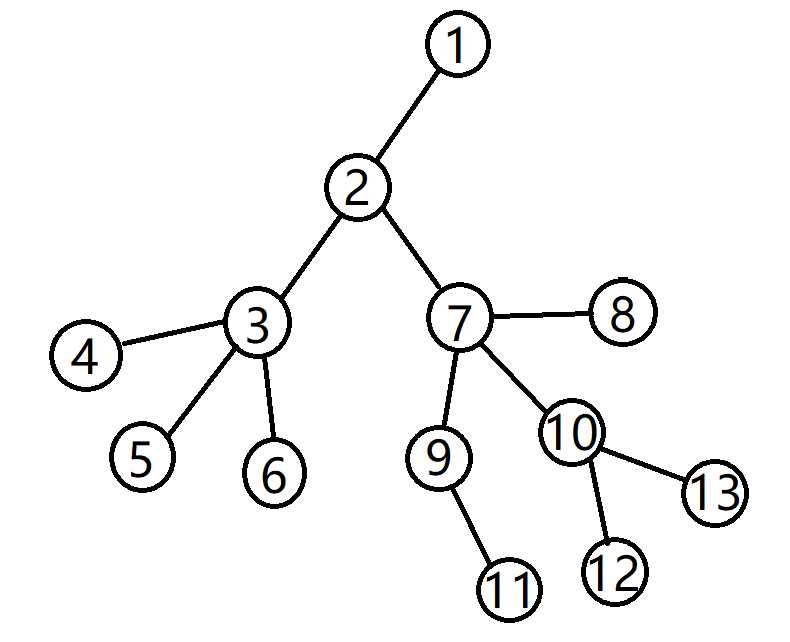
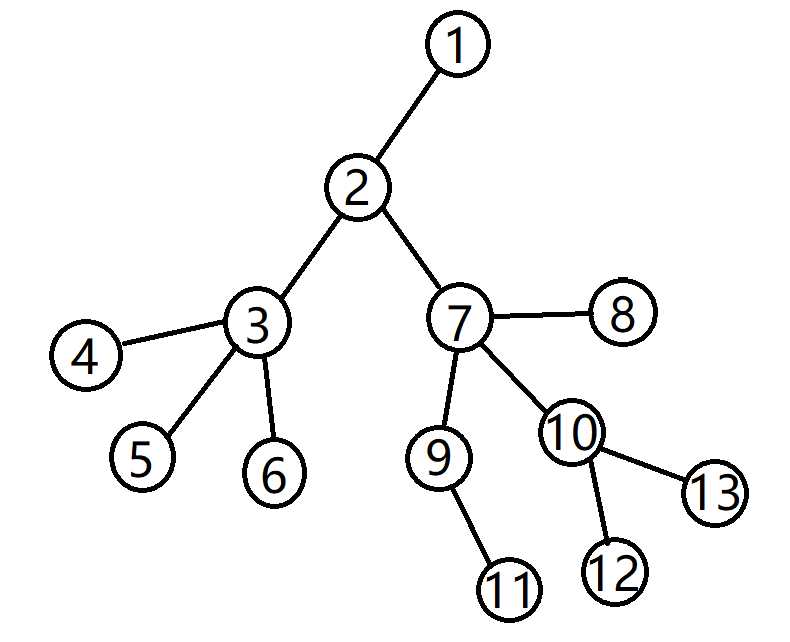
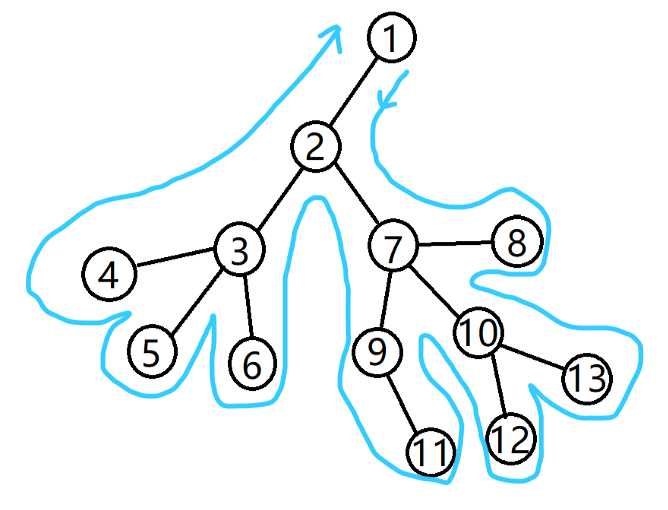
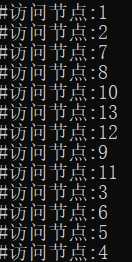
树上路径 实际访问路径
1 #include <iostream> 2 #include <cstdio>//标准输入输出 3 #include <cmath>//用于ST表中求解log 4 using namespace std; 5 int n,m,s,cnt,tot;// s:根节点,cnt:链式前向星,tot:总欧拉序列长度 6 int head[1000005];//链式前向星不解释 7 int depth[1000005];//记录当前结点深度 8 int num[1000005];//记录节点第一次出现位置 9 int rec[2000005][20];//查询数组 10 int st[2000005][20];//ST表结构数组 11 int euler[1000005];//欧拉序列数组 12 //int dp[1000005];求节点深度数组 13 //int wd[1000005];求某一深度树的宽度数组
1 struct edge 2 { 3 int nxt; 4 int to; 5 //int dis;边权值//在本示例中默认边权为1 6 }e[4000005];//建议开4倍数组 7 void add(int x,int y/*,int d*/) 8 { 9 e[++cnt].nxt=head[x]; 10 //e[cnt].dis=d; 11 e[cnt].to=y; 12 head[x]=cnt; 13 }
1 void dfs(int x,int dep)//x为当前节点,dep为当前节点深度 2 { 3 4 num[x]=++tot;//记录x节点第一次出现位置 5 depth[tot]=dep;//对应深度 6 euler[tot]=x;//记录序列 7 //dp[x]=max(dp[x],depth[tot]); //求某一结点深度 8 //cout<<"#访问节点:"<<x<<" depth数组:"<<depth[tot]<<endl; 9 for(int i=head[x];i;i=e[i].nxt)//遍历边 10 { 11 int p=e[i].to; 12 if(num[p]==0)//p节点如未出现 13 { 14 dfs(p,dep+1);//遍历 15 euler[++tot]=x;//回溯后记录序列 16 depth[tot]=dep;//记录对应深度 17 } 18 } 19 return ; 20 }
1 void RMQ(int N)//N:欧拉序列长度 2 { 3 for(int j=1;j<=(int)(log((double)N)/log(2.0));j++) 4 { 5 for(int i=1;i<=N;i++) 6 { 7 if(i+(1<<j)-1<=N) 8 if(st[i][j-1]<st[i+(1<<(j-1))][j-1])//同步更新rec[ ]数组 9 st[i][j]=st[i][j-1],rec[i][j]=rec[i][j-1]; 10 else 11 st[i][j]=st[i+(1<<(j-1))][j-1],rec[i][j]=rec[i+(1<<(j-1))][j-1]; 12 } 13 } 14 } 15 16 int search(int l,int r) 17 { 18 int k=(int)(log((double)(r-l+1))/log(2.0)); 19 if(st[l][k]<st[r-(1<<k)+1][k])//比较后返回rec[ ]数组对应节点编号 20 return rec[l][k]; 21 else 22 return rec[r-(1<<k)+1][k]; 23 }
1 int main() 2 { 3 cin>>n>>m>>s; 4 for(int i=1;i<=n-1;i++)//读边 5 { 6 int a,b; 7 scanf("%d %d",&a,&b); 8 add(a,b);//无向图正反存边 9 add(b,a); 10 } 11 dfs(s,1);//开始遍历 12 for(int i=1;i<=tot;i++)//初始化 13 { 14 st[i][0]=depth[i],rec[i][0]=euler[i]; 15 } 16 RMQ(tot);//构建ST表 17 /*//接下来是不必要部分//当初死在了这里 18 int dcnt=0,maxx=0;//dcnt:数的最大深度,maxx:数的最大宽度 19 for(int i=1;i<=n;i++) 20 { 21 wd[dp[i]]++;//统计所有深度为dp[i]的节点求出当前深度树宽度 22 } 23 for(int i=1;i<=n;i++) 24 { 25 if(wd[i]==0) 26 { 27 break; 28 } 29 dcnt++;//统计最大深度//笨方法 30 } 31 for(int i=1;i<=wcnt+1;i++) 32 { 33 maxx=max(maxx,wd[i]);//求最大宽度 34 } 35 36 */ 37 for(int i=1;i<=m;i++)//查询部分 38 { 39 int l,r,fg=0;//l:节点u,r:节点v,fg:交换标志 40 scanf("%d %d",&l,&r); 41 if(num[l]>num[r])//交换 42 { 43 swap(num[l],num[r]); 44 fg=1;//交换后标记 45 } 46 printf("%d\n",search(num[l],num[r]));//查询并输出 47 if(fg==1)//交换回来!!!!!记得交换回来!!!!!//p.s.2019/7/29模拟赛爆0 r.i.p 48 swap(num[l],num[r]); 49 } 50 return 0; 51 }
//暂时只想到这么多·········
标签:lca 构造 baidu lse 一个 ble 更新 == 知识
原文地址:https://www.cnblogs.com/randomaddress/p/11273861.html