动态规划入门(2):01背包问题

标签：max   i++   ora   题目   out   定义   col   names   include   

_____________________________________________________优秀的代码永垂不朽！

题目：

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

题目另述：有N件物品和一个容量为V的背包。放入第i件物品耗费的空间是C[i]，得到的价值是W[i]。求解将哪些物品装入背包可使价值总和最大。

基本思路：

这是最基础的背包问题，特点是:每种物品仅有一件，可以选择放或不放。

用子问题定义状态:即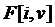表示前i件物品恰放入一个容量为v的背包可以获得的最大价值。则其状态转移方程便是：

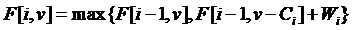
这个状态转移方程非常重要，基本上所有跟背包相关的问题的方程都是由它衍生出来的。

伪代码如下：

F[0,0...V]=0
for i = 1 to N
    for v=C[i] to V
        F[i,v]=max{F[i-1,v],F[i-1,v-C[i]+W[i]}
            

_______________________________________________________________________________________________________________________________________

转看正题:...

最裸的01背包，给你背包总量和物品数，以及物品的价值和体积，让你求背包装满后的最大价值

#include<bits/stdc++.h>
using namespace std;

const int N=1e3+10;
int w[N],v[N],dp[N];
int main()
{
    int T;cin>>T;
    while(T--){
    memset(dp,0,sizeof(dp));
    int N,V;cin>>N>>V;
    for(int i=1;i<=N;i++) cin>>v[i];
    for(int i=1;i<=N;i++) cin>>w[i];
    for(int i=1;i<=N;i++)
    {
        for(int j=V;j>=w[i];j--){
            dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
        }
    }
    cout<<dp[V]<<endl;
    }
    return 0;
}

牛刀可试：https://blog.csdn.net/nobleman__/article/details/78128318

参考：

《背包问题九讲》

________________________________________________________历经千重波浪，你是心之所向。

动态规划入门(2):01背包问题

标签：max   i++   ora   题目   out   定义   col   names   include   

原文地址：https://www.cnblogs.com/dragondragon/p/11275514.html