指数分布族

标签：分布   部分   log   statistic   stat   width   技术   说明   href   

指数族分布是一大类分布，基本形式为：

分布函数框架中的h(x),η(θ),T(x)和A(θ)并不是任意定义的，每一部分都有其特殊的意义。
θ是自然参数(natural parameter)，通常是一个实数；
h(x)是底层观测值（underlying measure）；
T(x)是充分统计量（sufficient statistic）；
A(θ)被称为对数规则化（log normalizer）。
---------------------

T(x)是x的充分统计量（能为相应分布提供足够信息的统计量）

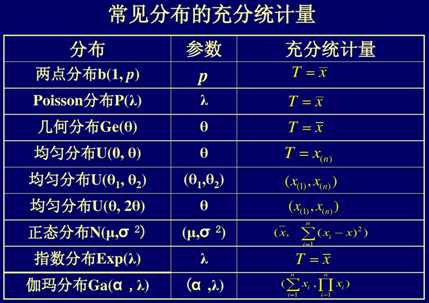
为了满足归一化条件，有：

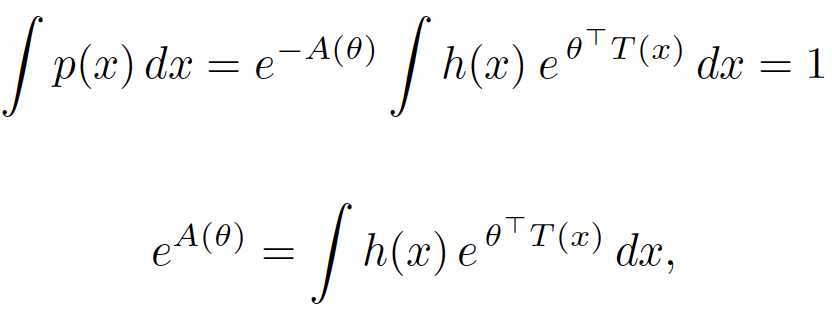
可以看出，当T(x)=x时，e^A(theta)是h(x)的拉普拉斯变换。

 指数族分布的例子：

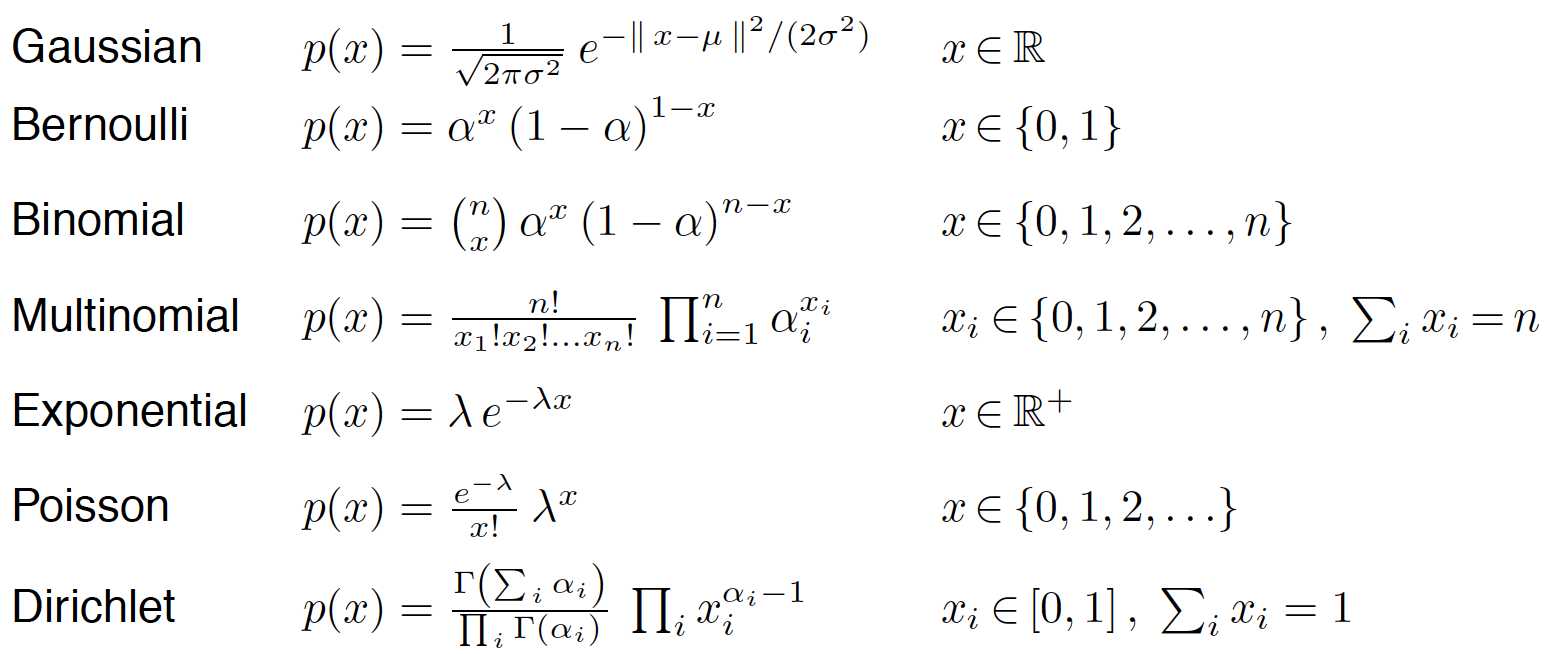
伯努利分布转换成指数族分布形式：

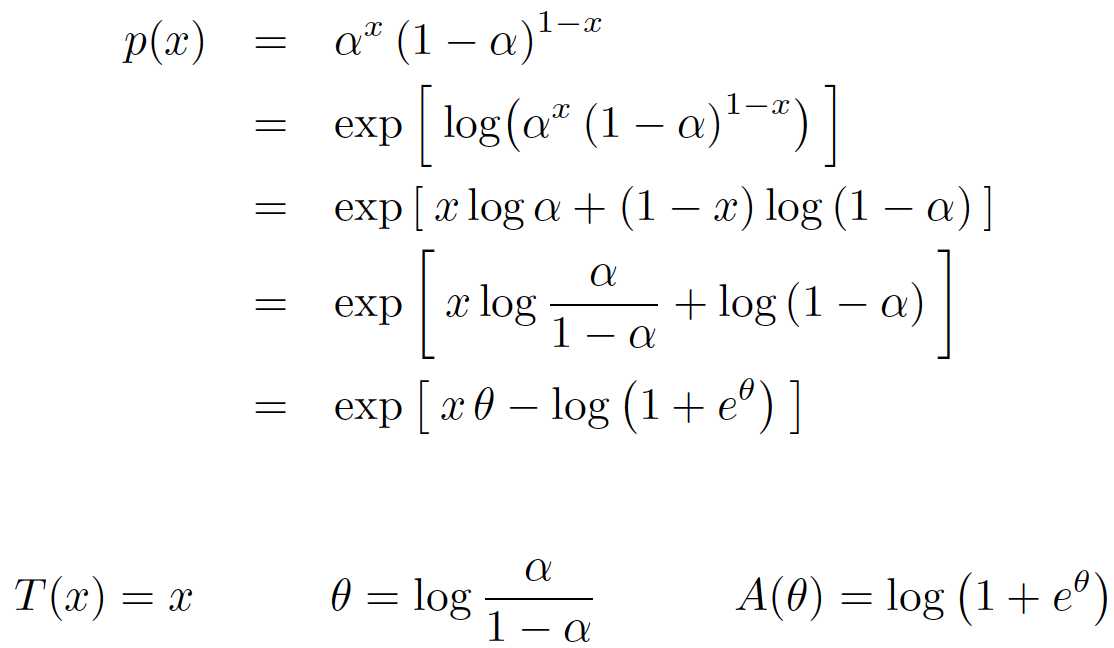
 单变量高斯分布的：

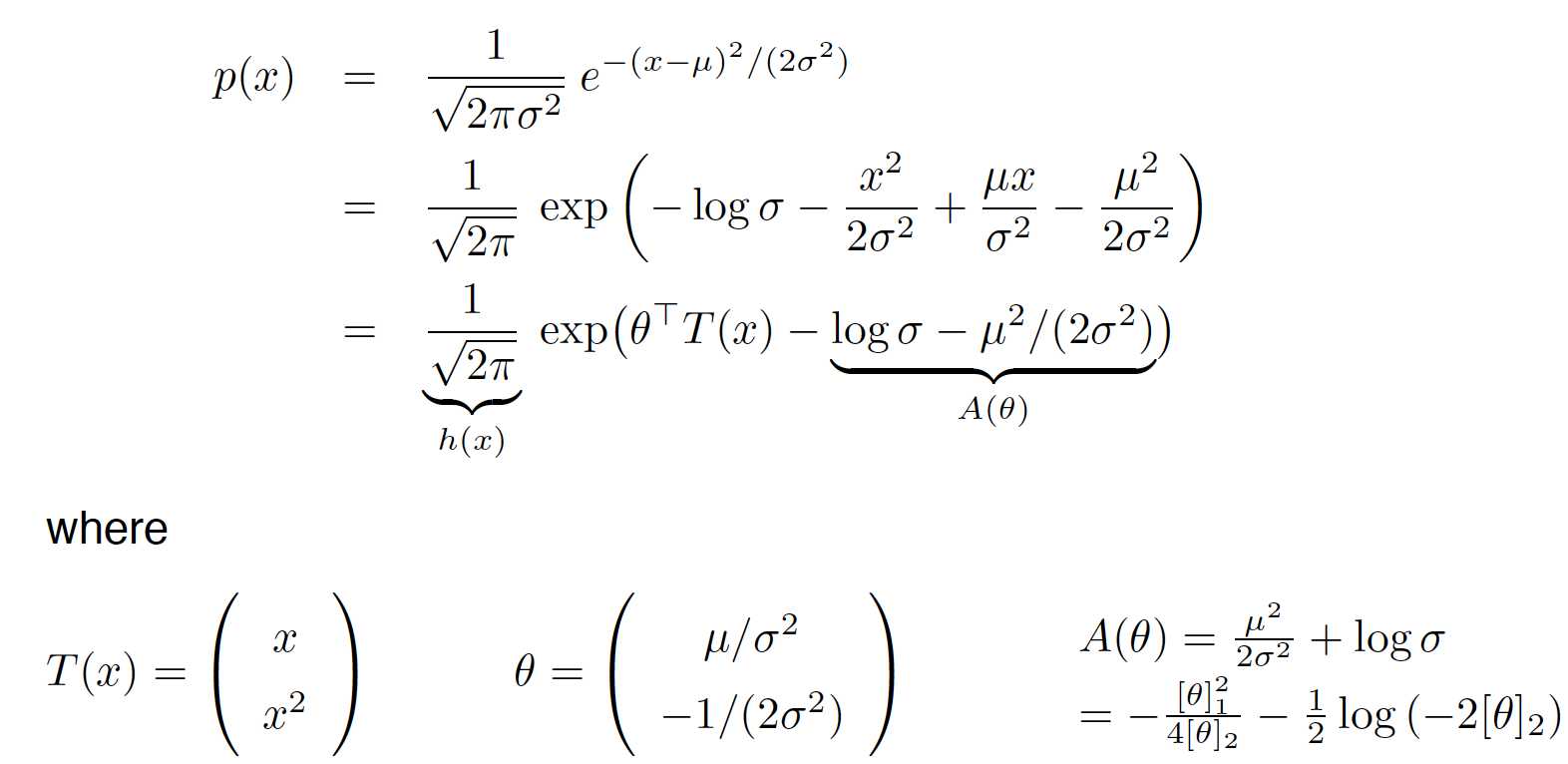
多变量高斯分布的：

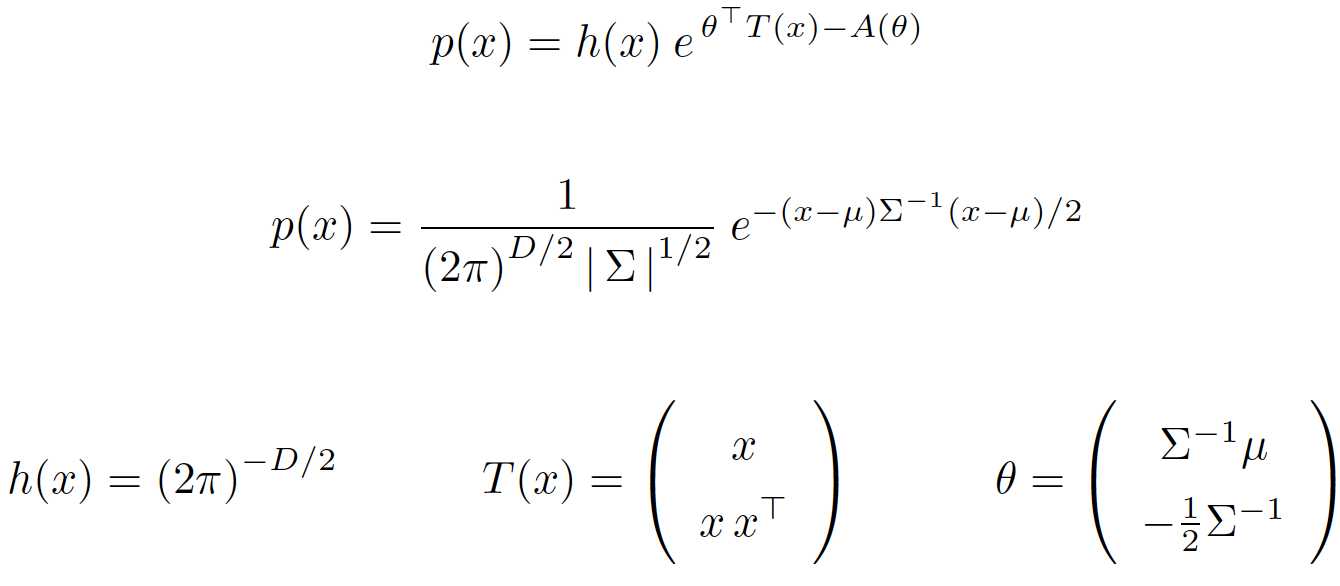
A（theta）的一阶导：

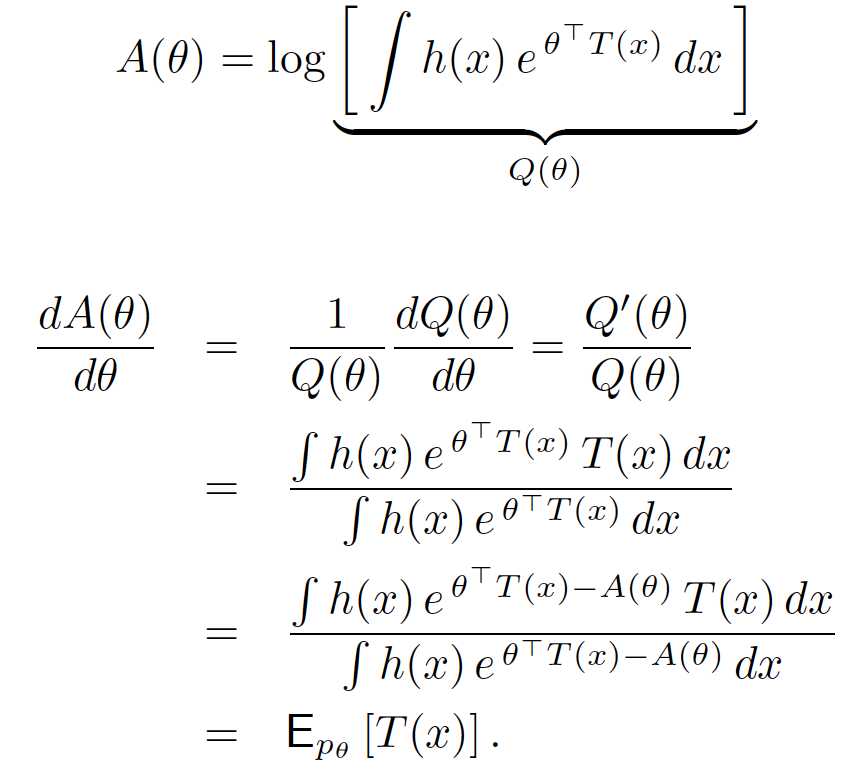
A（theta）的二阶导：

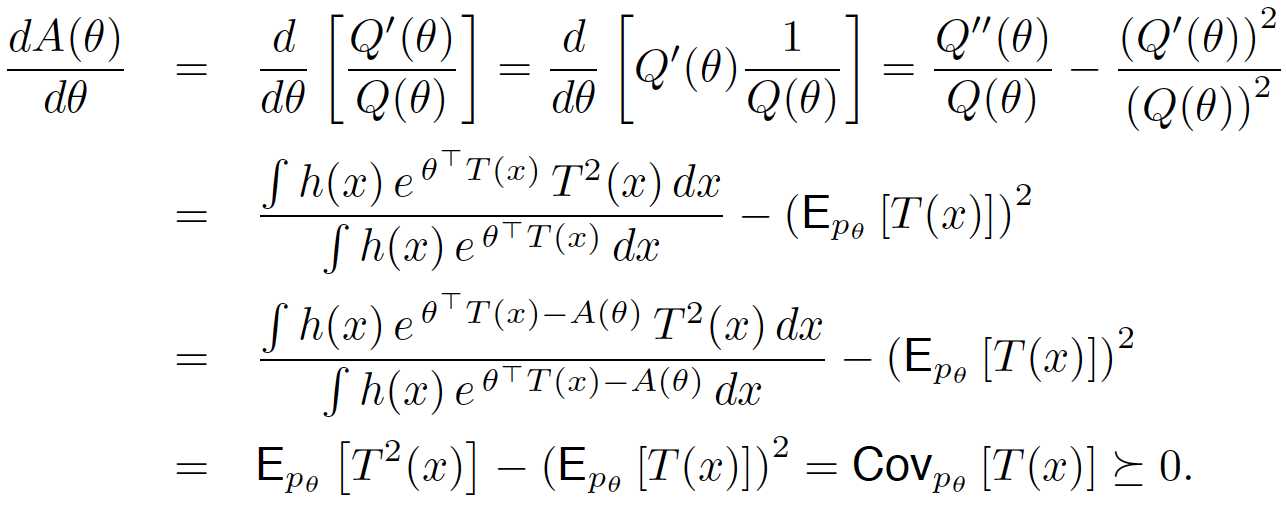
说明A（theta）是凸函数

计算log likehood，然后对theta求导，可得

而A的二次导时大于零的，所以A的一次导是增函数，上述方程最多只有一个解。

共轭先验：

似然估计：

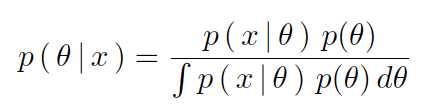
我们希望：

比如：

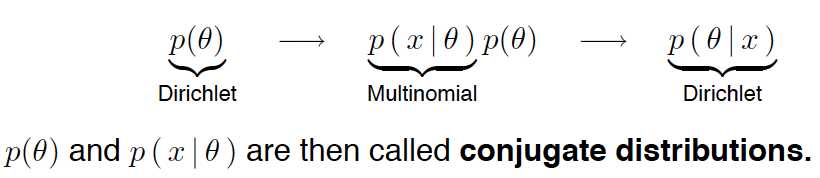
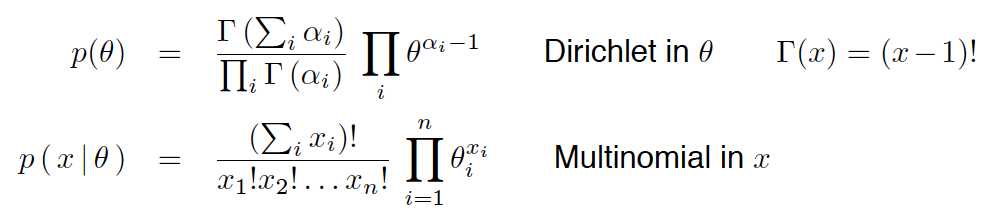
一些例子：

指数分布族

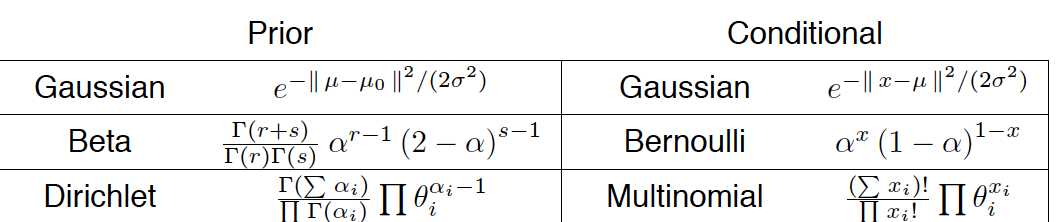
标签：分布   部分   log   statistic   stat   width   技术   说明   href   

原文地址：https://www.cnblogs.com/sddai/p/11279007.html