标签:alpha size mat new 抖动 nat round too real
? 使用 Ada Boosting 方法提升若干个弱分类器的效果
● 代码,每个感知机仅训练原数据集 trainRatio = 30% 的数据,然后进行调整和提升
1 import numpy as np 2 import matplotlib.pyplot as plt 3 from mpl_toolkits.mplot3d import Axes3D 4 from mpl_toolkits.mplot3d.art3d import Poly3DCollection 5 from matplotlib.patches import Rectangle 6 7 dataSize = 500 8 trainDataRatio = 0.3 9 ita = 0.3 10 defaultTrainRatio = 0.3 # 故意减少简单分类器的训练轮数 11 randomSeed = 103 12 13 def myColor(x): # 颜色函数 14 r = np.select([x < 1/2, x < 3/4, x <= 1, True],[0, 4 * x - 2, 1, 0]) 15 g = np.select([x < 1/4, x < 3/4, x <= 1, True],[4 * x, 1, 4 - 4 * x, 0]) 16 b = np.select([x < 1/4, x < 1/2, x <= 1, True],[1, 2 - 4 * x, 0, 0]) 17 return [r**2,g**2,b**2] 18 19 def dataSplit(dataX, dataY, part): # 将数据集分割为训练集和测试集 20 return dataX[:part,:],dataY[:part], dataX[part:,:], dataY[part:] 21 22 def function(x,para): # 连续回归函数,用于画图 23 return np.sum(x * para[0]) - para[1] # 注意是减号 24 25 def judgeWeak(x, para): # 弱分类判别函数 26 return np.sign(function(x, para)) 27 28 def judgeStrong(x, paraList , alpha): # 强分类判别函数,调用弱分类判别函数进行线性加和 29 return np.sign( np.sum([ judgeWeak(x, paraList[i]) * alpha[i] for i in range(len(paraList)) ]) ) 30 31 def targetIndex(x, xList): # 二分查找 xList 中不大于 x 的最大索引 32 lp = 0 33 rp = len(xList) - 1 34 mp = mp = (lp + rp) >> 1 35 while lp < mp: 36 if(xList[mp] > x): 37 rp = mp 38 else: 39 lp = mp 40 mp = (lp + rp) >> 1 41 return mp 42 43 def createData(dim, count = dataSize): # 创建数据 44 np.random.seed(randomSeed) 45 X = np.random.rand(count, dim) 46 if dim == 1: 47 Y = (X > 0.5).astype(int).flatten() * 2 - 1 48 else: 49 Y = ((3 - 2 * dim) * X[:,0] + 2 * np.sum(X[:,1:], 1) > 0.5).astype(int) * 2 - 1 50 print( "dim = %d, dataSize = %d, class1Ratio = %f"%(dim, count, np.sum((Y == 1).astype(int)) / count) ) 51 return X, Y 52 53 def perceptron(dataX, dataY, weight, trainRatio = defaultTrainRatio): # 单层感知机,只训练 dataX 中占比为 trainRatio 的数据 54 count, dim = np.shape(dataX) 55 xE = np.concatenate((dataX, -np.ones(count)[:,np.newaxis]), axis = 1) 56 w = np.zeros(dim + 1) 57 accWeight = np.cumsum(weight) # 累加分布列用于随机选取 58 finishFlag = False 59 for i in range(int(count * trainRatio)): 60 j = targetIndex(np.random.rand(), accWeight) # 依分布列随机抽取一个样本进行训练 61 w += ita * (dataY[j] - np.sign(np.sum(xE[j] * w))) * xE[j] 62 return (w[:-1],w[-1]) 63 64 def adaBoost(dataX, dataY, weakCount): # 提升训练 65 count, dim = np.shape(dataX) 66 weight = np.ones(count) / count # 样本权重 67 paraList = [] # 弱分类器的系数 68 alpha = np.zeros(weakCount) # 弱分类器的权重 69 for i in range(weakCount): 70 para = perceptron(dataX, dataY, weight) # 每次训练后检查训练集的分类情况,调整弱分类器权重和样本权重 71 trainResult = [ judgeWeak(i, para) for i in dataX ] 72 trainErrorRatio = np.sum( (np.array(trainResult) != dataY).astype(int) * weight ) 73 paraList.append(para) 74 alpha[i] = np.log(1 / (trainErrorRatio + 1e-8) - 1) / 2 75 weight *= np.exp( -alpha[i] * dataY * trainResult ) 76 weight /= np.sum(weight) 77 return paraList, alpha 78 79 def test(dim, weakCount): # 测试函数 80 allX, allY = createData(dim) 81 trainX, trainY, testX,testY = dataSplit(allX, allY, int(dataSize * trainDataRatio)) 82 83 paraList, alpha = adaBoost(trainX, trainY, weakCount) 84 85 testResult = [ judgeStrong(i, paraList, alpha) for i in testX ] 86 errorRatio = np.sum( (np.array(testResult) != testY).astype(int)**2 ) / (dataSize*(1-trainDataRatio)) 87 print( "dim = %d, weakCount = %d, errorRatio = %f"%(dim, weakCount, round(errorRatio,4)) ) 88 for i in range(weakCount): 89 print(alpha[i] , "\t\t", paraList[i]) 90 91 if dim >= 4: # 4维以上不画图,只输出测试错误率 92 return 93 94 classP = [ [],[] ] 95 errorP = [] 96 for i in range(len(testX)): 97 if testResult[i] != testY[i]: 98 if dim == 1: 99 errorP.append(np.array([testX[i], int(testY[i]+1)>>1])) 100 else: 101 errorP.append(np.array(testX[i])) 102 else: 103 classP[int(testResult[i]+1)>>1].append(testX[i]) 104 errorP = np.array(errorP) 105 classP = [ np.array(classP[0]), np.array(classP[1]) ] 106 107 fig = plt.figure(figsize=(10, 8)) 108 if dim == 1: 109 plt.xlim(0.0,1.0) 110 plt.ylim(-0.25,1.25) 111 for i in range(2): 112 if(len(classP[i])) > 0: 113 plt.scatter(classP[i], np.ones(len(classP[i])) * i, color = myColor(i/2), s = 8, label = "class" + str(i)) 114 if len(errorP) != 0: 115 plt.scatter(errorP[:,0], errorP[:,1],color = myColor(1), s = 16,label = "errorData") 116 117 plt.plot([0.5, 0.5], [-0.25, 1.25], color = [0.5,0.25,0],label = "realBoundary") 118 plt.text(0.2, 1.1, "realBoundary: 2x = 1\nerrorRatio = " + str(round(errorRatio,4)),119 size=15, ha="center", va="center", bbox=dict(boxstyle="round", ec=(1., 0.5, 0.5), fc=(1., 1., 1.))) 120 R = [ Rectangle((0,0),0,0, color = myColor(i / 2)) for i in range(2) ] + [ Rectangle((0,0),0,0, color = myColor(1)), Rectangle((0,0),0,0, color = [0.5,0.25,0]) ] 121 plt.legend(R, [ "class" + str(i) for i in range(2) ] + ["errorData", "realBoundary"], loc=[0.81, 0.2], ncol=1, numpoints=1, framealpha = 1) 122 123 if dim == 2: 124 plt.xlim(-0.1, 1.1) 125 plt.ylim(-0.1, 1.1) 126 for i in range(2): 127 if(len(classP[i])) > 0: 128 plt.scatter(classP[i][:,0], classP[i][:,1], color = myColor(i/2), s = 8, label = "class" + str(i)) 129 if len(errorP) != 0: 130 plt.scatter(errorP[:,0], errorP[:,1], color = myColor(1), s = 16, label = "errorData") 131 plt.plot([0,1], [1/4,3/4], color = [0.5,0.25,0], label = "realBoundary") 132 plt.text(0.78, 1.02, "realBoundary: -x + 2y = 1\nerrorRatio = " + str(round(errorRatio,4)), 133 size = 15, ha="center", va="center", bbox=dict(boxstyle="round", ec=(1., 0.5, 0.5), fc=(1., 1., 1.))) 134 R = [ Rectangle((0,0),0,0, color = myColor(i / 2)) for i in range(2) ] + [ Rectangle((0,0),0,0, color = myColor(1)) ] 135 plt.legend(R, [ "class" + str(i) for i in range(2) ] + ["errorData"], loc=[0.84, 0.012], ncol=1, numpoints=1, framealpha = 1) 136 137 if dim == 3: 138 ax = Axes3D(fig) 139 ax.set_xlim3d(0.0, 1.0) 140 ax.set_ylim3d(0.0, 1.0) 141 ax.set_zlim3d(0.0, 1.0) 142 ax.set_xlabel(‘X‘, fontdict={‘size‘: 15, ‘color‘: ‘k‘}) 143 ax.set_ylabel(‘Y‘, fontdict={‘size‘: 15, ‘color‘: ‘k‘}) 144 ax.set_zlabel(‘Z‘, fontdict={‘size‘: 15, ‘color‘: ‘k‘}) 145 for i in range(2): 146 if(len(classP[i])) > 0: 147 ax.scatter(classP[i][:,0], classP[i][:,1], classP[i][:,2], color = myColor(i/2), s = 8, label = "class" + str(i)) 148 if len(errorP) != 0: 149 ax.scatter(errorP[:,0], errorP[:,1],errorP[:,2], color = myColor(1), s = 8, label = "errorData") 150 v = [(0, 0, 0.25), (0, 0.25, 0), (0.5, 1, 0), (1, 1, 0.75), (1, 0.75, 1), (0.5, 0, 1)] 151 f = [[0,1,2,3,4,5]] 152 poly3d = [[v[i] for i in j] for j in f] 153 ax.add_collection3d(Poly3DCollection(poly3d, edgecolor = ‘k‘, facecolors = [0.5,0.25,0,0.5], linewidths=1)) 154 ax.text3D(0.75, 0.92, 1.15, "realBoundary: -3x + 2y +2z = 1\nerrorRatio = " + str(round(errorRatio,4)), 155 size = 12, ha="center", va="center", bbox=dict(boxstyle="round", ec=(1, 0.5, 0.5), fc=(1, 1, 1))) 156 R = [ Rectangle((0,0),0,0, color = myColor(i / 2)) for i in range(2) ] + [ Rectangle((0,0),0,0, color = myColor(1)) ] 157 plt.legend(R, [ "class" + str(i) for i in range(2) ] + ["errorData"], loc=[0.84, 0.012], ncol=1, numpoints=1, framealpha = 1) 158 159 fig.savefig("R:\\dim" + str(dim) + "kind2" + "weakCount" + str(weakCount) + ".png") 160 plt.close() 161 162 if __name__ == ‘__main__‘: 163 test(1, 1) # 不同维数和弱分类器数的组合 164 test(1, 2) 165 test(1, 3) 166 test(1, 4) 167 test(2, 1) 168 test(2, 2) 169 test(2, 3) 170 test(2, 4) 171 test(3, 1) 172 test(3, 2) 173 test(3, 3) 174 test(3, 4) 175 test(4, 1) 176 test(4, 2) 177 test(4, 3) 178 test(4, 4)
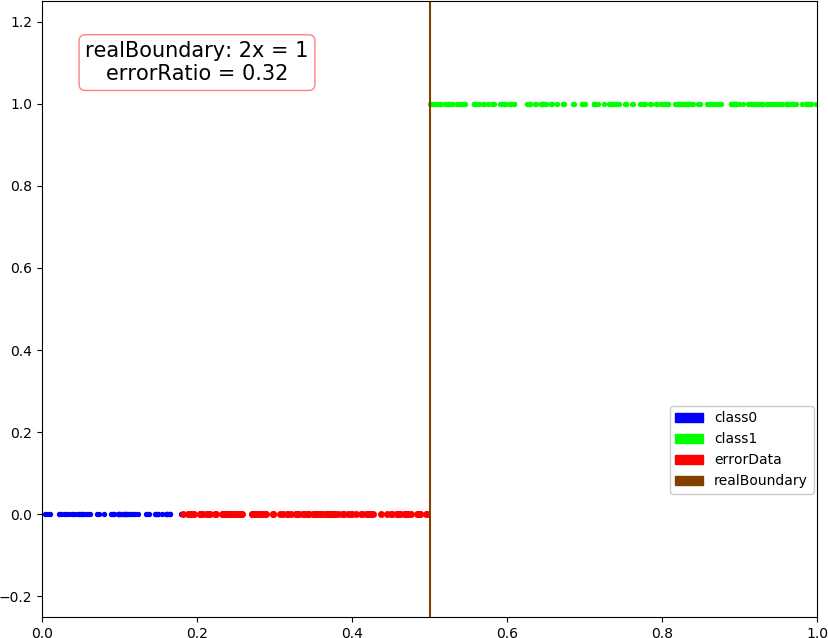
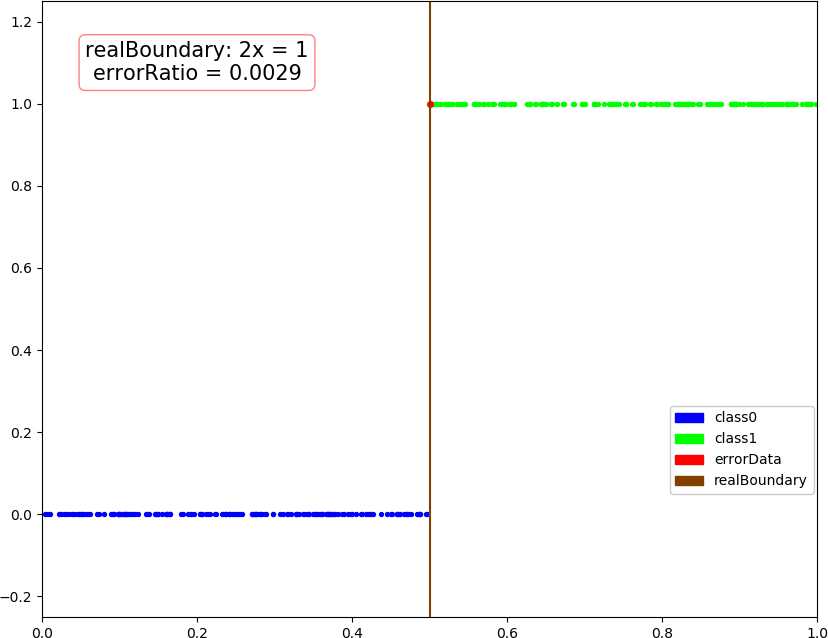
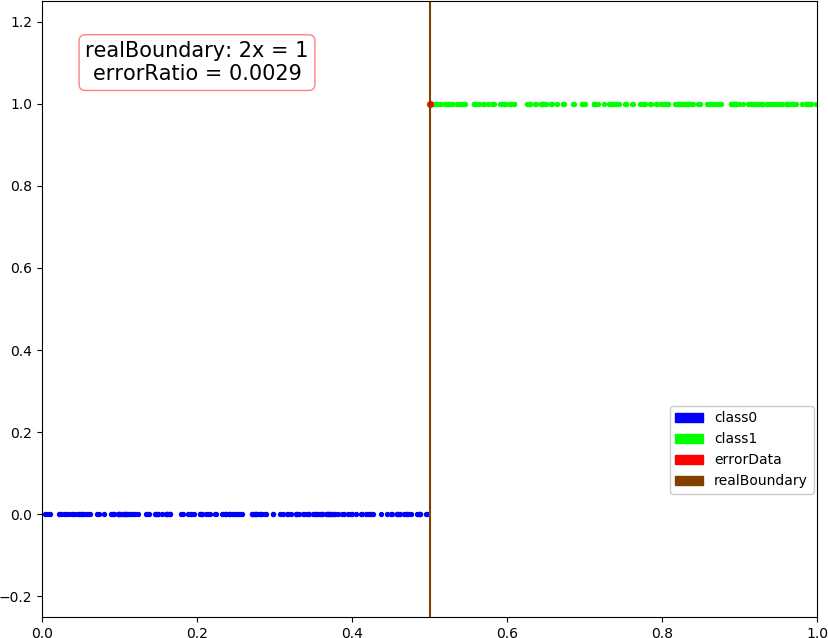
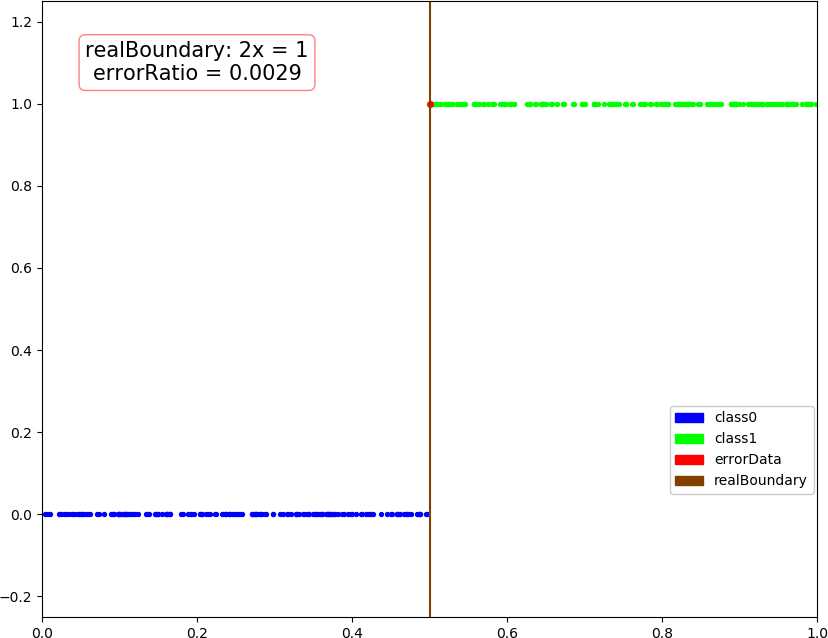
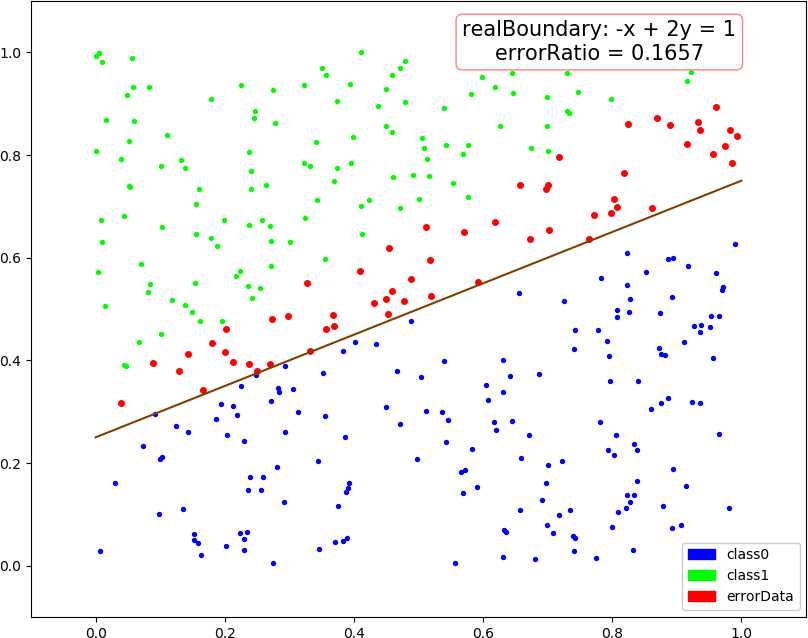
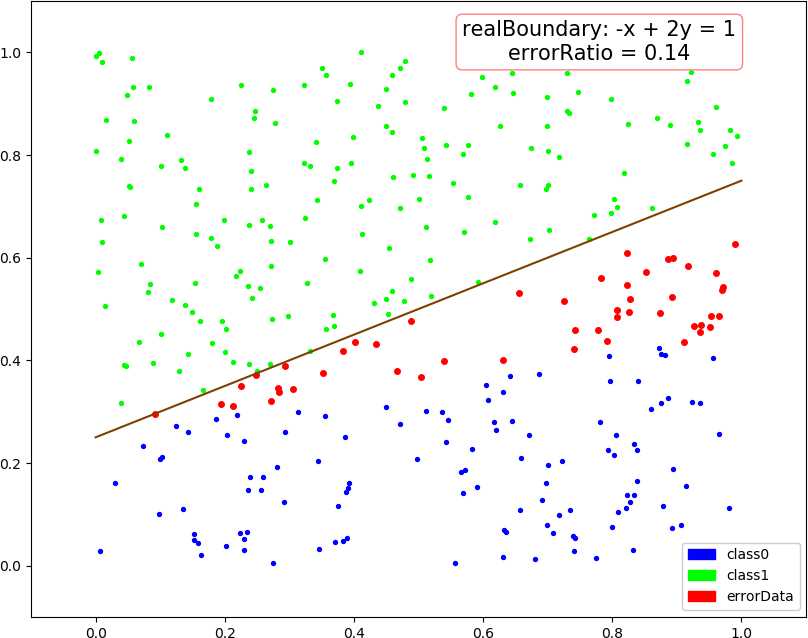
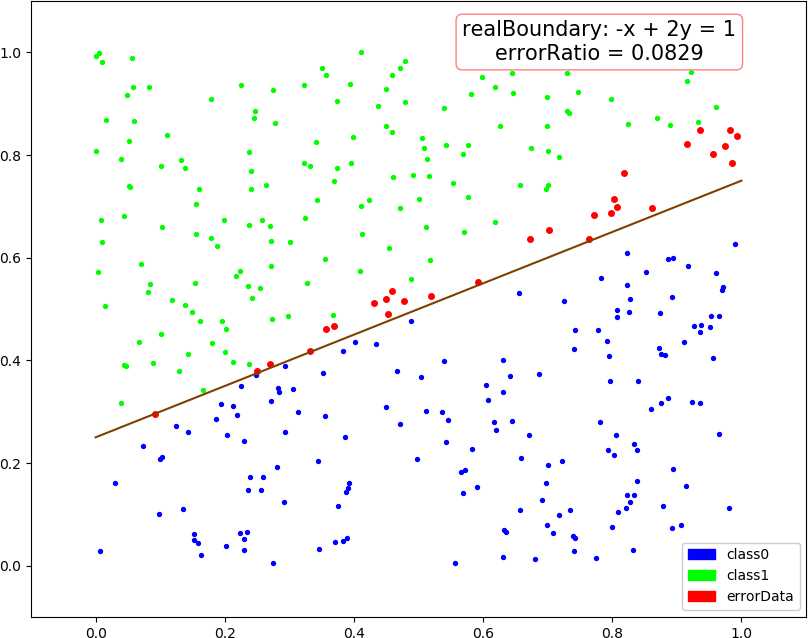
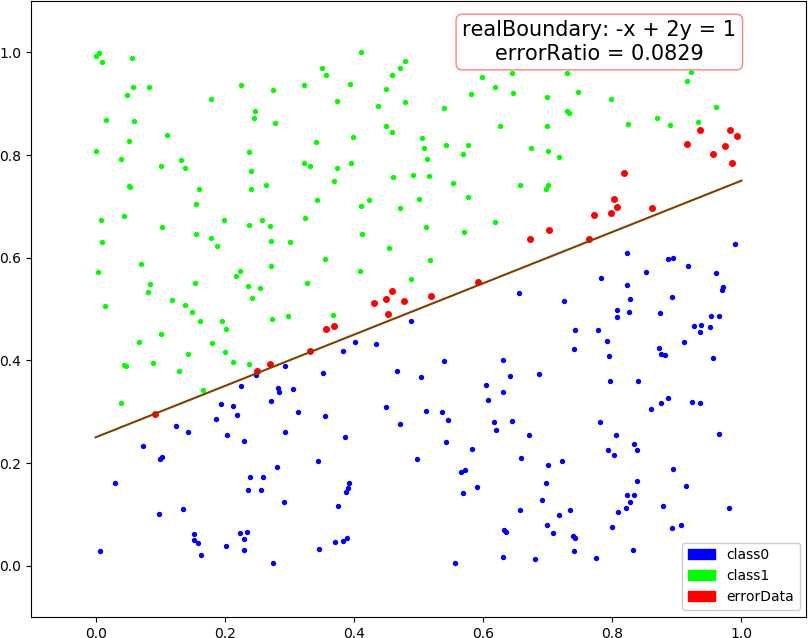
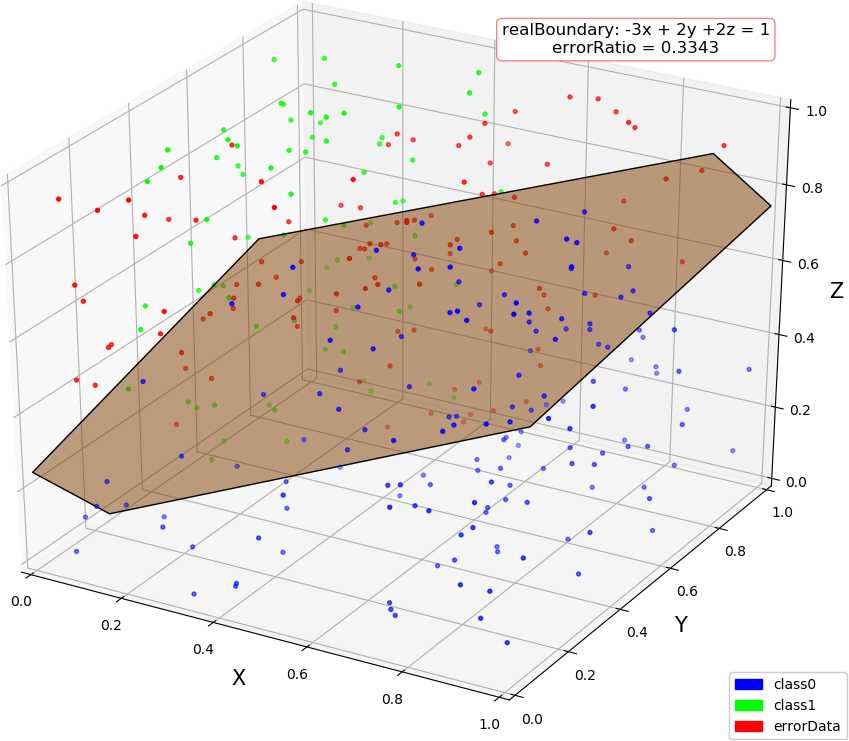
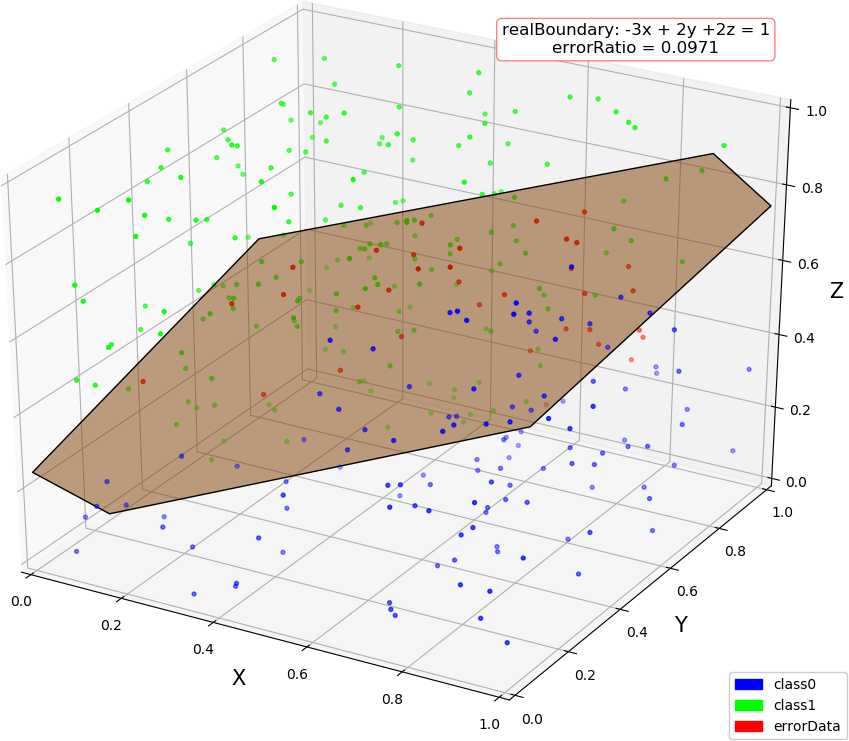
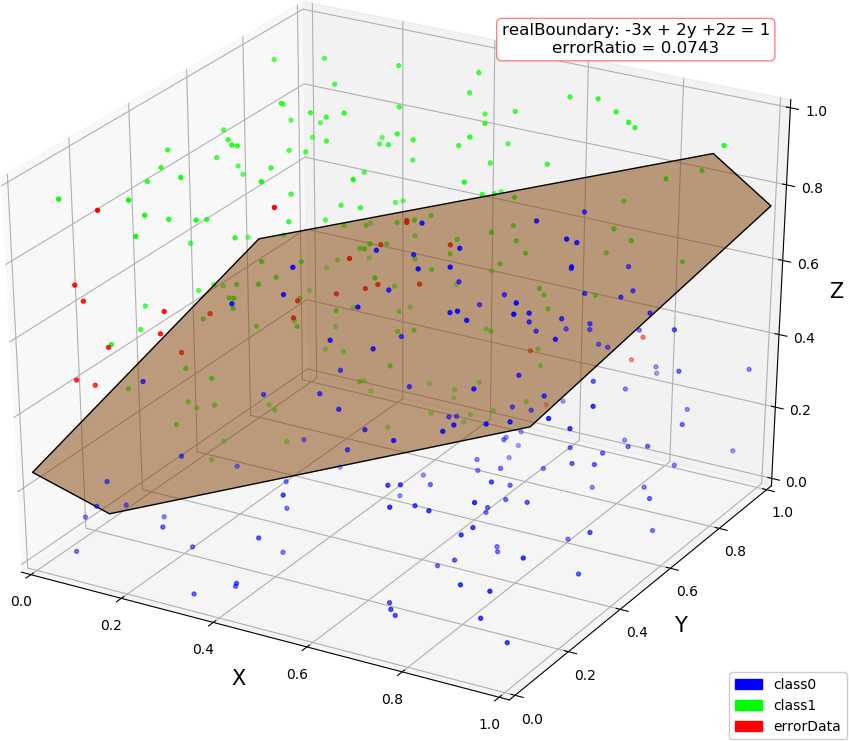
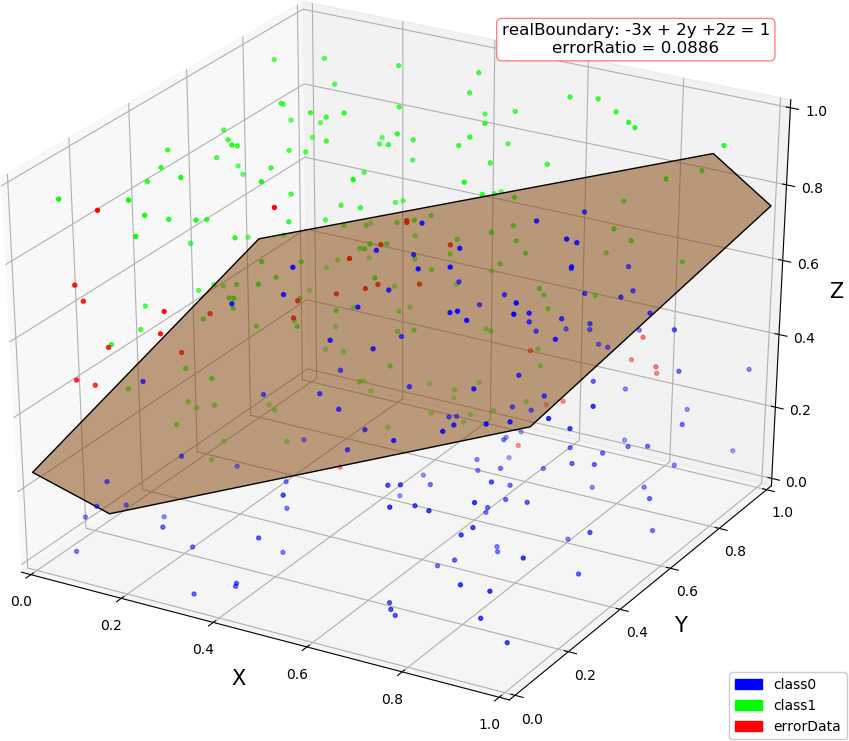
● 输出结果,随着使用的弱分类器数量的增多,预测精度逐渐上升。低维情况不明显,少数的弱分类器就已经达到了较好的精度,高维情况中,精度上升会抖动,被分类的点在分类结果中也会抖动。
dim = 1, dataSize = 500, class1Ratio = 0.492000 dim = 1, weakCount = 1, errorRatio = 0.320000 0.34657356777997284 (array([1.67141915]), 0.29999999999999993) dim = 1, dataSize = 500, class1Ratio = 0.492000 dim = 1, weakCount = 2, errorRatio = 0.002900 0.34657356777997284 (array([1.67141915]), 0.29999999999999993) 2.6466513960316105 (array([0.59811356]), 0.3) dim = 1, dataSize = 500, class1Ratio = 0.492000 dim = 1, weakCount = 3, errorRatio = 0.002900 0.34657356777997284 (array([1.67141915]), 0.29999999999999993) 2.6466513960316105 (array([0.59811356]), 0.3) 1.154062035731127 (array([0.70689064]), 0.29999999999999993) dim = 1, dataSize = 500, class1Ratio = 0.492000 dim = 1, weakCount = 4, errorRatio = 0.002900 0.34657356777997284 (array([1.67141915]), 0.29999999999999993) 2.6466513960316105 (array([0.59811356]), 0.3) 1.154062035731127 (array([0.70689064]), 0.29999999999999993) 0.41049029622924904 (array([0.65816408]), 0.29999999999999993) dim = 2, dataSize = 500, class1Ratio = 0.520000 dim = 2, weakCount = 1, errorRatio = 0.165700 0.7581737108087062 (array([-0.5342485 , 0.85301855]), 0.3) dim = 2, dataSize = 500, class1Ratio = 0.520000 dim = 2, weakCount = 2, errorRatio = 0.140000 0.7581737108087062 (array([-0.5342485 , 0.85301855]), 0.3) 1.1603017192470149 (array([-0.23046473, 1.17772171]), 0.29999999999999993) dim = 2, dataSize = 500, class1Ratio = 0.520000 dim = 2, weakCount = 3, errorRatio = 0.082900 0.7581737108087062 (array([-0.5342485 , 0.85301855]), 0.3) 1.1603017192470149 (array([-0.23046473, 1.17772171]), 0.29999999999999993) 1.366866794214113 (array([-0.86403595, 1.29893022]), 0.3) dim = 2, dataSize = 500, class1Ratio = 0.520000 dim = 2, weakCount = 4, errorRatio = 0.082900 0.7581737108087062 (array([-0.5342485 , 0.85301855]), 0.3) 1.1603017192470149 (array([-0.23046473, 1.17772171]), 0.29999999999999993) 1.366866794214113 (array([-0.86403595, 1.29893022]), 0.3) -0.07595124913479236 (array([-0.71435958, 1.09996259]), 0.3) dim = 3, dataSize = 500, class1Ratio = 0.544000 dim = 3, weakCount = 1, errorRatio = 0.334300 0.4236489063840784 (array([-1.88583778, 1.00159772, 0.23076269]), 0.3) dim = 3, dataSize = 500, class1Ratio = 0.544000 dim = 3, weakCount = 2, errorRatio = 0.097100 0.4236489063840784 (array([-1.88583778, 1.00159772, 0.23076269]), 0.3) 1.2147383422658522 (array([-1.11207425, 0.87462922, 1.16116403]), 0.29999999999999993) dim = 3, dataSize = 500, class1Ratio = 0.544000 dim = 3, weakCount = 3, errorRatio = 0.074300 0.4236489063840784 (array([-1.88583778, 1.00159772, 0.23076269]), 0.3) 1.2147383422658522 (array([-1.11207425, 0.87462922, 1.16116403]), 0.29999999999999993) 1.4030555888409086 (array([-0.90813279, 0.97916935, 0.44726373]), 0.3) dim = 3, dataSize = 500, class1Ratio = 0.544000 dim = 3, weakCount = 4, errorRatio = 0.088600 0.4236489063840784 (array([-1.88583778, 1.00159772, 0.23076269]), 0.3) 1.2147383422658522 (array([-1.11207425, 0.87462922, 1.16116403]), 0.29999999999999993) 1.4030555888409086 (array([-0.90813279, 0.97916935, 0.44726373]), 0.3) 0.298249916659031 (array([-0.92372522, 1.11109598, 0.9864088 ]), -0.30000000000000004) dim = 4, weakCount = 1, errorRatio = 0.271400 0.6328331575281093 (array([-1.55413592, 1.59665079, 0.46795061, 1.01271949]), 0.29999999999999993) dim = 4, dataSize = 500, class1Ratio = 0.484000 dim = 4, weakCount = 2, errorRatio = 0.271400 0.6328331575281093 (array([-1.55413592, 1.59665079, 0.46795061, 1.01271949]), 0.29999999999999993) 0.4566505516305031 (array([-2.06478282, -0.07030723, 0.28072944, 0.50215833]), 0.30000000000000004) dim = 4, dataSize = 500, class1Ratio = 0.484000 dim = 4, weakCount = 3, errorRatio = 0.271400 0.6328331575281093 (array([-1.55413592, 1.59665079, 0.46795061, 1.01271949]), 0.29999999999999993) 0.4566505516305031 (array([-2.06478282, -0.07030723, 0.28072944, 0.50215833]), 0.30000000000000004) 0.1788001854725199 (array([-1.57793113, 1.11981 , 0.68428309, 0.48606427]), -0.3) dim = 4, dataSize = 500, class1Ratio = 0.484000 dim = 4, weakCount = 4, errorRatio = 0.177100 0.6328331575281093 (array([-1.55413592, 1.59665079, 0.46795061, 1.01271949]), 0.29999999999999993) 0.4566505516305031 (array([-2.06478282, -0.07030723, 0.28072944, 0.50215833]), 0.30000000000000004) 0.1788001854725199 (array([-1.57793113, 1.11981 , 0.68428309, 0.48606427]), -0.3) 0.8838043587493469 (array([-1.46314889, 0.7044062 , 0.47142833, 0.2926442 ]), 0.3)
● 画图,行:数据维数,列:分别使用 1 ~ 4 个弱分类器
标签:alpha size mat new 抖动 nat round too real
原文地址:https://www.cnblogs.com/cuancuancuanhao/p/11285960.html