标签:需要 img 计算机 bsp src 地方 不同的 情况 png
将没有标签的样本分成不同的集合(簇),这种算法叫做聚类。常用的领域有市场分割、社交网络分析、计算机集群管理、了解星系等。
(1)K-均值是最普及的聚类算法,是一种迭代算法,假设需要将数据聚类成n个组,这时候首先随机选择K个点,称为聚类中心。
将每个样本归属到最近的聚类中心,然后重新计算每个类的中心变成新的聚类中心,重复以上步骤,直到聚类中心不变。
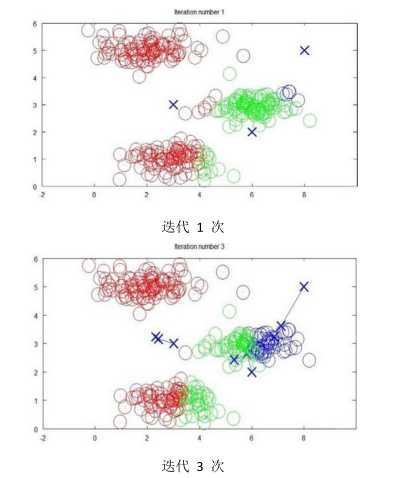
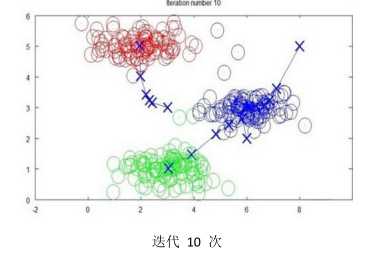
伪代码如下:

k-均值的最小化问题,就是每个样本点到对应聚类中心的距离之和:
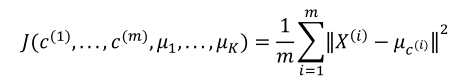
与其他算法不同的是,k-均值每一次迭代都会是代价函数变小。
(1)K应该小于样本数m;
(2)从样本中随机选取K个实例作为初始聚类中心。
K-均值可能会出现局部最小的情况,如下所示:
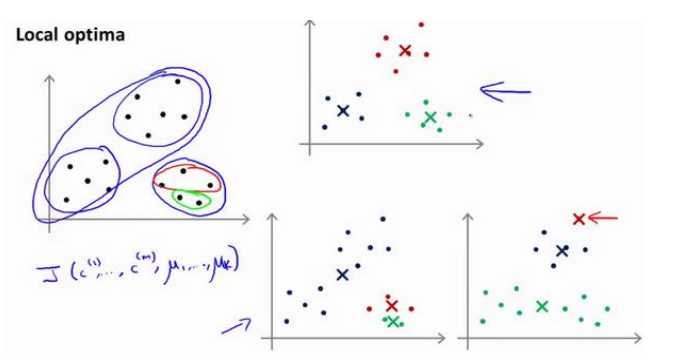
解决方案:多次运行该算法,最后在比较K-均值代价函数最小的结果,这种方法适用于K取较小的时候(2-10),K太大没有明显效果。
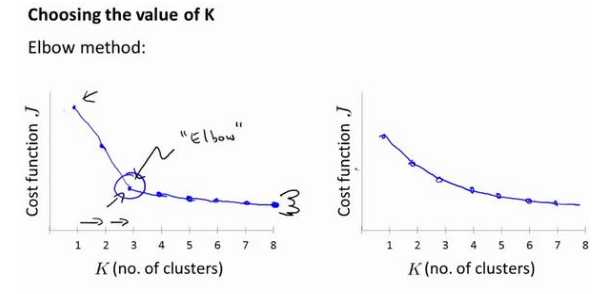
绘制聚类数与代价函数的图,然后选取出现斜率突然变小的地方的值(“肘部法则”)。

标签:需要 img 计算机 bsp src 地方 不同的 情况 png
原文地址:https://www.cnblogs.com/henuliulei/p/11286955.html