数论夏夜实战，然夯实基础尤为重要！

标签：简单   重要   并且   multiple   mon   problem   简单的   src   因子   

____________________________我往前飞   飞过一片时间海

1.

关于同余式的约去法则：

给出一个正整数m和三个整数a, b和c，d=GCD(c, m)，并且ac≡bc(mod m)。则a≡b(mod (m DIV d))。

2.___________________________________大数用于是被其因子这些小数整除的！

我们已经定义了两个数 a 和 b 的最大公约数 (a,b) .关于这个数有一个简单的公式　　　　|  （a，b) = GCD(a,b)!

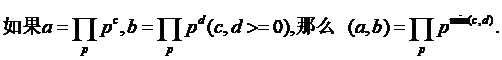
这是 min(c,d) 鸭子！

两个整数 a和b 的最小公倍数(least common multiple  ) 是同时能被 a和 b整除的最小整数.用{a,b}表示。

于是有： a|{a,b}   ,  b|{a,b}

在上述的记号的情况下，有：

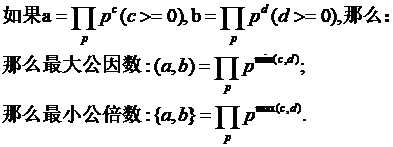图有些糊了，嘻嘻：

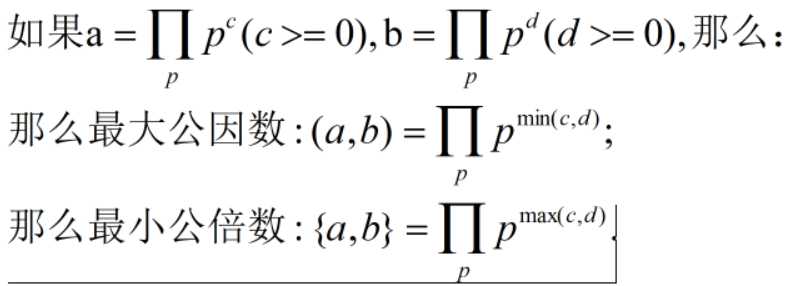
究极总结：

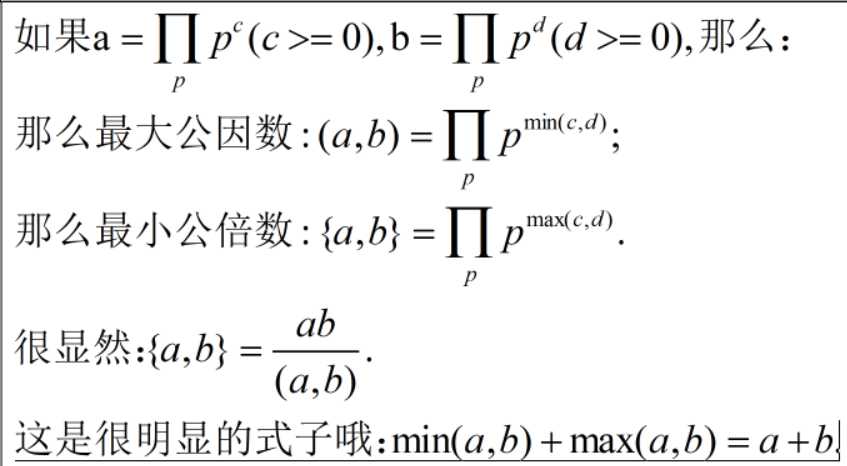
 3.

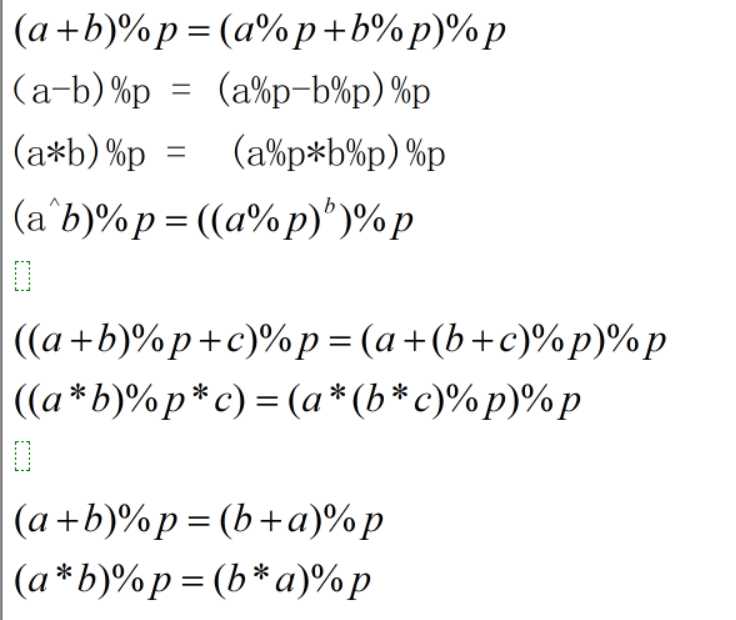
4.有所待：https://vjudge.net/contest/316798#problem/C

观览书籍：

《哈代数论》

数论夏夜实战，然夯实基础尤为重要！

标签：简单   重要   并且   multiple   mon   problem   简单的   src   因子   

原文地址：https://www.cnblogs.com/dragondragon/p/11296845.html