标签:uil 个数 就是 难度 get else include img cst
序列单点修改,区间询问最大连续子段和。
最大子段和难以更新,不过这里的单点修改降低了难度,不用维护标记了。现在要做的就是通过维护数个数据支持最大子段和的查询。
考虑最大子段和是连续子段,如果在这个子段中砍一刀,它仍然是两段:
左边的子段中,紧靠右边的最大子段和
右边的子段中,紧靠左边的最大子段和而反过来,知道了右子段中紧靠左边的最大子段和,左子段中紧靠右边的最大子段和时,就可以还原出这个最大子段。当然,这是在已知中间点(砍的一刀)的情况下。
因为最大子段还有可能在左子段中,与右子段没有公共部分。所以这时的答案就是左子段中的最大子段和。反之则同理。
如图: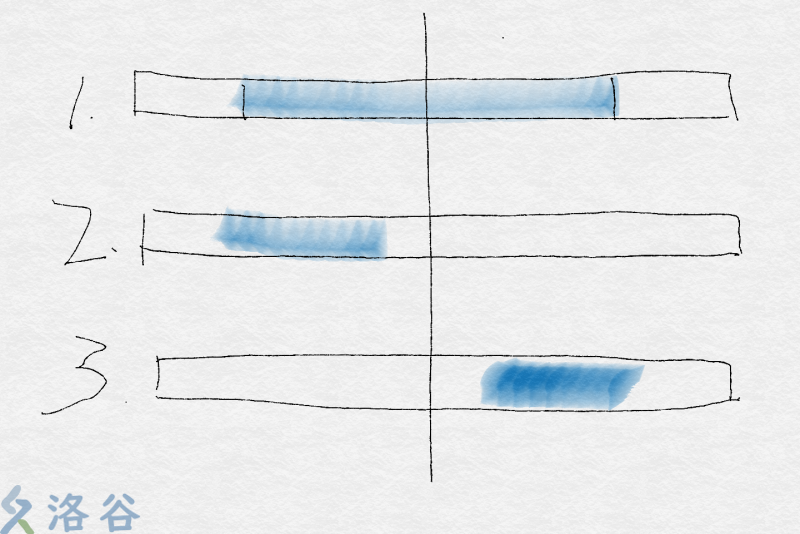
这三个信息就可以拼凑出整个区间的最大子段和了。
所以维护四个信息:区间和,最大子段和,紧靠左边的最大子段和,紧靠右边的最大子段和。
紧靠左边的最大子段和,紧靠右边的最大子段需要利用区间和才可以\(O(1)\)更新。这部分很好模拟,不懂的可以看代码。
#include<iostream>
#include<cstdio>
using namespace std;
const int MAXN=50005;
int n,m,a[MAXN],sum[MAXN<<2],maxs[MAXN<<2],lefts[MAXN<<2],rights[MAXN<<2];
int u,v,w;
struct data{
int _sum,_maxs,_lefts,_rights;
};
inline void upd(int x)
{
sum[x]=sum[x<<1]+sum[x<<1|1];
maxs[x]=max(max(maxs[x<<1],maxs[x<<1|1]),rights[x<<1]+lefts[x<<1|1]);
lefts[x]=max(sum[x<<1]+lefts[x<<1|1],lefts[x<<1]);
rights[x]=max(rights[x<<1]+sum[x<<1|1],rights[x<<1|1]);
}
inline void build(int x,int l,int r)
{
int mid=(l+r)>>1;
if(l==r)
{
sum[x]=a[l];
maxs[x]=a[l];
lefts[x]=a[l];
rights[x]=a[l];
return;
}
build(x<<1,l,mid);
build(x<<1|1,mid+1,r);
upd(x);
}
inline data query(int x,int l,int r,int ql,int qr)
{
int mid=(l+r)>>1;
data temp,lt,rt;
if(ql<=l&&r<=qr)
{
temp._sum=sum[x];
temp._maxs=maxs[x];
temp._lefts=lefts[x];
temp._rights=rights[x];
return temp;
}
if(ql<=mid) lt=query(x<<1,l,mid,ql,qr);
if(mid<qr) rt=query(x<<1|1,mid+1,r,ql,qr);
if(ql<=mid&&mid<qr)
{
temp._sum=lt._sum+rt._sum;
temp._maxs=max(lt._rights+rt._lefts,max(lt._maxs,rt._maxs));
temp._lefts=max(lt._lefts,lt._sum+rt._lefts);
temp._rights=max(rt._rights,lt._rights+rt._sum);
return temp;
} else {
if(ql<=mid) return lt;
else return rt;
}
}
inline void modify(int x,int l,int r,int target,int num)
{
if(l==r&&r==target)
{
sum[x]=num;
maxs[x]=num;
lefts[x]=num;
rights[x]=num;
} else {
int mid=(l+r)>>1;
if(target<=mid) modify(x<<1,l,mid,target,num);
if(mid<target) modify(x<<1|1,mid+1,r,target,num);
upd(x);
}
}
signed main()
{
ios::sync_with_stdio(false);
cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i];
build(1,1,n);
cin>>m;
for(register int i=1;i<=m;i++)
{
cin>>u>>v>>w;
if(u==0) modify(1,1,n,v,w);
if(u==1) cout<<query(1,1,n,v,w)._maxs<<"\n";
}
return 0;
}SP1716 GSS3 - Can you answer these queries III
标签:uil 个数 就是 难度 get else include img cst
原文地址:https://www.cnblogs.com/ehznehc/p/11296935.html