标签:ide 读取 bsp har span 补充 case position sum
数据集包含某年9月份欧洲用户在两天时间里发生的284807宗交易,其中包括492宗诈骗。项目通过描述性分析探索诈骗案的相关特点和模式,再通过机器学习算法创建预测模型、调参,并通过混淆矩阵等方法选择模型。
library(data.table) # fread() # 载入数据 cards<-fread("D:/R/practise/……/creditcard.csv") # 原始数据集有143MB,用数据操作包data.table,fread函数读取速度是原生函数的近10倍。
查看数据总体情况、变量类型、缺失值、 异常值、分布类型等等
library(VIM) # aggr()
# 查看数据总体情况,建立数据词典
str(cards) summary(cards) aggr(cards) # 可视化缺失值 # 其他判断缺失值办法:table(is.na(cards)) # 查看样本数据分布 prop.table(table(cards$Class)) # 正例为仅为0.001727486 qplot(x=cards$Class,data=cards,geom="bar",fill=cards$Class) # 可视化效果
数据词典
缺失值情况:无
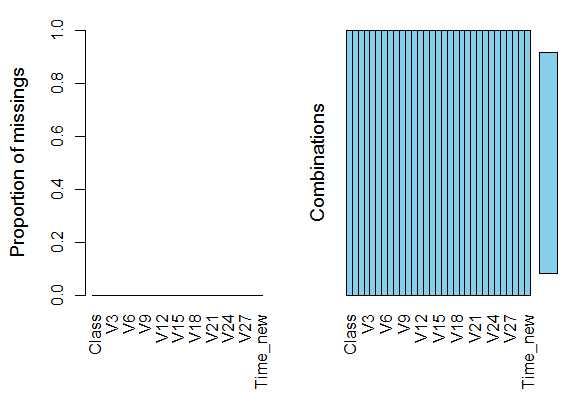
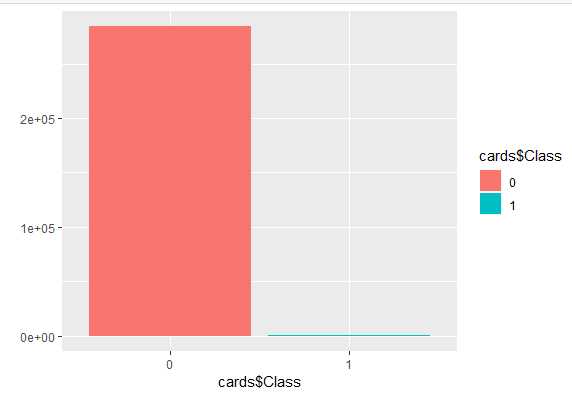
样本分布情况:正类仅为0.001727486,占比例非常低,据此训练的模型,对正类(诈骗)案件不敏感,会更偏向识别正常交易。在训练模型时候需要对训练集做调整(详情见后)
# 数据塑形 时间转换 秒——小时 cards$Time_new<-round(cards$Time/3600,0) # 将时间以秒为单位转换为 以小时为单位 cards$Time<-NULL # 数据集中原时间变量已经无效,可删 cards<-cards %>% select(Class,everything()) # 将变量Class调整到第一列 class(cards$Class) cards$Class<-as.factor(cards$Class) # 变量class转换为因子型
# 解决数据失衡问题
cards_0<-cards[cards$Class==‘0‘] # 正常 非诈骗交易
cards_1<-cards[cards$Class==‘1‘] # 诈骗案例
index1<-sample(1:nrow(cards_0),size = nrow(cards_1))
# 合并数据集
cards_new<-rbind(cards_1,cards_0[index1])
# 归一化处理
library(caret)
standard <- preProcess(cards_new, method = ‘range‘) # caret包中函数,range表示区间为[-1:1]
card_new2 <- predict(standard, cards_new)
traindata_2 <- card_new2[index2, ] # index2 见52行
testdata_2 <- card_new2[-index2, ]
# 对新数据集进行做训练集、测试集的划分 index2<-createDataPartition(cards_new$Class,times = 1,p=.7,list = F) train_cards<-cards_new[index2,] # 训练集 test_cards<-cards_new[-index2,] # 测试集
数据集中第2列到第28列都是PCA数据,无法做有效描述性统计分析,故这里主要基于时间、金额等进行分析。
# 诈骗案发生时间、金额分布 p1<-ggplot(cards_1,aes(x=factor(Time_new),fill=factor(Time_new)))+ geom_bar(stat = ‘count‘)+ labs(title = ‘Time Distribution of\nFraud Cases‘,x=‘Time‘,y=‘Count‘)+ theme_classic()+ theme(legend.position=‘none‘) # 计算每小时诈骗案涉及金额 # cards_1$Time_new<-as.factor(as.character(cards_1$Time_new)) Amount_money<-rowsum(cards_1$Amount,group=cards_1$Time_new) # 数据准备 Amount_c<-Amount_money[,1] Time_c<-0:47 DF_money<-data.frame(Time_c,Amount_c) p2<-ggplot(DF_money,aes(x=factor(Time_c),y=Amount_c,fill=Time_c))+ geom_bar(stat = ‘identity‘)+ labs(title = ‘Distribution bar chart of \nfraud amount‘,x=‘Time‘)+ theme(legend.position=‘none‘) library(Rmisc) multiplot(p1,p2,cols = 1)
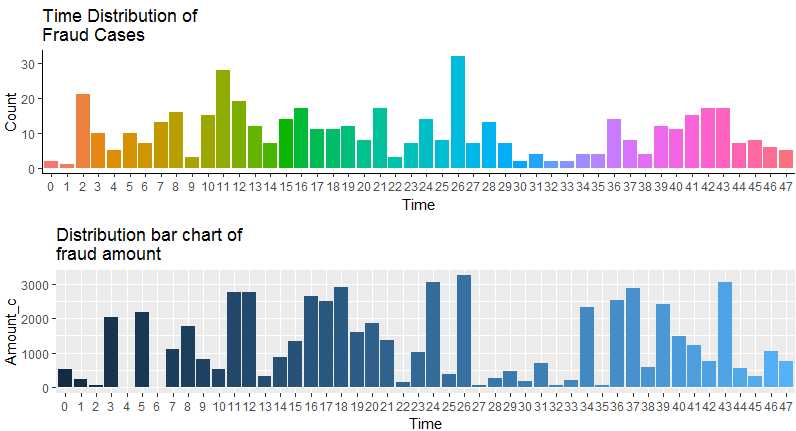
描述性分析结论:
从总趋势说,第一天多余第二天(但因为没有更多的数据,更长的时间轴,这一点无法得出有效结论);
整体看每小时平均诈骗数量在10次以下,涉案金额在500欧元左右;
从时间上说,诈骗发生次数在一天中的后半夜居多;
从涉案金额来说,而平均诈骗金额基本与次数相对应。其中第二天凌晨两点发生次数最多,30余起,对应的金额也是最大,超过3000欧元。
# 使用五折交叉验证方法建立随机森林模型
set.feed(1234) model_rf <- train(Class ~., data = train_cards, method = ‘rf‘, trControl = trainControl(method = ‘cv‘, number = 5, selectionFunction = ‘oneSE‘)) # 利用训练集建立随机森林模型 pred_model<-predict(model_rf,test_cards[,-1]) # 测试模型 confusionMatrix(data=pred_model,reference=test_cards$Class) # 准确率为94.9% plot(varImp(model_rf)) # 查看模型中变量的重要程度
查看模型:
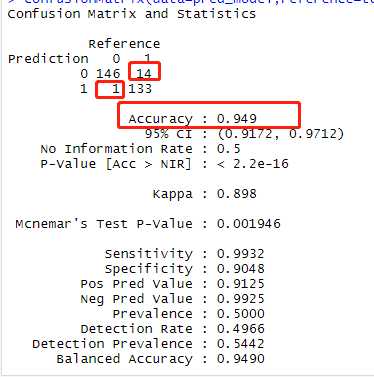
查看模型中变量的重要程度:
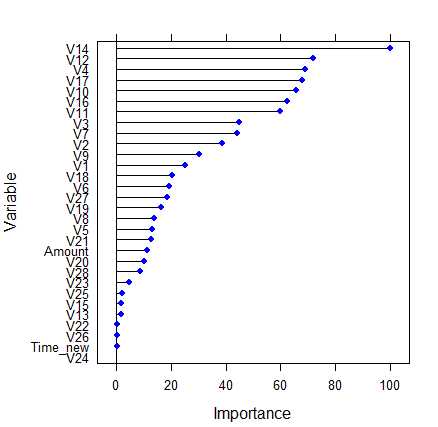
results = c() # 创建一个空向量 for(i in 1:10) { set.seed(1234) pred_knn <- knn(train=traindata_2[,2:30], test=testdata_2[,2:30], cl=traindata_2$Class, i) Table <- table(pred_knn, testdata_2$Class) accuracy <- sum(diag(Table))/sum(Table) # diag()提取对角线上的值 results <- c(results, accuracy) } plot(x = 1:10, y = results, type = ‘b‘, col = ‘blue‘, xlab = ‘k‘, ylab = ‘accuracy‘)
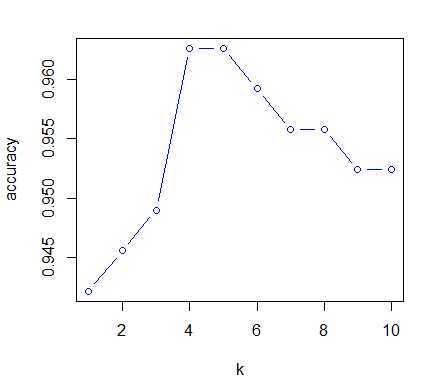
# 根据图像k=4时,准确率最高。 pred_knn <- knn(train=traindata_2[,2:30], test=testdata_2[,2:30], cl=traindata_2$Class, 4) confusionMatrix(pred_knn,testdata_2$Class) # 准确率为95.24%
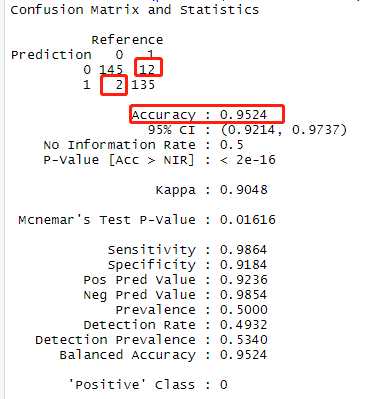
通过随机森林、k近邻算法分别得到model_rf、pred_knn两个模型,下面根据查全率、查准率和kappa三个维度评估模型。

模型pred_knn在查全率、查准率以及kappa三个评估维度上都高于model_rf,其中查准率达到95.24%,在134个诈骗案中,只有1个判断错误,可用性比较高。
为了方便描述,添加包没有放在文前
# 加载添加包 library(data.table) # fread() library(VIM) # aggr() library(caret) # 机器学习相关 library(dplyr) # select() library(ggplot2) # ggplot/qplot library(Rmisc) # multiplot() library(randomForest) # 随机森林 library(class) # knn模型
标签:ide 读取 bsp har span 补充 case position sum
原文地址:https://www.cnblogs.com/Grayling/p/11297576.html