标签:std 完全 mes iso package case apt phi www
自补图的定义: 原图为G , 补图为H (H是在G的完全图上面去掉关于G图的边得到的新图),G和H为同构
同构的定义:
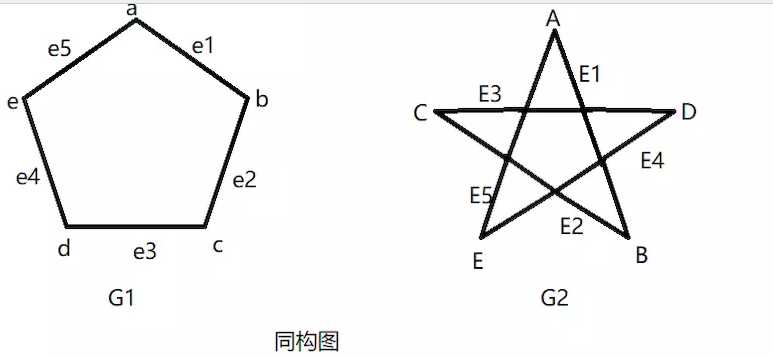
上图中,G1和G2为同构的,因为:
从G1的结点到G2的结点,存在一个一对一的映上函数 f (one - to - one and onto function f )
从G1的边到G2的边,存在一个一对一的映上函数 g (one - to - one and onto function g )
对于某个顺序,如果两个图是同构的,则两个图的邻接矩阵是相同的:
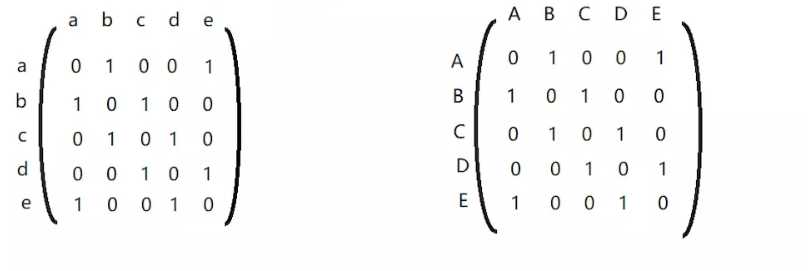
这两个矩阵对应的是上面的两个图
原图与补图边数要一样,所以当n=4*k+2和4*k+3时无解
当n=4*k 时 将点分成4部分P1,P2,P3,P4 前两部分P1P2所有的点两两连边组成团,P3P1部分与部分之间两两连边,P4P2部分与部分之间两两连边
它的补图 是 P3P4组成团,P4P1之间连边,P3P2之间连边,与原图是同构的。
块之间映射关系,原图 P1P2P3P4 补图P3P4P2P1或其他方案。
当n=4*k+1时 剩下一个点随便和两个块连就好了。
图片出场:https://blog.csdn.net/lgz0921/article/details/98455515

#include <bits/stdc++.h>
using namespace std;
int n,a[2500][2500];
void fuck1(int n){
///p1,p2两两全部相连
for (int i = 1; i <= n/2;i++){
for (int j = i+1; j <= n/2;j++){
a[i][j]=1;
a[j][i]=1;
}
}
///p1,p3部分相连 p2,p4部分相连
for (int i = 1; i <= n/4;i++){
for (int j = 1; j <= n/4;j++){
a[i][n/2+j]=1;
a[n/2+j][i]=1;
}
}
for (int i = n/4+1; i <= n/2;i++){
for (int j = n/4+1; j <= n/2;j++){
a[i][n/2+j]=1;
a[n/2+j][i]=1;
}
}
}
void fuck2(int n){
for (int i = 1; i <= n/2;i++){
a[n][i]=1;
a[i][n]=1;
}
n--;
for (int i = 1; i <= n/2;i++){
for (int j = i+1; j <= n/2;j++){
a[i][j]=1;
a[j][i]=1;
}
}
for (int i = 1; i <= n/4;i++){
for (int j = 1; j <= n/4;j++){
a[i][n/2+j]=1;
a[n/2+j][i]=1;
}
}
for (int i = n/4+1; i <= n/2;i++){
for (int j = n/4+1; j <= n/2;j++){
a[i][n/2+j]=1;
a[n/2+j][i]=1;
}
}
}
void print(int n){
for (int i = 1; i <= n;i++){
for (int j = 1; j <= n;j++){
printf("%d",a[i][j]);
}
puts("");
}
if(n==1){
printf("1\n");
return;
}
int x=n;
if(n&1) n--;
for (int i = n; i >= n/2+1;i--){
if(i==n) printf("%d",i);
else printf(" %d",i);
}
for (int i = 1; i <= n/2;i++){
printf(" %d",i);
}
if(x&1) printf(" %d\n",x);
else puts("");
}
int main()
{
int _; scanf("%d",&_);
for(int cas=1 ; cas<=_ ; cas++){
scanf("%d",&n);
printf("Case #%d: ",cas);
if(n%4==2||n%4==3)
{
puts("No");
continue;
}
puts("Yes");
for(int i=1 ; i<=n ; i++)
for(int j=1 ; j<=n ; j++) a[i][j]=0;
if(n%4==0)
{
fuck1(n);
print(n);
}
else
{
fuck2(n);
print(n);
}
}
}
标签:std 完全 mes iso package case apt phi www
原文地址:https://www.cnblogs.com/shuaihui520/p/11306156.html