析合树

时间：2019-08-06 15:27:57 阅读：116 评论：0 收藏：0 [点我收藏+]

标签：++ i+1 连续参考资料映射 VID swa using art

前言

A组的题实在是太与时俱进了……

简介
这是LCAdalao在今年的WC上提出来的算法（也是数据结构），用途是维护一类关于连续段的计数问题。

连续段
先给出几个定义：
序列：\(1\sim n\)的有序集合
段：序列上的一个闭区间\([l,r]\)
置换（排列）：一个双射\(P:A\to A,A_i\to A_{P_i}\)
不动点（连续段）：对于排列\(P\)，定义连续段\((P,[l,r])\)表示一个段，要求\(P_{l\sim r}\)值域是连续的。形式化地说，对于排列\(P\)，连续段是一个段\(Q\)满足\(Q\in I∧P[Q]\in I\)。在以后的叙述中，我们用\(I_P\)表示所有连续段的集合。一个连续段的值域\(ran(S)=[\min_{i\in S}P_i,\max_{i\in S}P_i]\)。

性质
连续段有很多~~可以用显然法证明的~~优美的性质。
两个连续段的交、两个相交连续段的并都是连续段。
如果我们想存储所有的连续段，那么一个可以被另两个连续段的交/并表示出来的连续段显然是废的。这样的话，我们可以定义本原连续段\(M\)表示一个连续段，满足在\(I_P\)中，不存在与\(M\)相交且互不包含的连续段。
那又有一个性质：一个连续段可以由几个本原连续段构成。这样一来，本原连续段的集合\(M_P\)就是\(I_P\)的一个极小基（即不存在比它更小却能表示出\(I_P\)的集合）。

析合树
终于说到析合树了。
事实上，我们可以把\(I_P\)映射到一棵有根树上，并且这个映射是一个双射，我们称这棵有根树为析合树。具体地说，析合树的每个节点表示一个本原连续段，点\(i\)是点\(j\)的祖先当且仅当段\(M_j\subsetneq\)段\(M_i\)。该树的每个节点分为析点和合点两种：
析点：将所有子节点的值域区间离散化形成一个区间（暂且称之为儿子排列），儿子排列中的每一个非平凡区间（即1<长度<子节点个数），均不是连续段。
合点：……，均是连续段。
盗张图来表示一下。
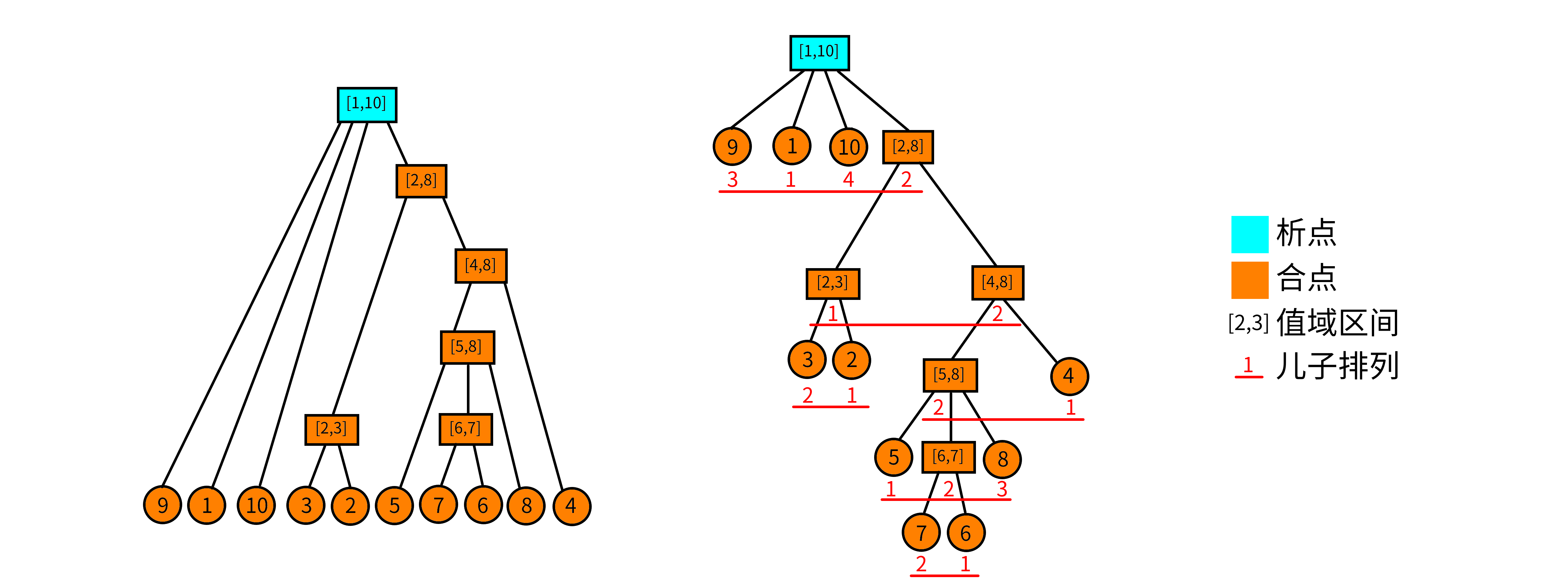
析点和合点也有一些显然的性质：对于非叶节点，合点至少有两个儿子，析点至少有四个……

构造
这里我讲的是一种\(O(n)\)的增量法。
假设现在已经搞定了[1…i-1]的析和森林，我们把每个析合树的root拿出来放到一个栈里（代表区间后的在栈顶）。现在，要加入第i个位置，先建一个析点就表示这个位置，设为x。
考虑如何加入一个点。

设要加入的点是x，栈顶的点是y。
有三种情况：

y是一个合点，x能成为y新的儿子（即\(ran(y的最后一个儿子)\)和\(ran(x)\)连接起来是连续段），拿y递归加入。
若1不可，而y和x能成为兄弟（即\(ran(y)\)和\(ran(x)\)连接起来是连续段），新生成一个点z，作为y和x共有合点父亲，拿z递归加入。
若1、2都不可，新生成一个点z，作为x和栈顶的若干点（尽量少）的共有析点父亲，拿z递归加入。
若1、2、3都不可，说明不能再合并什么的了，直接把x加入栈顶。

情况1、2、4都很简单，关键就在于处理情况3。

由于情况3是生成一个析点z，故其任意两个相邻儿子的值域区间都不能连起来；而我们又要保证z代表了一个连续段。
设我们现在加入的点x表示的区间是\([x_x,y]\)，则点z的区间是\([x_z,y]\)。我们求出\(a_i\in ran(z)\)的\(i\)的最小值\(l\)和最大值\(r\)，这能形成一个区间\([l,r]\)。显然，当\(r>y\)时，不论我们怎么扩展\(x_z\)，z都不可能是一个连续段；那这样一来，只有当\(r≤y\)并且点z尚不为连续段时，我们才合并栈顶。
具体实现时，我们可以先通过RMQ、线段树之类的东西预处理每个区间\([i,i+1]\)所对应的\([l,r]\)，然后对于每个点x（设它表示区间\([i,j]\)）额外记录两个区间\([l_c,r_c]\)、\([l_d,r_d]\)分别表示区间\([i,j+1]\)、区间\([i,j]\)各自对应的\([l,r]\)。这个可以由我们预处理出的东西合并得来。

但是上述做法在最坏情况下要遍历整个栈，渐进复杂度是\(O(n^2)\)的。
考虑优化。我们可以给每个通过操作4压入栈的点维护一个类似fail指针：\(L_i\)表示从\(i\)出发直接和间接地向左最远能到达的位置（即满足\((L_i,i]\)是一个连续段的最小的数）。那显然就是进行操作3尝试合并失败，第一次\(r>y\)时的栈顶值。当然，除了这个，我们还要将构造不成功的点z记录下来。
这样一来，我们处理情况3时，就不用遍历栈，而是可以沿着栈顶的fail链跑，每次把将被合并的点改为当时的z。因为\((L_i,i]\)都是左开右闭的区间，并起来还是左开右闭的区间，故正确性十分显然。
然后又由于走过的\(L_i\)不会再走了，故而构造的时间复杂度是\(O(n)\)的。

板题
GMOJ6202=GMOJ6279
这两道题都是求包含询问区间的最小连续段，那么就是在析合树上找LCA，假如找到的是析点则直接取析点；不然的话，要从合点LCA下移一步走到两个点，然后取两个点的并（因为合点可能包括了其他不在询问范围内的本原连续段）。

Code

#include <cstdio>
#include <algorithm>
#define A v*2
#define B A+1
#define min(x,y) (x<y?x:y)
#define max(x,y) (x>y?x:y)
#define MIN(x,y) if(x>y)x=y
#define MAX(x,y) if(x<y)x=y
#define fo(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
using namespace std;

const int N=233333;
int n,a[N],pos[N],t0[N*4],t1[N*4],pl,pr,id[N];

void bt(int v,int l,int r)
{
    if(l==r) {t0[v]=t1[v]=pos[l]; return;}
    int m=l+r>>1;
    bt(A,l,m), bt(B,m+1,r);
    t0[v]=min(t0[A],t0[B]);
    t1[v]=max(t1[A],t1[B]);
}

struct P
{
    int x,y;
    inline P(){x=N,y=0;}
    inline P(int _x,int _y){x=_x,y=_y;}
};
inline void uni(P&a,const P&b) {MIN(a.x,b.x); MAX(a.y,b.y);}
struct nod
{
    bool dv;
    int ls;
    P a,b,c,d;
}b[N]; int b0;
void ft(int v,int l,int r)
{
    if(pr< l||r< pl) return;
    if(pl<=l&&r<=pr) {MIN(b[b0].c.x,t0[v]); MAX(b[b0].c.y,t1[v]); return;}
    int m=l+r>>1;
    ft(A,l,m), ft(B,m+1,r);
}

inline bool ck(nod a) {return a.a.y-a.a.x==a.b.y-a.b.x;}
inline nod uni(nod a,nod b) 
{
    uni(a.a,b.a), uni(a.b,b.b);
    a.d=a.c, uni(a.d,b.d);
    uni(a.c,b.c);
    return a;
}
int z[N],z0,f[N][17],r[N],q0,q[N],dep[N];
struct fail{int x; nod a;}d[N];
int add(int x)
{
    if(!z0) {z[++z0]=x; return 0;}
    int y=z[z0];
    if(!b[y].dv&&ck(uni(b[b[y].ls],b[x])))
    {
        b[y]=uni(b[y],b[x]), z0--;
        return f[b[y].ls=x][0]=y;
    }
    if(ck(uni(b[y],b[x])))
    {
        b[++b0]=uni(b[y],b[x]), z0--;
        b[b0].ls=x, b[b0].dv=0;
        return f[y][0]=f[x][0]=b0;
    }
    int t=z0;
    nod e=uni(b[y],b[x]);
    for(; e.d.y<=b[x].a.y&&!ck(e); t=d[t].x) e=uni(d[t].a,e);
    if(ck(e))
    {
        b[++b0]=e, b[b0].dv=1, b[b0].ls=z[++z0]=x;
        fo(i,t,z0) f[z[i]][0]=b0;
        z0=t-1;
        return b0;
    }
    z[++z0]=x;
    d[z0]=(fail){t,e};
    return 0;
}

int lca(int x,int y)
{
    if(dep[x]<dep[y]) swap(x,y);
    fd(i,16,0) if(dep[f[x][i]]>=dep[y]) x=f[x][i];
    if(x==y) return x;
    fd(i,16,0) if(f[x][i]^f[y][i]) x=f[x][i],y=f[y][i];
    return f[x][0];
}

int go(int x,int y)
{
    fd(i,16,0) if(dep[f[y][i]]>dep[x]) y=f[y][i];
    return y;
}

int m,x,y;
int main()
{
    freopen("sequence.in","r",stdin);
    freopen("sequence.out","w",stdout);
    scanf("%d",&n);
    fo(i,1,n) scanf("%d",&a[i]), pos[a[i]]=i;
    bt(1,1,n);
    fo(i,1,n)
    {
        b[id[i]=++b0].dv=1;
        b[b0].a=P(i,i);
        b[b0].b=P(a[i],a[i]);
        b[b0].c=b[b0].d=P();
        if(i<n)
        {
            pl=a[i], pr=a[i+1];
            if(pl>pr) swap(pl,pr);
            ft(1,1,n);
        }
        for(x=b0; x; x=add(x));
    }
    fo(i,1,b0) r[f[i][0]]++;
    fo(i,1,b0) if(!r[i]) q[++q0]=i;
    fo(i,1,q0)
    {
        x=q[i];
        if(f[x][0]&&!--r[f[x][0]]) q[++q0]=f[x][0];
    }
    fd(i,q0,1)
    {
        x=q[i];
        dep[x]=dep[f[x][0]]+1;
        fo(j,1,16) f[x][j]=f[f[x][j-1]][j-1];
    }
    for(scanf("%d",&m); m--;)
    {
        scanf("%d%d",&x,&y);
        int z=lca(id[x],id[y]);
        nod w=b[z].dv ? b[z] : uni(b[go(z,id[x])],b[go(z,id[y])]);
        printf("%d %d\n",w.a.x,w.a.y);
    }
}