标签:整数 div 输入格式 namespace cout ons mes class for
如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出orz
第一行包含两个整数N、M,表示该图共有N个结点和M条无向边。(N<=5000,M<=200000)
接下来M行每行包含三个整数Xi、Yi、Zi,表示有一条长度为Zi的无向边连接结点Xi、Yi
输出包含一个数,即最小生成树的各边的长度之和;如果该图不连通则输出orz
4 5 1 2 2 1 3 2 1 4 3 2 3 4 3 4 3
7
时空限制:1000ms,128M
数据规模:
对于20%的数据:N<=5,M<=20
对于40%的数据:N<=50,M<=2500
对于70%的数据:N<=500,M<=10000
对于100%的数据:N<=5000,M<=200000
样例解释:
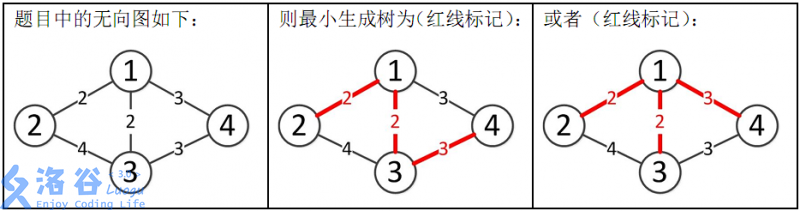
所以最小生成树的总边权为2+2+3=7
AC代码兼模板
#include <bits/stdc++.h> using namespace std; const int NN = 1e4+10; int N,M; int fa[NN]; struct node{ int a,b,w; friend bool operator < (node n1,node n2){ //node结构体的排序规则,不想定义cmp,毕竟多写一个函数 return n1.w < n2.w; } }; vector<node> ve; //存放边的容器 int find(int x){ //查找祖先 if(x!=fa[x]) fa[x] = find(fa[x]); return fa[x]; } void join(int x,int y){ //合并 int fx = find(x),fy = find(y); if(fx!=fy) fa[fx] = fy; } int main(){ cin>>N>>M; for(int i = 1;i<=N;i++) fa[i] = i; int a,b,w; while(M--){ scanf("%d%d%d",&a,&b,&w); ve.push_back({a,b,w}); } sort(ve.begin(),ve.end());//排序 long long sum = 0; //构图的所有边总长度 int edges = 0; //选边数 for(auto v:ve){ if(find(v.a) != find(v.b)){ //如果a点与b点没有联通,就选此边进行合并 join(v.a,v.b); sum+=v.w; edges++; } } if(edges >= N-1) cout<<sum<<endl; else cout<<"orz"<<endl; return 0; }
标签:整数 div 输入格式 namespace cout ons mes class for
原文地址:https://www.cnblogs.com/bigbrox/p/11311887.html