标签:高度 表示 info 去除 mil 存在 之间 放松 强制
状压DP
状态压缩dp
状态压缩是设计dp状态的一种方式。
当普通的dp状态维数很多(或者说维数与输入数据有关),但每一维总量很少时,可以将多维状态压缩为一维来记录。
这种题目最明显的特征就是:都存在某一给定信息的范围非常小(在20以内),而我们在dp中所谓压缩的就是这一信息。
(或者是在做题过程中分析出了某一信息种类数很少)
我们来看个例子。
经典题
?给出一个n*m的棋盘,要放上一些棋子,要求不能有任意两个棋子相邻。求方案数。
? n<=100;
?m<=8。
如果m固定的话可以设f[i][0/1][0/1]...[0/1]表示每一行每一列放不放
如果不是固定的呢?
我们发现后面的多个0/1可以看成一个二进制数
那我们不就可以用数字代替后面的维数吗?
f[i][s]->f[i+1][s’](s&s’==0)
你会发现这样记录很暴力,状态数是与m相关的指数级的,但同时也就是因为m小我们就确实可以这么做。
其实本质就是很暴力的记录状态,只不过利用了题目本身的特殊条件(这一维很小),使得我们并不会因此复杂度过高。
同时也就是说,如果题目本身没有这样一个较小的信息,就不能应用状态压缩。
所以在接下来的题目中大家可以更注意一下题目所给的条件。
状态压缩dp肯定是有一维是指数级的,这正是状态压缩的特点。
BZOJ1087 互不侵犯
在n*n的棋盘上放置k个国王,使得任意两个国王互相不攻击。一个国王可以攻击到周围八个格子。
求放置方案数。
n<=9
f[i][j][s]第i行,已经放了j个国王,当前状态是s
枚举s’
-->f[i+1][j+bit(s)][s’]
为了判断,我们可以向左移或者右移再判断
(T|(T<<1)|(T>>1)) & S==0就可以转移了
位运算
1、(s & (1 << i)):判断第 i 位是否是 1;
2、s =s|(1<<i):把第 i 位设置成 1;
3、s =s&(~(1<<i)):把第 i 位设置成 0;
(~:是按位取反,包括符号位)
4、s =s^(1<<i) :把第 i 位的值取反;
5、s =s & (s – 1):把一个数字 s 二进制下最靠右的第一个 1 去掉;
6、for (s0 = s; s0; s0 = (s0 - 1) & s): 依次枚举 s 的子集;(从大到小)

它的复杂度是3^n
n表示位数,k表示有几个1
ΣC(k,n)*2^k*1^(n-k) (k=0~n)
不就是二项式定理吗
7: x&-x 取出x最低位的1。
拓扑序个数问题
给你一张拓扑图,求这张拓扑图有多少种不同的拓扑序.
n<=20。
dp[s]表示选了集合s中的数的拓扑序数量
时间复杂度:2^n*n*判断是否成立
如何快速判断?
设in[u]=s表示所有能到达u的点的集合
s&in[u]=in[u]
bzoj2734
给定n,问集合{1,2,3,…,n}有多少个子集满足:若x在集合内,则2x和3x不在集合内。
n<=100000
每一个数可以看成q* 2^x * 3^x
如果不看q(把q相同的提出来)
 相邻两个数
相邻两个数
假设一列一列来
s要记到这一行的数的个数,即2^16
转移的时候到下一行,可能到2^15
乘起来就比较大了
毕竟斐波那契数列的第31项
一行一行呢?
一共11个数
下一行是10
斐波那契数列的第21个数就可以接受了
dp[i][s]表示到了第i层(按照行和斜杠)
看看s’&s是否=0
如果是就转移
记g[x]表示将x中的2,3因子去除后得到的值,若g[x]!=g[y],那么x与y互不影响。对于互相有影响的一组数,一定能表示成q*2^a*3^b(q为常数)。对每种q分别求解,再相乘即可。
以q=1为例,可把所有2^a*3^b以a,b为行列画成一个三角形棋盘,求棋盘上放不能相邻的棋子的方案数。我们会发现这个三角形最宽的层最多只有11个,所以可以状态压缩。
当q>1,等价于q‘=1&&n‘=n/q。
剪枝:对于n/q相同的q,可以避免重复计算来加速。
打个表
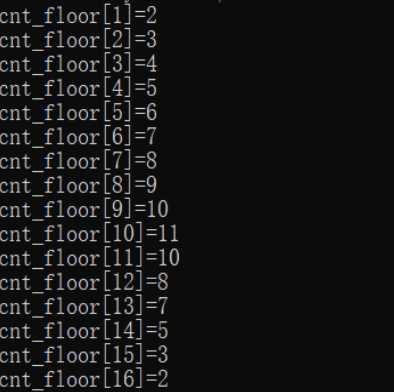
我们看到最宽的一层第10层宽度只有11,这个范围显然是可以2^cnt_floor状态压缩。
NOIP2016 愤怒的小鸟
平面上有n头猪,每次可以从(0,0)出发发射一只沿抛物线(y=ax^2+bx)飞行的小鸟,可以消灭所有在飞行路线上的猪。
问消灭所有猪至少要几只小鸟。
n<=18
某一些猪的集合是可以一起消灭的
选出最少的集合
两个点确定一条抛物线
抛物线的数量n^2
dp[s]表示集合s的猪全部消灭最少需要多少抛物线
t[i]表示抛物线消灭的猪的集合
枚举s中最小的点被那一条抛物线经过
dp[s]=min{dp[s^t[i]+1|t[i]&s=t[i],t[i]包含s最低位}
复杂度2^n *n,因为已经确定一个点,只需要枚举另一个点就行了
poj2923
有 n 个货物,并且知道了每个货物的重量,每次用载重量分别为c1,c2的火车装载,问最少需要运送多少次可以将货物运完。
N<=17
如果处理出来了那些集合t可以通过一次操作运走,那这个题就和上一个差不多了
dp[s]=min{dp[s^t]+1|t&s==t}
3^n
先判断被一辆车运走
f表示第一辆车,g表示第二辆车
t[s]=| (f[s’]&g[s^s’])
3^n
强制t包含s最低位,可以稍微提高一下速度
Bzoj3900
动物园里有 n 头麋鹿。每头麋鹿有两支茸角,每支茸角有一个重量。然而,一旦某头麋鹿上两支茸角的重量之差过大,这头麋鹿就会失去平衡摔倒。为了不然这种悲剧发生,动物园院长决定交换某些茸角,使得任意一头麋鹿的两角重量差不超过 c。然而,交换两支茸角十分麻烦,不仅因为茸角需要多个人来搬运,而且会给麋鹿造成痛苦。因此,你需要计算出最少交换次数,使得任意一头麋鹿的两角重量差不超过 c。
-注意,交换两支茸角只能在两头麋鹿之间进行。因为交换同一头麋鹿的两支角是没有意义的。
对于 100% 的数据,n <= 16, c <= 1000000, 每支茸角重量不超过 1000000。
先看看有没有解
先排序,然后两两结合判断是否差在c之内
最多需要交换t-1次
因为每次操作至少使一个变成合法的
f[s]=cnt(s)-1
f[s]还有可能更小
我们希望把整个集合分成很多更小的集合使得每一个集合都可以通过cnt(s’)-1次交换达到要求
f[s]=min{f[s’]+f[s^s’]|s’∈s}
g[s]=[]表示s集合排完序的数组
原来的做法2^n*n*logn+3^n
g[s]相当于g[s^(i<<i)]加两个角
2^n*n+3^n
Hdu3001放松题
现在有一个具有n个顶点和m条边的无向图(每条边都有一个距离权值),小明可以从任意的顶点出发,他想走过所有的顶点而且要求走的总距离最小,并且他要求过程中走过任何一个点的次数不超过2次。
? 1<=n<=10
三进制状压
再记一维当前在哪一位上
len[u][v]
dp[s][u]--------->dp[s+(1<<1)][v]
min(dp[s][1~n])
复杂度3^n*n*n
关于时间复杂度
N=20一般是2^n或者n*2^n。
N<=16大概率是3^n,约是4*10^7,那很可能做法就和之前讲枚举子集有关了。
N<=15大概率是3^n或者n*3^n。
BZOJ3717 Pakowanie
给出n个物品和m个包,物品有各自的体积,包有各自的容量。
问将所有物品装入包中需要至少几个包。
n<=24,m<=100。
先把包从大到小排序
每次考虑s集合多选进来是否需要多加一个包
f[s]表示s集合最少需要多少包
g[s]表示在f的情况下最后一个包剩下多少空间
转移时枚举放哪个就行
基本的状态压缩dp。
Ø位运算在状压dp中,经常能发挥大的作用,灵活的使用位运算可以降
低算法的时间复杂度。
Ø选择一些不相交的可行集合并起来等于全集,且希望选出集合总权值
尽量大,通常要O(3^n)枚举子集的技巧。而通过强制枚举的子集包含
最低位的1,可以避免重复的计算。
Ø通过一个类TSP问题,对三进制状态压缩的初探。
noip范围内的dp优化方法
加速状态转移:
1:前缀和优化
2:单调队列优化
3:树状数组或线段树优化
精简状态
3:精简状态往往是通过对题目本身性质的分析,去省掉一些冗余的状态。相对以上三条套路性更少,对分析能力的要求更高。
前缀和优化
逆序对
求长度为n,逆序对为k的排列有多少个,答案对10^9+7取模。
1<=N,K<=200
1<=N,K<=2000
dp[i][j]表示前i个数产生j个逆序对
插进第i个数时,在最后会产生0个逆序对,倒数第二个位置会产生1个逆序对...放最前面会产生i-1个逆序对
发现它是一个连续的段
dp[i][j]=Σdp[i-1][j-k](k=1~i-1)
我们设:
则dp[i][j]=f[i-1][j]-f[i-1][j-i]
这样我们通过记录前缀和,将转移优化成O(1)
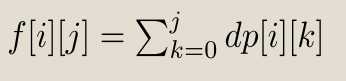
O(n*k)
单调队列
基本形式,适用范围
单调队列维护dp,一般就是把一个O(N)转移的dp通过单调队列优化成一个均摊O(1)转移的式子。
式子形如:dp[i]=max{f(j) }+g[i](这里的g[i]是与j无关的量),且j的取值是一段连续区间,区间端点的两端随着i增大而增大的区间。
(同时如果这个可行的区间左端点固定,我们就可以通过之前讲的记录前缀最小值来处理)
这里的f(j)是仅和j有关的项。以下是常见的一维和二维的情况。
dp[i]=max{dp[j]+f(j)}+g[i] 或者 dp[level][i]=max{dp[level-1][j]+f(j)}+g(i)
这样的题我们就可以做单调队列优化。
bzoj1855: 股票交易
我们考虑在未来T天内的某只股票,第i天的买入价为每股APi,第i天的卖出价为每股BPi(对于每个i,都有APi>=BPi),每天不能无限制地交易,
规定第i天至多只能购买ASi股,至多卖出BSi股。另外规定在两次交易(买入或者卖出均算交易)之间,至少要间隔W天,也就是说如果在第i天发生了交易,那么从第i+1天到第i+W天,均不能发生交易。还规定在任何时间,一个人的手里的股票数不能超过MaxP。
初始w手里有一大笔钱(可以认为钱的数目无限),但是没有任何股票,
问T天以后,小w最多能赚多少钱。
0<=W<T<=2000
单调队列优化和前缀和优化的对比
单调队列优化dp跟前缀和优化dp差不多一个思路,转移的合法点集都是一个区间。
只不过,单调队列优化dp是当你在最优化dp值时候和一段区间有关。
而前缀和优化dp是在计数的时候和一段区间有关
bzoj3831: [Poi2014]Little Bird
有一排n棵树,第i棵树的高度是Di。
MHY要从第一棵树到第n棵树去找他的妹子玩。
如果MHY在第i棵树,那么他可以跳到第i+1,i+2,...,i+k棵树。
如果MHY跳到一棵不矮于当前树的树,那么他的劳累值会+1,否则不会。
为了有体力和妹子玩,MHY要最小化劳累值。
N(2<=N<=1 000 000)
f[i]表示跳到第i棵树的最小劳累值
劳累值只增加1
单调队列按照dp值小的存
如果dp值相同就选高的
根据题意,我们很容易得出下面的转移方程
1.f[i]=min(f[j]+1) ( i-k≤j<i)
2.f[i]=min(f[j]) ( i-k≤j<i&&h[j]>h[i])
发现上面那个东西用单调队列直接搞定,但下面那个不太好搞。不过发现由于h[j]>h[i]对答案的贡献至多为1,所以原来如果f[j]<f[j‘],那么算上h[j]和h[j’]的影响后j仍然不会比j‘更差,于是直接维护一个f递增的单调队列,
其中当f相同的时候使h递减就行了。
这么做,主要利用了题目中高和矮转移的费用只差1,这样如果矮的f[i]小的话,就算加上1也只是和高的f值相同不会更差。如果费用更高就不能用这个方法了。
树状数组或线段树优化
送你一堆区间
送你在数轴上的 n 个区间和 m 个关键点, 可以决定每个区间选或不选,问有多少种方案覆盖 所有的关键点.
对 1000000009 取模.
N<=5*10^5
左端点排序
dp[i][j]表示到了前i条线段,覆盖完前j个位置的方案数

单点赋值,区间乘二,求前缀和
线段树
Noip2008传纸条
一个m行n列的矩阵,而小渊和小轩传纸条。纸条从小渊坐标(1,1),传到小轩坐标(m,n)。从小渊传到小轩的纸条只可以向下或者向右传递,从小轩传给小渊的纸条只可以向上或者向左传递。
班里每个同学都可以帮他们传递,但只会帮他们一次。
全班每个同学有一个好心程度。小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条,即找到来回两条传递路径,使得这两条路径上同学的好心程度之和最大。
? n,m<=300。
其实可以理解为从小渊到小轩传两次。
最暴力的做法:设dp[i][j][k][l]是第一张纸条到达(i,j),第二张到达(k,l)时最大权值。那么方程就是
dp[i][j][k][l] = map[i][j] + map[k][l] + max(dp[i - 1][j][k - 1][l],dp[i -1][j][k][l -1],dp[i][j - 1][k -1][l],dp[i][j -1][k][l -1]);
还有一点注意的是,如果i == k && j == l,也就是第二张走了第一张的路径,那么就要减去,dp[i][j][k][l] -= map[i][j];
接下来枚举每个i,j,k,l,最后输出dp[m][n][m][n]就行了,但这样做时间复杂度是O(n^4),
其实我们可以让两个路线并行走,同时走。
而既然第一张与第二张是同时走,那么我们知道他们的步数是一样的,步数 = 横坐标+纵坐标,所以只需枚举i,j,k,就能计算出l,只需三重循环,时间就变成了O(n^3);
dp[i][j][k] = map[i][j] + map[k][i+j-k] + max(dp[i - 1][j][k - 1],dp[i -1][j][k],dp[i][j- 1][k -1],dp[i][j -1][k]);
标签:高度 表示 info 去除 mil 存在 之间 放松 强制
原文地址:https://www.cnblogs.com/lcezych/p/11323527.html