标签:getch print space find lca 核心 for set +=

午时刷题,难甚,遂小憩于桌上,惊醒,于梦中有所得,虽大声曰:吾已得tarjan之奥秘!
关于tarjan算法,其实就是一个递归加并查集的应用。
大致代码:
#include<bits/stdc++.h> using namespace std; int find(int x){ .... } void join(int x,int y) { .... } void dfs(int x) { int len=v[x].size(); for(int i=0; i<len; i++) //遍历x的子节点 { dfs(v[x][i]); //继续往下推 join(v[x][i],x); //将x的所有子节点的祖先都设为x } vis[x] = true; //证明x走过了 for(int i=1; i<=n; i++) //对每个x循环1~n if(vis[i]&&g[x][i]) //如果i已经走过并且要求(x,i) ans=find(i); //lca就是ans }
由以上代码可以看出,tarjan实际上就是并查集与dfs的结合,其最核心的部分就是dfs那部分
只要理解了dfs()的内容,就能理解tarjan
而对于dfs函数,我们首先就会想到它的特性:不撞南墙不回头。
假如有一颗树,对其dfs,那么首先它会沿着一个分支一直到尽头(如图):
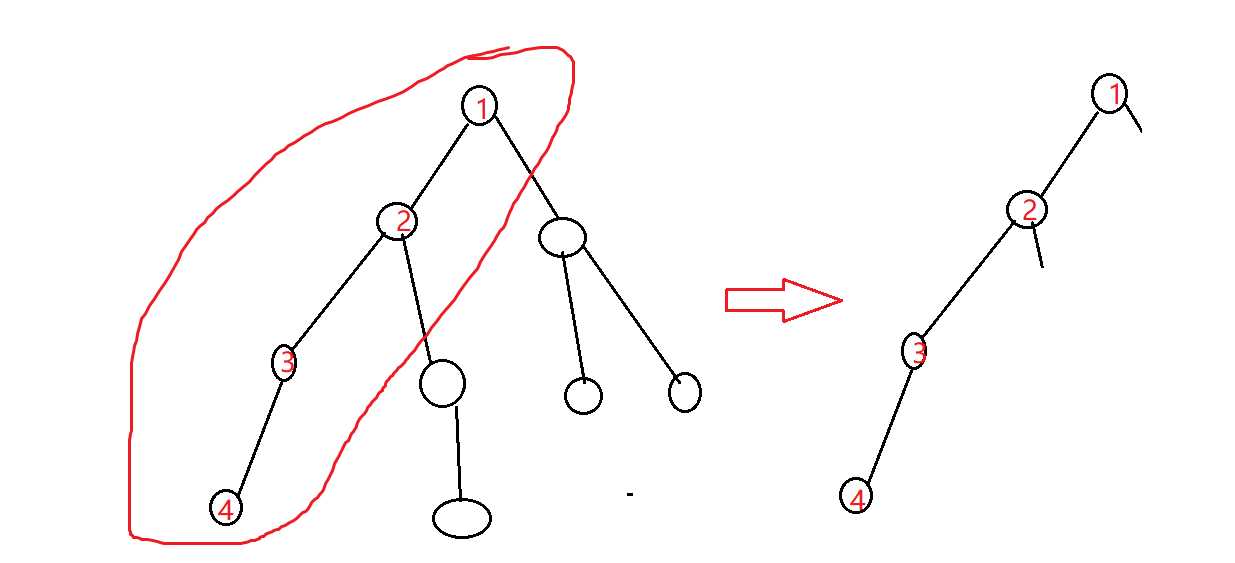
而当走到4这个点时,函数开始执行下列语句:
join(v[x][i],x); //将x的所有子节点的祖先都设为x
//而此时pre[4]=3;pre[3]=3;pre[2]=2;pre[1]=1;
再然后是:
vis[x] = true; //证明x走过了 for(int i=1; i<=n; i++) //对每个x循环1~n if(vis[i]&&g[x][i]) //如果i已经走过并且要求(x,i) ans=find(i); //lca就是ans }
如果存在要求lca[x][i],先看i点是否走过,如果走过,那就只有一种可能(真相只有一个!真実はいつも一つ):
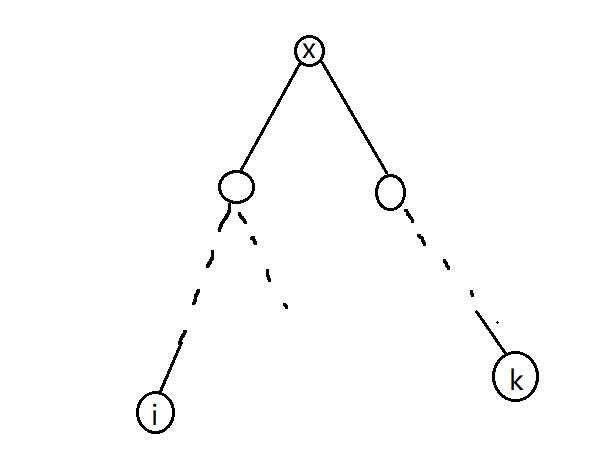
i,k必在两条不同分支上,并且交于某个点x,如果i已经走过了,那么,i所在的这条分支上所有的点都有明确的父子关系,即find(i)==x!
代码参上:
#pragma GCC optimize(2) #include<stdio.h> #include<string.h> #include<vector> #define M 1007 using namespace std; int g[M][M],in[M],pre[M],cnt[M]; bool vis[M]; vector<int>v[M]; int n,m; void init() { memset(g,0,sizeof(g)); memset(in,0,sizeof(in)); memset(cnt,0,sizeof(cnt)); memset(vis,false,sizeof(vis)); for(int i=1; i<=n; i++) { v[i].clear(); pre[i]=i; } } int fond(int x) { return x==pre[x]?x:pre[x]=fond(pre[x]); } void join(int x,int y) { int xx=fond(x); int yy=fond(y); pre[xx]=yy; } void dfs(int x) { int len=v[x].size(); for(int i=0; i<len; i++) //遍历x的子节点 { dfs(v[x][i]); //继续往下推 join(v[x][i],x); //将x的所有子节点的祖先都设为x } vis[x] = true; //证明x走过了 for(int i=1; i<=n; i++) //对每个x循环1~n if(vis[i]&&g[x][i]) //如果i已经走过并且要求(x,i) cnt[fond(i)]+=g[x][i]; // } int main() { while(scanf("%d",&n)!=EOF) { init(); int a,b,c,root; for(int i=1; i<=n; i++) { scanf("%d:(%d)",&a,&b); while(b--) { scanf(" %d",&c); v[a].push_back(c); in[c]++; } } scanf("%d",&m); getchar(); while(m--) { scanf("(%d,%d)",&a,&b); getchar(); g[a][b]++; g[b][a]++; } for(int i=1; i<=n; i++) if(!in[i]) { root=i; break; } dfs(root); for(int i=1; i<=n; i++) { if(cnt[i]) printf("%d\n",i); } } return 0; }
以上;
Closest Common Ancestors (Lca,tarjan)
标签:getch print space find lca 核心 for set +=
原文地址:https://www.cnblogs.com/zjydeoneday/p/lca.html