标签：call   art   mamicode   arc   some   which   tom   tree   image   

First lets recall the concept for BFS and DFS.

I will use below Binary Tree as an example. 

Before that, lets go through some of the concepts of Trees and Binary Trees quickly. 

Concept of Binary Trees

A binary tree is made of nodes, where each node contains a "left" reference, a "right" reference, and a data element. The topmost node in the tree is called the root.

More tree terminology:

• The depth of a node is the number of edges from the root to the node.
  
• The height of a node is the number of edges from the node to the deepest leaf.
• The height of a tree is a height of the root.

Concept of Binary search Tree.

Binary Search Trees

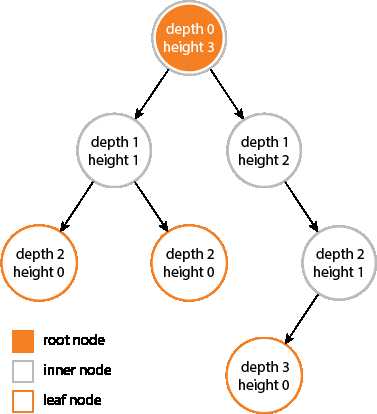
We consider a particular kind of a binary tree called a Binary Search Tree (BST). The basic idea behind this data structure is to have such a storing repository that provides the efficient way of data sorting, searching and retriving.

A BST is a binary tree where nodes are ordered in the following way: each node contains one key (also known as data) the keys in the left subtree are less then the key in its parent node, in short L < P; the keys in the right subtree are greater the key in its parent node, in short P < R; duplicate keys are not allowed. In the following tree all nodes in the left subtree of 10 have keys < 10 while all nodes in the right subtree > 10. Because both the left and right subtrees of a BST are again search trees; the above definition is recursively applied to all internal nodes:

Traversals

Traversal is the process that visits all the nodes in a tree. Since a tree is a non-linear data structure, there is no unique traversal. We will consider several traversal algorithms which we group in the following two kinds.

• Depth-first traversal.
• Breadth-first traversal.

 There are three different types of depth-first traversals, :

• PreOrder traversal :  Visit Parent First, then left child, and then right child. 
• InOrder traversal　:  Visit Left Child, then Parent, then Right child
• PostOrder traversal:  visit left child, then the right child and then the parent;

There is only one kind of breadth-first traversal--t

• the level order traversal. This traversal visits nodes by levels from top to bottom and from left to right.

Example.

for below tree: 

 PreOrder traversal 8 ->5->9->7->1->12->2->4->11->3

 InOrder traversal   9-> 5->1->7->2->12->8->4->3->11

PostOrder Traversal  9->1->2->12->7->5->3->11->4->8   

Level Order  8->5->4->9->7->11->1->12->3->2

Binary Search Tree Insertion

The insertion procedure is quite similar to searching.

We start at the root and recursively go down the tree searching for a location in a BST to insert a new node.

If the element to be inserted is already in the tree, we are done (we do not insert duplicates).

The new node will always replace a NULL reference.

Exercise

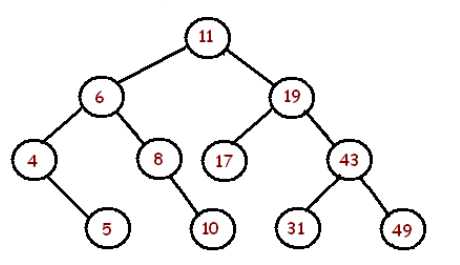
Exercise. Given a sequence of numbers:

11, 6, 8, 19, 4, 10, 5, 17, 43, 49, 31

Draw a binary search tree by inserting the above numbers from left to right.

(answer to below)

Searching

Searching in a BST always starts at the root. We compare a data stored at the root with the key we are searching for (let us call it as toSearch). If the node does not contain the key we proceed either to the left or right child depending upon comparison. If the result of comparison is negative we go to the left child, otherwise - to the right child. The recursive structure of a BST yields a recursive algorithm.

Please refer to below link to for "Deletion in Binary Search Tree";

https://www.cs.cmu.edu/~adamchik/15-121/lectures/Trees/trees.html

Breadth First Search VS Depth First Search (Algorithms)

标签：call   art   mamicode   arc   some   which   tom   tree   image   

原文地址：https://www.cnblogs.com/codingyangmao/p/11328344.html