标签：lvg   bom   AAT   srx   div   vss   aws   apm   epp   

题目描述

SarvaTathagata是个神仙，一天他在研究数论时，书上有这么一个问题：求不超过n两两的数的gcd。
SarvaTathagata这么神仙的人当然觉得这个是sb题啦。学习之余，他还发现gcd的某一个特别好的性质：如果有两个数i,j满足gcd(i,j)=i^j(这里的^为c++中的异或)的话，那么这两个数组成的数对(i,j)就是一个nb的数对(这里认为(i,j)和(j,i)为相同的，并不需要计算2次)。
当然，SarvaTathagata并不会只满足于判断一个数对是否nb，他还想知道满足两个数都是不超过n并且nb的数对有多少个。
由于SarvaTathagata实在是太神仙了，他认为这种题实在是太简单了。于是他找到了你，看看你是否能解决这个问题。

 

输入

共一行一个整数n，含义如题所述。

输出

一行一个整数，表示nb的数对的个数。

 

样例输入

样例输入1
12
样例输入2
123456

样例输出

样例输出1
8
样例输出2
214394

 

数据范围限制

 

提示

样例1中共有八对，分别是： {1,3},{1,5},{1,7},{1,9},{2,6},{1,11},{2,10},{4,12}。

题解：

首先我们看到这一道题，聪明的你一定发现了第10个点：n<=20000000。

但是，先不要慌，我们先来证一个不等式：

证明：x ^ y >= x - y >= gcd( x , y )。（其中‘^’代表异或）

我们先来证明左边。

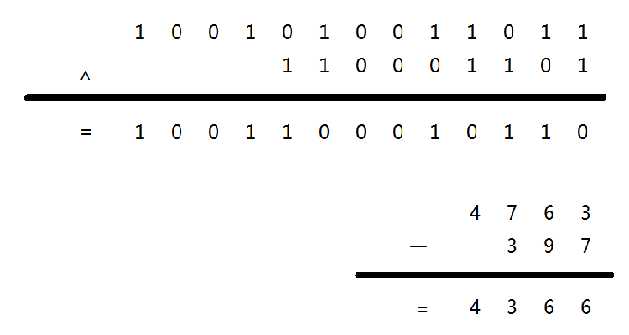
从上面那一张异或与减运算的竖式中可以看出：

其实"^"和"-"运算唯一不同的地方仅仅在于运算方法上的不同。

所以我们不妨将上图中所有的数都转化成二进制。

于是就有：

这时候我们注意一下下图中圈了红圈的地方：

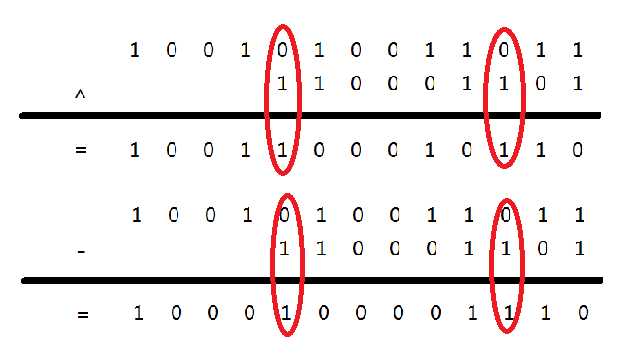
我们可以发现：当a=0，b=1时，a异或b=1，而a-b=-1（图中具体表现为退位）。

为了让你更好的理解，下面请看一张分析表：

 所以，我们可知，对于两个数的对应的每一位a，b，均有：

a xor b >= a - b 。（xor表示异或）

所以 x xor y >= x - y ，当且仅当x与y的对应二进制位不为0和1时，等号成立。

原式左边得证。

下面我们再看到右边：x - y >= gcd( x , y )。

根据更相减损术：gcd( x , y )=gcd( y , x-y )，( x > y )

(没有听过更相减损术的人可以点击这里）

所以原式等价于x - y >=gcd( y , x-y )。

又因为b = gcd( a , b ) * k (k >= 1)，

所以x - y >=gcd( y , x-y )这个式子显然成立。

原式右边得证。

所以原式得证。

现在我们回到原题，题目的条件为：

i xor j = gcd( i , j )。

我们将它带人那个不等式中，可得：

i xor j = i - j = gcd( i , j )。

也就是说，i - j = i xor j。

 所以我们只要枚举i与i xor j就行了。

代码：

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 int n,sum;
 4 int main()
 5 {
 6     cin>>n;
 7     for(int c=1;c<=n;c++)//枚举a-b（同时也是gcd(a,b)） 
 8     for(int a=2*c;a<=n;a+=c)//因为a>=b，所以从a=2*c开始枚举 
 9     if(c==(a ^ a-c))sum++;//如果 c=a^b（b=a-c），答案++ 
10     printf("%d",sum);//输出答案 
11     return 0;
12 }

可是，n<=20000000啊！

没事，不慌。

相信我。

你们知道微积分吗？

如果不知道，我现场告诉你一个公式：

n/1+n/2+n/3+……+n/n=log_en (因为本人是初中蒟蒻，所以只知道有这东西)

你知道这意味着什么吗？

我们的程序的时间复杂度其实是nlog_en=nlog_n！

所以……可以AC！

（本人的温馨提示：建议大家最好像上面的代码一样，不然会被卡常！）

妙！

2298. 异或

标签：lvg   bom   AAT   srx   div   vss   aws   apm   epp   

原文地址：https://www.cnblogs.com/xinxiyuan/p/11327973.html